8.3: Volatilization Gravimetry
- Page ID
- 220727
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)A second approach to gravimetry is to thermally or chemically decompose the sample and measure the resulting change in its mass. Alternatively, we can trap and weigh a volatile decomposition product. Because the release of a volatile species is an essential part of these methods, we classify them collectively as volatilization gravimetric methods of analysis.
Theory and Practice
Whether an analysis is direct or indirect, volatilization gravimetry usually requires that we know the products of the decomposition reaction. This rarely is a problem for organic compounds, which typically decompose to form simple gases such as CO2, H2O, and N2. For an inorganic compound, however, the products often depend on the decomposition temperature.
Thermogravimetry
One method for determining the products of a thermal decomposition is to monitor the sample’s mass as a function of temperature, a process called thermogravimetry. Figure \(\PageIndex{1}\) shows a typical thermogram in which each change in mass—each “step” in the thermogram—represents the loss of a volatile product. As the following example illustrates, we can use a thermogram to identify a compound’s decomposition reactions.
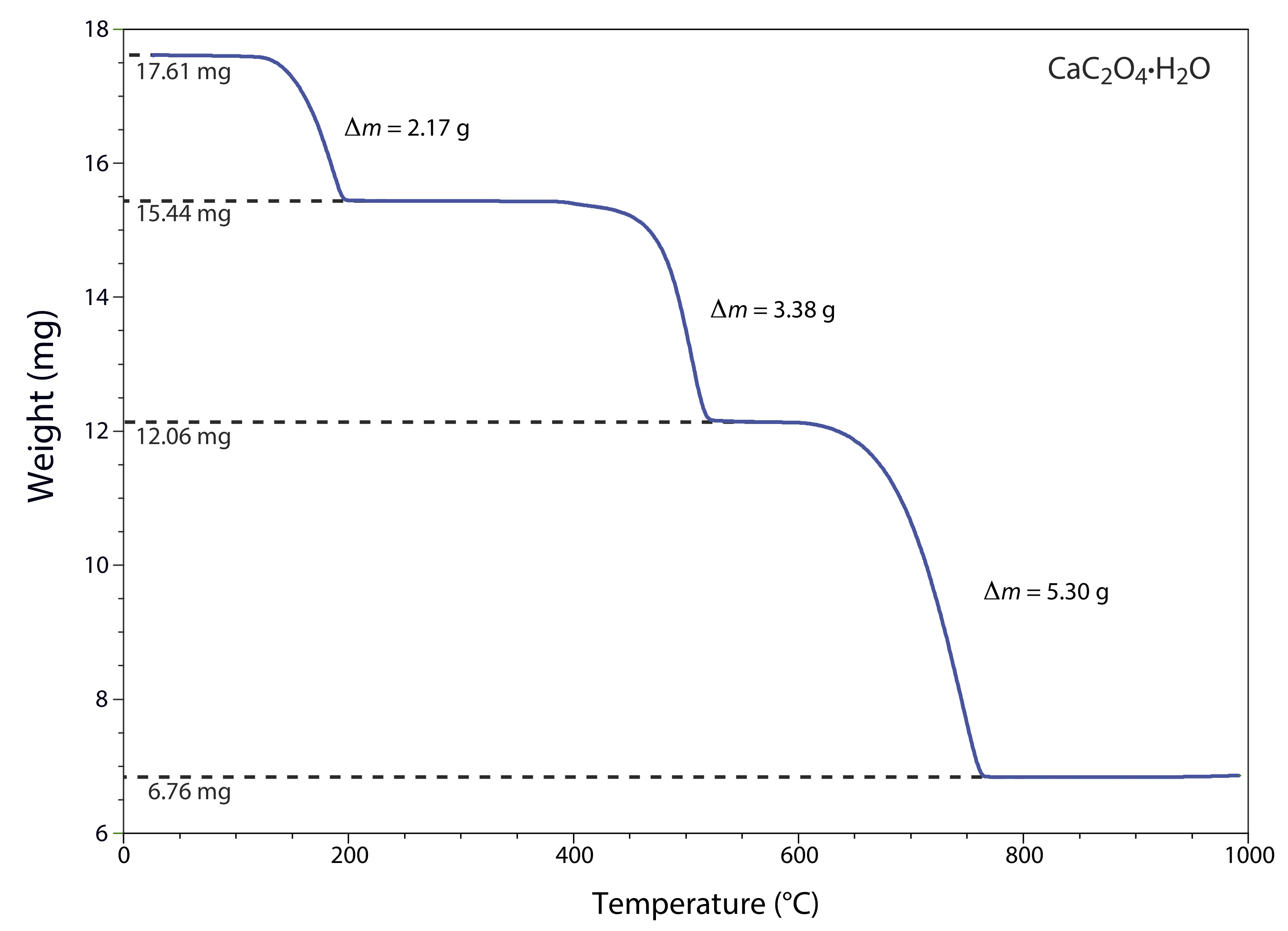
The thermogram in Figure \(\PageIndex{1}\) shows the mass of a sample of calcium oxalate monohydrate, CaC2O4•H2O, as a function of temperature. The original sample of 17.61 mg was heated from room temperature to 1000oC at a rate of 20oC per minute. For each step in the thermogram, identify the volatilization product and the solid residue that remains.
Solution
From 100–250oC the sample loses 17.61 mg – 15.44 mg, or 2.17 mg, which is
\[\frac{2.17 \ \mathrm{mg}}{17.61 \ \mathrm{mg}} \times 100=12.3 \% \nonumber\]
of the sample’s original mass. In terms of CaC2O4•H2O, this corresponds to a decrease in the molar mass of
\[0.123 \times 146.11 \ \mathrm{g} / \mathrm{mol}=18.0 \ \mathrm{g} / \mathrm{mol} \nonumber\]
The product’s molar mass and the temperature range for the decomposition, suggest that this is a loss of H2O(g), leaving a residue of CaC2O4.
The loss of 3.38 mg from 350–550oC is a 19.2% decrease in the sample’s original mass, or a decrease in the molar mass of
\[0.192 \times 146.11 \ \mathrm{g} / \mathrm{mol}=28.1 \ \mathrm{g} / \mathrm{mol} \nonumber\]
which is consistent with the loss of CO(g) and a residue of CaCO3.
Finally, the loss of 5.30 mg from 600-800oC is a 30.1% decrease in the sample’s original mass, or a decrease in molar mass of
\[0.301 \times 146.11 \ \mathrm{g} / \mathrm{mol}=44.0 \ \mathrm{g} / \mathrm{mol} \nonumber\]
This loss in molar mass is consistent with the release of CO2(g), leaving a final residue of CaO. The three decomposition reactions are
\[\begin{array}{c}{\mathrm{CaC}_{2} \mathrm{O}_{4} \cdot \mathrm{H}_{2} \mathrm{O}(s) \rightarrow \ \mathrm{CaC}_{2} \mathrm{O}_{4}(s)+2 \mathrm{H}_{2} \mathrm{O}(l)} \\ {\mathrm{CaC}_{2} \mathrm{O}_{4}(s) \rightarrow \ \mathrm{CaCO}_{3}(s)+\mathrm{CO}(g)} \\ {\mathrm{CaCO}_{3}(s) \rightarrow \ \mathrm{CaO}(s)+\mathrm{CO}_{2}(g)}\end{array} \nonumber\]
Identifying the products of a thermal decomposition provides information that we can use to develop an analytical procedure. For example, the thermogram in Figure \(\PageIndex{1}\) shows that we must heat a precipitate of CaC2O4•H2O to a temperature between 250 and 400oC if we wish to isolate and weigh CaC2O4. Alternatively, heating the sample to 1000oC allows us to isolate and weigh CaO.
Under the same conditions as Figure \(\PageIndex{1}\), the thermogram for a 22.16 mg sample of MgC2O4•H2O shows two steps: a loss of 3.06 mg from 100–250oC and a loss of 12.24 mg from 350–550oC. For each step, identify the volatilization product and the solid residue that remains. Using your results from this exercise and the results from Example \(\PageIndex{1}\), explain how you can use thermogravimetry to analyze a mixture that contains CaC2O4•H2O and MgC2O4•H2O. You may assume that other components in the sample are inert and thermally stable below 1000oC.
- Answer
-
From 100–250oC the sample loses 13.8% of its mass, or a loss of
\[0.138 \times 130.34 \ \mathrm{g} / \mathrm{mol}=18.0 \ \mathrm{g} / \mathrm{mol} \nonumber\]
which is consistent with the loss of H2O(g) and a residue of MgC2O4.
From 350–550oC the sample loses 55.23% of its original mass, or a loss of
\[0.5523 \times 130.34 \ \mathrm{g} / \mathrm{mol}=71.99 \ \mathrm{g} / \mathrm{mol} \nonumber\]
This weight loss is consistent with the simultaneous loss of CO(g) and CO2(g), leaving a residue of MgO.
We can analyze the mixture by heating a portion of the sample to 300oC, 600oC, and 1000oC, recording the mass at each temperature. The loss of mass between 600oC and 1000oC, \(\Delta m_2\), is due to the loss of CO2(g) from the decomposition of CaCO3 to CaO, and is proportional to the mass of CaC2O4•H2O in the sample.
\[\mathrm{g} \ \mathrm{CaC}_{2} \mathrm{O}_{4} \cdot \mathrm{H}_{2} \mathrm{O}=\Delta m_{2} \times \frac{1 \ \mathrm{mol} \ \mathrm{CO}_{2}}{44.01 \ \mathrm{g} \ \mathrm{CO}_{2}} \times \frac{146.11 \ \mathrm{g} \ \mathrm{CaC}_{2} \mathrm{O}_{4} \cdot \mathrm{H}_{2} \mathrm{O}}{\mathrm{mol} \ \mathrm{CO}_{2}} \nonumber\]
The change in mass between 300oC and 600oC, \(\Delta m_1\), is due to the loss of CO(g) from CaC2O4•H2O and the loss of CO(g) and CO2(g) from MgC2O4•H2O. Because we already know the amount of CaC2O4•H2O in the sample, we can calculate its contribution to \(\Delta m_1\).
\[\left(\Delta m_{1}\right)_{\mathrm{Ca}}=\mathrm{g} \ \mathrm{CaC}_{2} \mathrm{O}_{4} \cdot \mathrm{H}_{2} \mathrm{O}=\Delta m_{2} \times \frac{1 \ \mathrm{mol} \ \mathrm{CO}}{146.11 \ \mathrm{g} \ \mathrm{CaC}_{2} \mathrm{O}_{4} \cdot \mathrm{H}_{2} \mathrm{O}} \times \frac{28.01 \ \mathrm{g} \ \mathrm{CO}}{\mathrm{mol} \ \mathrm{CO}} \nonumber\]
The change in mass between 300oC and 600oC due to the decomposition of MgC2O4•H2O
\[\left(m_{1}\right)_{\mathrm{Mg}}=\Delta m_{1}-\left(\Delta m_{1}\right)_{\mathrm{Ca}} \nonumber\]
provides the mass of MgC2O4•H2O in the sample.
\[\mathrm{g} \ \mathrm{MgC}_{2} \mathrm{O}_{4} \cdot \mathrm{H}_{2} \mathrm{O}=\left(\Delta m_{1}\right)_{\mathrm{Mg}} \times \frac{1 \ \mathrm{mol}\left(\mathrm{CO} \ + \ \mathrm{CO}_{2}\right)}{130.35 \ \mathrm{g} \ \mathrm{MgC}_{2} \mathrm{O}_{4} \cdot \mathrm{H}_{2} \mathrm{O}} \times \frac{78.02 \ \mathrm{g} \ \left(\mathrm{CO} \ + \ \mathrm{CO}_{2}\right)}{\mathrm{mol}\ \left(\mathrm{CO} \ + \ \mathrm{CO}_{2}\right)} \nonumber\]
Equipment
Depending on the method of analysis, the equipment for volatilization gravimetry may be simple or complex. In the simplest experimental design, we place the sample in a crucible and decompose it at a fixed temperature using a Bunsen burner, a Meker burner, a laboratory oven, or a muffle furnace. The sample’s mass and the mass of the residue are measured using an analytical balance.
Trapping and weighing the volatile products of a thermal decomposition requires specialized equipment. The sample is placed in a closed container and heated. As decomposition occurs, a stream of an inert purge-gas sweeps the volatile products through one or more selective absorbent traps.
In a thermogravimetric analysis, the sample is placed on a small balance pan attached to one arm of an electromagnetic balance (Figure \(\PageIndex{2}\)). The sample is lowered into an electric furnace and the furnace’s temperature is increased at a fixed rate of few degrees per minute while monitoring continuously the sample’s weight. The instrument usually includes a gas line for purging the volatile decomposition products out of the furnace, and a heat exchanger to dissipate the heat emitted by the furnace.
 |
 |
Figure \(\PageIndex{2}\). (a) Instrumentation for conducting a thermogravimetric analysis. The balance sits on the top of the instrument with the sample suspended below. A gas line supplies an inert gas that sweeps the volatile decomposition products out of the furnace. The heat exchanger dissipates the heat from the furnace to a reservoir of water. (b) Close-up showing the balance pan, which sits on a moving platform, the thermocouple for monitoring temperature, a hook for lowering the sample pan into the furnace, and the opening to the furnace. After placing a small portion of the sample on the balance pan, the platform rotates over the furnace and transfers the balance pan to a hook that is suspended from the balance. Once the balance pan is in place, the platform rotates back to its initial position. The balance pan and the thermocouple are then lowered into the furnace.
Representative Method 8.3.1: Determination of Si in Ores and Alloys
The best way to appreciate the theoretical and practical details discussed in this section is to carefully examine a typical volatilization gravimetric method. Although each method is unique, the determination of Si in ores and alloys by forming volatile SiF4 provides an instructive example of a typical procedure. The description here is based on a procedure from Young, R. S. Chemical Analysis in Extractive Metallurgy, Griffen: London, 1971, pp. 302–304.
Description of Method
Silicon is determined by dissolving the sample in acid and dehydrating to precipitate SiO2. Because a variety of other insoluble oxides also form, the precipitate’s mass is not a direct measure of the amount of silicon in the sample. Treating the solid residue with HF forms volatile SiF4. The decrease in mass following the loss of SiF4 provides an indirect measure of the amount of silicon in the original sample.
Procedure
Transfer a sample of between 0.5 g and 5.0 g to a platinum crucible along with an excess of Na2CO3, and heat until a melt forms. After cooling, dissolve the residue in dilute HCl. Evaporate the solution to dryness on a steam bath and heat the residue, which contains SiO2 and other solids, for one hour at 110oC. Moisten the residue with HCl and repeat the dehydration. Remove any acid soluble materials from the residue by adding 50 mL of water and 5 mL of concentrated HCl. Bring the solution to a boil and filter through #40 filter paper (note: #40 filter paper is a medium speed, ashless filter paper for filtering crystalline solids). Wash the residue with hot 2% v/v HCl followed by hot water. Evaporate the filtrate to dryness twice and, following the same procedure, treat to remove any acid-soluble materials. Combine the two precipitates and dry and ignite to a constant weight at 1200oC. After cooling, add 2 drops of 50% v/v H2SO4 and 10 mL of HF. Remove the volatile SiF4 by evaporating to dryness on a hot plate. Finally, bring the residue to constant weight by igniting at 1200oC.
Questions
1. According to the procedure the sample should weigh between 0.5 g and 5.0 g. How should you decide upon the amount of sample to use?
In this procedure the critical measurement is the decrease in mass following the volatilization of SiF4. The reaction responsible for the loss of mass is
\[\mathrm{SiO}_{2}(s)+4 \mathrm{HF}(a q) \rightarrow \mathrm{SiF}_{4}(g)+2 \mathrm{H}_{2} \mathrm{O}(l ) \nonumber\]
Water and excess HF are removed during the final ignition, and do not contribute to the change in mass. The loss in mass, therefore, is equivalent to the mass of SiO2 present after the dehydration step. Every 0.1 g of Si in the original sample results in the loss of 0.21 g of SiO2. How much sample we use depends on what is an acceptable uncertainty when we measure its mass. A 0.5-g sample that is 50% w/w in Si, for example, will lose 0.53 g. If we are using a balance that measures mass to the nearest ±0.1 mg, then the relative uncertainty in mass is approximately ±0.02%; this is a reasonable level of uncertainty for a gravimetric analysis. A 0.5-g sample that is only 5% w/w Si experiences a weight loss of only 0.053 g and has a relative uncertainty of ±0.2%. In this case a larger sample is needed.
2. Why are acid-soluble materials removed before we treat the dehydrated residue with HF?
Any acid-soluble materials in the sample will react with HF or H2SO4. If the products of these reactions are volatile, or if they decompose at 1200oC, then the change in mass is not due solely to the volatilization of SiF4. As a result, we will overestimate the amount of Si in our sample.
3. Why is H2SO4 added with the HF?
Many samples that contain silicon also contain aluminum and iron, which form Al2O3 and Fe2O3 when we dehydrate the sample. These oxides are potential interferents because they also form volatile fluorides. In the presence of H2SO4, however, aluminum and iron preferentially form non-volatile sulfates, which eventually decompose back to their respective oxides when we heat the residue to 1200oC. As a result, the change in weight after treating with HF and H2SO4 is due only to the loss of SiF4.
Quantitative Applications
Unlike precipitation gravimetry, which rarely is used as a standard method of analysis, volatilization gravimetric methods continue to play an important role in chemical analysis. Several important examples are discussed below.
Inorganic Analysis
Determining the inorganic ash content of an organic material, such as a polymer, is an example of a direct volatilization gravimetric analysis. After weighing the sample, it is placed in an appropriate crucible and the organic material carefully removed by combustion, leaving behind the inorganic ash. The crucible that contains the residue is heated to a constant weight using either a burner or an oven before the mass of the inorganic ash is determined.
Another example of volatilization gravimetry is the determination of dissolved solids in natural waters and wastewaters. In this method, a sample of water is transferred to a weighing dish and dried to a constant weight at either 103–105oC or at 180oC. Samples dried at the lower temperature retain some occluded water and lose some carbonate as CO2; the loss of organic material, however, is minimal at this temperature. At the higher temperature, the residue is free from occluded water, but the loss of carbonate is greater. In addition, some chloride, nitrate, and organic material is lost through thermal decomposition. In either case, the residue that remains after drying to a constant weight at 500oC is the amount of fixed solids in the sample, and the loss in mass provides an indirect measure of the sample’s volatile solids.
Indirect analyses based on the weight of a residue that remains after volatilization are used to determine moisture in a variety of products and to determine silica in waters, wastewaters, and rocks. Moisture is determined by drying a preweighed sample with an infrared lamp or a low temperature oven. The difference between the original weight and the weight after drying equals the mass of water lost.
Organic Analysis
The most important application of volatilization gravimetry is for the elemental analysis of organic materials. During combustion with pure O2, many elements, such as carbon and hydrogen, are released as gaseous combustion products, such as CO2(g) and H2O(g). Passing the combustion products through preweighed tubes that contain selective absorbents and measuring the increase in each tube’s mass provides a direct analysis for the mass of carbon and hydrogen in the sample.
Instead of measuring mass, modern instruments for completing an elemental analysis use gas chromatography (Chapter 12) or infrared spectroscopy (Chapter 10) to monitor the gaseous decomposition products.
Alkaline metals and earths in organic materials are determined by adding H2SO4 to the sample before combustion. After combustion is complete, the metal remains behind as a solid residue of metal sulfate. Silver, gold, and platinum are determined by burning the organic sample, leaving a metallic residue of Ag, Au, or Pt. Other metals are determined by adding HNO3 before combustion, which leaves a residue of the metal oxide.
Volatilization gravimetry also is used to determine biomass in waters and wastewaters. Biomass is a water quality index that provides an indication of the total mass of organisms contained within a sample of water. A known volume of the sample is passed through a preweighed 0.45-μm membrane filter or a glass-fiber filter and dried at 105oC for 24 h. The residue’s mass provides a direct measure of biomass. If samples are known to contain a substantial amount of dissolved inorganic solids, the residue is ignited at 500oC for one hour, which volatilizes the biomass. The resulting inorganic residue is wetted with distilled water to rehydrate any clay minerals and dried to a constant weight at 105oC. The difference in mass before and after ignition provides an indirect measure of biomass.
Quantitative Calculations
For some applications, such as determining the amount of inorganic ash in a polymer, a quantitative calculation is straightforward and does not require a balanced chemical reaction. For other applications, however, the relationship between the analyte and the analytical signal depends upon the stoichiometry of any relevant reactions. Once again, a conservation of mass is useful when solving problems.
A 101.3-mg sample of an organic compound that contains chlorine is combusted in pure O2. The volatile gases are collected in absorbent traps with the trap for CO2 increasing in mass by 167.6 mg and the trap for H2O increasing in mass by 13.7-mg. A second sample of 121.8 mg is treated with concentrated HNO3, producing Cl2 that reacts with Ag+ to form 262.7 mg of AgCl. Determine the compound’s composition, as well as its empirical formula.
Solution
A conservation of mass requires that all the carbon in the organic compound is in the CO2 produced during combustion; thus
\[0.1676 \ \mathrm{g} \ \mathrm{CO}_{2} \times \frac{1 \ \mathrm{mol} \ \mathrm{C}}{44.010 \ \mathrm{g} \ \mathrm{CO}_{2}} \times \frac{12.011 \ \mathrm{g} \ \mathrm{C}}{\mathrm{mol} \ \mathrm{C}}=0.04574 \ \text{g C} \nonumber\]
\[\frac{0.04574 \ \mathrm{g} \ \mathrm{C}}{0.1013 \ \mathrm{g} \text { sample }} \times 100=45.15 \% \mathrm{w} / \mathrm{w} \ \mathrm{C} \nonumber\]
Using the same approach for hydrogen and chlorine, we find that
\[0.0137 \ \mathrm{g} \ \mathrm{H}_{2} \mathrm{O} \times \frac{2 \ \mathrm{mol} \ \mathrm{H}}{18.015 \ \mathrm{g} \ \mathrm{H}_{2} \mathrm{O}} \times \frac{1.008 \ \mathrm{g} \ \mathrm{H}}{\mathrm{mol} \ \mathrm{H}}=1.533 \times 10^{-3} \mathrm{g} \ \mathrm{H} \nonumber\]
\[\frac{1.533 \ \times 10^{-3} \mathrm{g} \ \mathrm{H}}{0.1003 \ \mathrm{g} \ \text { sample }} \times 100=1.53 \% \mathrm{w} / \mathrm{w} \ \mathrm{H} \nonumber\]
\[0.2627 \ \mathrm{g} \ \mathrm{AgCl} \times \frac{1 \ \mathrm{mol} \ \mathrm{Cl}}{143.32 \ \mathrm{g} \ \mathrm{AgCl}} \times \frac{35.455 \ \text{g Cl}}{\mathrm{mol} \ \mathrm{Cl}}=0.06498 \ \mathrm{g} \ \mathrm{Cl} \nonumber\]
\[\frac{0.06498 \ \mathrm{g} \ \mathrm{Cl}}{0.1218 \ \mathrm{g} \text { sample }} \times 100=53.35 \% \mathrm{w} / \mathrm{w} \ \mathrm{Cl} \nonumber\]
Adding together the weight percents for C, H, and Cl gives a total of 100.03%; thus, the compound contains only these three elements. To determine the compound’s empirical formula we note that a gram of sample contains 0.4515 g of C, 0.0153 g of H and 0.5335 g of Cl. Expressing each element in moles gives 0.0376 moles C, 0.0152 moles H and 0.0150 moles Cl. Hydrogen and chlorine are present in a 1:1 molar ratio. The molar ratio of C to moles of H or Cl is
\[\frac{\mathrm{mol} \ \mathrm{C}}{\mathrm{mol} \text{ H}} =\frac{\mathrm{mol} \ \mathrm{C}}{\mathrm{mol} \ \mathrm{Cl}}=\frac{0.0376}{0.0150}=2.51 \approx 2.5 \nonumber\]
Thus, the simplest, or empirical formula for the compound is C5H2Cl2.
In an indirect volatilization gravimetric analysis, the change in the sample’s weight is proportional to the amount of analyte in the sample. Note that in the following example it is not necessary to apply a conservation of mass to relate the analytical signal to the analyte.
A sample of slag from a blast furnace is analyzed for SiO2 by decomposing a 0.5003-g sample with HCl, leaving a residue with a mass of 0.1414 g. After treating with HF and H2SO4, and evaporating the volatile SiF4, a residue with a mass of 0.0183 g remains. Determine the %w/w SiO2 in the sample.
Solution
The difference in the residue’s mass before and after volatilizing SiF4 gives the mass of SiO2 in the sample; thus the sample contains
\[0.1414 \ \mathrm{g}-0.0183 \ \mathrm{g}=0.1231 \ \mathrm{g} \ \mathrm{SiO}_{2} \nonumber\]
and the %w/w SiO2 is
\[\frac{0.1231 \ \mathrm{g} \ \mathrm{Si} \mathrm{O}_{2}}{0.5003 \ \mathrm{g} \text { sample }} \times 100=24.61 \% \mathrm{w} / \mathrm{w} \ \mathrm{SiO}_{2} \nonumber\]
Heating a 0.3317-g mixture of CaC2O4 and MgC2O4 yields a residue of 0.1794 g at 600oC and a residue of 0.1294 g at 1000oC. Calculate the %w/w CaC2O4 in the sample. You may wish to review your answer to Exercise \(\PageIndex{1}\) as you consider this problem.
- Answer
-
In Exercise \(\PageIndex{1}\) we developed an equation for the mass of CaC2O4•H2O in a mixture of CaC2O4•H2O, MgC2O4•H2O, and inert materials. Adapting this equation to a sample that contains CaC2O4, MgC2O4, and inert materials is easy; thus
\[\mathrm{g} \ \mathrm{CaC}_{2} \mathrm{O}_{4}=(0.1794 \ \mathrm{g}-0.1294 \ \mathrm{g}) \times \frac{1 \ \mathrm{mol} \ \mathrm{CO}_{2}}{44.01 \ \mathrm{g} \ \mathrm{CO}_{2}} \times \frac{128.10 \ \mathrm{g} \ \mathrm{CaC}_{2} \mathrm{O}_{4}}{\mathrm{mol} \ \mathrm{CO}_{2}}=0.1455 \ \mathrm{g} \ \mathrm{CaC}_{2} \mathrm{O}_{4} \nonumber\]
The %w/w CaC2O4 in the sample is
\[\frac{0.1455 \ \mathrm{g} \ \mathrm{CaC}_{2} \mathrm{O}_{4}}{0.3317 \ \mathrm{g} \text { sample }} \times 100=43.86 \% \mathrm{w} / \mathrm{w} \mathrm{CaC}_{2} \mathrm{O}_{4} \nonumber\]
Finally, for some quantitative applications we can compare the result for a sample to a similar result obtained using a standard.
A 26.23-mg sample of MgC2O4•H2O and inert materials is heated to constant weight at 1200oC, leaving a residue that weighs 20.98 mg. A sample of pure MgC2O4•H2O, when treated in the same fashion, undergoes a 69.08% change in its mass. Determine the %w/w MgC2O4•H2O in the sample.
Solution
The change in the sample’s mass is 5.25 mg, which corresponds to
\[5.25 \ \mathrm{mg} \operatorname{lost} \times \frac{100.0 \ \mathrm{mg} \ \mathrm{MgC}_{2} \mathrm{O}_{4} \cdot \mathrm{H}_{2} \mathrm{O}}{69.08 \ \mathrm{mg} \text { lost }}=7.60 \ \mathrm{mg} \ \mathrm{MgC}_{2} \mathrm{O}_{4} \cdot \mathrm{H}_{2} \mathrm{O} \nonumber\]
The %w/w MgC2O4•H2O in the sample is
\[\frac{7.60 \ \mathrm{mg} \ \mathrm{MgC}_{2} \mathrm{O}_{4} \cdot \mathrm{H}_{2} \mathrm{O}}{26.23 \ \mathrm{mg} \text { sample }} \times 100=29.0 \% \mathrm{w} / \mathrm{w} \ \mathrm{MgC}_{2} \mathrm{O}_{4} \cdot \mathrm{H}_{2} \mathrm{O} \nonumber\]
Evaluating Volatilization Gravimetry
The scale of operation, accuracy, and precision of a gravimetric volatilization method is similar to that described in the last section for precipitation gravimetry. The sensitivity of a direct analysis is fixed by the analyte’s chemical form following combustion or volatilization. We can improve the sensitivity of an indirect analysis by choosing conditions that give the largest possible change in mass. For example, the thermogram in Figure \(\PageIndex{1}\) shows us that an indirect analysis for CaC2O4•H2O is more sensitive if we measure the change in mass following ignition at 1000oC than if we ignite the sample at 300oC.
Selectivity is not a problem for a direct analysis if we trap the analyte using a selective absorbent trap. A direct analysis based on the residue’s weight following combustion or volatilization is possible if the residue contains only the analyte of interest. As noted earlier, an indirect analysis only is feasible when the change in mass results from the loss of a single volatile product that contains the analyte.
Volatilization gravimetric methods are time and labor intensive. Equipment needs are few, except when combustion gases must be trapped, or for a thermogravimetric analysis, when specialized instrumentation is needed.


