8.3: Stoichiometry of Gaseous Substances, Mixtures, and Reactions
- Page ID
- 221184
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)↵
- Use the ideal gas law to compute gas densities and molar masses
- Perform stoichiometric calculations involving gaseous substances
- State Dalton’s law of partial pressures and use it in calculations involving gaseous mixtures
The study of the chemical behavior of gases was part of the basis of perhaps the most fundamental chemical revolution in history. French nobleman Antoine Lavoisier, widely regarded as the “father of modern chemistry,” changed chemistry from a qualitative to a quantitative science through his work with gases. He discovered the law of conservation of matter, discovered the role of oxygen in combustion reactions, determined the composition of air, explained respiration in terms of chemical reactions, and more. He was a casualty of the French Revolution, guillotined in 1794. Of his death, mathematician and astronomer Joseph-Louis Lagrange said, “It took the mob only a moment to remove his head; a century will not suffice to reproduce it."
As described in an earlier chapter of this text, we can turn to chemical stoichiometry for answers to many of the questions that ask “How much?” We can answer the question with masses of substances or volumes of solutions. However, we can also answer this question another way: with volumes of gases. We can use the ideal gas equation to relate the pressure, volume, temperature, and number of moles of a gas. Here we will combine the ideal gas equation with other equations to find gas density and molar mass. We will deal with mixtures of different gases, and calculate amounts of substances in reactions involving gases. This section will not introduce any new material or ideas, but will provide examples of applications and ways to integrate concepts we have already discussed.
Density of a Gas
Recall that the density of a gas is its mass to volume ratio, \(ρ=\dfrac{m}{V}\). Therefore, if we can determine the mass of some volume of a gas, we will get its density. The density of an unknown gas can used to determine its molar mass and thereby assist in its identification. The ideal gas law, PV = nRT, provides us with a means of deriving such a mathematical formula to relate the density of a gas to its volume in the proof shown in Example \(\PageIndex{1}\).
Use PV = nRT to derive a formula for the density of gas in g/L
Solution
\[PV = nRT \nonumber \]
Rearrange to get (mol/L):
\[\dfrac{n}{v}=\dfrac{P}{RT} \nonumber \]
Multiply each side of the equation by the molar mass, ℳ. When moles are multiplied by ℳ in g/mol, g are obtained:
\[(ℳ)\left(\dfrac{n}{V}\right)=\left(\dfrac{P}{RT}\right)(ℳ) \nonumber \]
\[ℳ/V=ρ=\dfrac{Pℳ}{RT} \nonumber \]
A gas was found to have a density of 0.0847 g/L at 17.0 °C and a pressure of 760 torr. What is its molar mass? What is the gas?
- Answer
-
\[ρ=\dfrac{Pℳ}{RT} \nonumber \]
\[\mathrm{0.0847\:g/L=760\cancel{torr}×\dfrac{1\cancel{atm}}{760\cancel{torr}}×\dfrac{\mathit{ℳ}}{0.0821\: L\cancel{atm}/mol\: K}×290\: K} \nonumber \]
ℳ = 2.02 g/mol; therefore, the gas must be hydrogen (H2, 2.02 g/mol)
We must specify both the temperature and the pressure of a gas when calculating its density because the number of moles of a gas (and thus the mass of the gas) in a liter changes with temperature or pressure. Gas densities are often reported at STP.
Using the Ideal Gas Law and Density of a Gas Cyclopropane, a gas once used with oxygen as a general anesthetic, is composed of 85.7% carbon and 14.3% hydrogen by mass. Find the empirical formula. If 1.56 g of cyclopropane occupies a volume of 1.00 L at 0.984 atm and 50 °C, what is the molecular formula for cyclopropane?
Solution
Strategy:
First solve the empirical formula problem using methods discussed earlier. Assume 100 g and convert the percentage of each element into grams. Determine the number of moles of carbon and hydrogen in the 100-g sample of cyclopropane. Divide by the smallest number of moles to relate the number of moles of carbon to the number of moles of hydrogen. In the last step, realize that the smallest whole number ratio is the empirical formula:
\[\mathrm{85.7\: g\: C×\dfrac{1\: mol\: C}{12.01\: g\: C}=7.136\: mol\: C\hspace{20px}\dfrac{7.136}{7.136}=1.00\: mol\: C} \nonumber \]
\[\mathrm{14.3\: g\: H×\dfrac{1\: mol\: H}{1.01\: g\: H}=14.158\: mol\: H\hspace{20px}\dfrac{14.158}{7.136}=1.98\: mol\: H} \nonumber \]
Empirical formula is CH2 [empirical mass (EM) of 14.03 g/empirical unit].
Next, use the density equation related to the ideal gas law to determine the molar mass:
\[d=\dfrac{Pℳ}{RT}\hspace{20px}\mathrm{\dfrac{1.56\: g}{1.00\: L}=0.984\: atm×\dfrac{ℳ}{0.0821\: L\: atm/mol\: K}×323\: K} \nonumber \]
ℳ = 42.0 g/mol, \(\dfrac{ℳ}{Eℳ}=\dfrac{42.0}{14.03}=2.99\), so (3)(CH2) = C3H6 (molecular formula)
Acetylene, a fuel used welding torches, is comprised of 92.3% C and 7.7% H by mass. Find the empirical formula. If 1.10 g of acetylene occupies of volume of 1.00 L at 1.15 atm and 59.5 °C, what is the molecular formula for acetylene?
- Answer
-
Empirical formula, CH; Molecular formula, C2H2
Molar Mass of a Gas
Another useful application of the ideal gas law involves the determination of molar mass. By definition, the molar mass of a substance is the ratio of its mass in grams, m, to its amount in moles, n:
\[ℳ=\mathrm{\dfrac{grams\: of\: substance}{moles\: of\: substance}}=\dfrac{m}{n} \nonumber \]
The ideal gas equation can be rearranged to isolate n:
\[n=\dfrac{PV}{RT} \nonumber \]
and then combined with the molar mass equation to yield:
\[ℳ=\dfrac{mRT}{PV} \nonumber \]
This equation can be used to derive the molar mass of a gas from measurements of its pressure, volume, temperature, and mass.
The approximate molar mass of a volatile liquid can be determined by:
- Heating a sample of the liquid in a flask with a tiny hole at the top, which converts the liquid into gas that may escape through the hole
- Removing the flask from heat at the instant when the last bit of liquid becomes gas, at which time the flask will be filled with only gaseous sample at ambient pressure
- Sealing the flask and permitting the gaseous sample to condense to liquid, and then weighing the flask to determine the sample’s mass (Figure \(\PageIndex{1}\))

Using this procedure, a sample of chloroform gas weighing 0.494 g is collected in a flask with a volume of 129 cm3 at 99.6 °C when the atmospheric pressure is 742.1 mm Hg. What is the approximate molar mass of chloroform?
Solution
Since
\[ℳ=\dfrac{m}{n} \nonumber \]
and
\[n=\dfrac{PV}{RT} \nonumber \]
substituting and rearranging gives
\[ℳ=\dfrac{mRT }{PV} \nonumber \]
then
\[ℳ=\dfrac{mRT}{PV}=\mathrm{\dfrac{(0.494\: g)×0.08206\: L⋅atm/mol\: K×372.8\: K}{0.976\: atm×0.129\: L}=120\:g/mol} \nonumber \]
A sample of phosphorus that weighs 3.243 × 10−2 g exerts a pressure of 31.89 kPa in a 56.0-mL bulb at 550 °C. What are the molar mass and molecular formula of phosphorus vapor?
- Answer
-
124 g/mol P4
The Pressure of a Mixture of Gases: Dalton’s Law
Unless they chemically react with each other, the individual gases in a mixture of gases do not affect each other’s pressure. Each individual gas in a mixture exerts the same pressure that it would exert if it were present alone in the container ( Figure \(\PageIndex{2}\)). The pressure exerted by each individual gas in a mixture is called its partial pressure. This observation is summarized by Dalton’s law of partial pressures: The total pressure of a mixture of ideal gases is equal to the sum of the partial pressures of the component gases:
\[P_{Total}=P_A+P_B+P_C+...=\sum_iP_i \nonumber \]
In the equation PTotal is the total pressure of a mixture of gases, PA is the partial pressure of gas A; PB is the partial pressure of gas B; PC is the partial pressure of gas C; and so on.
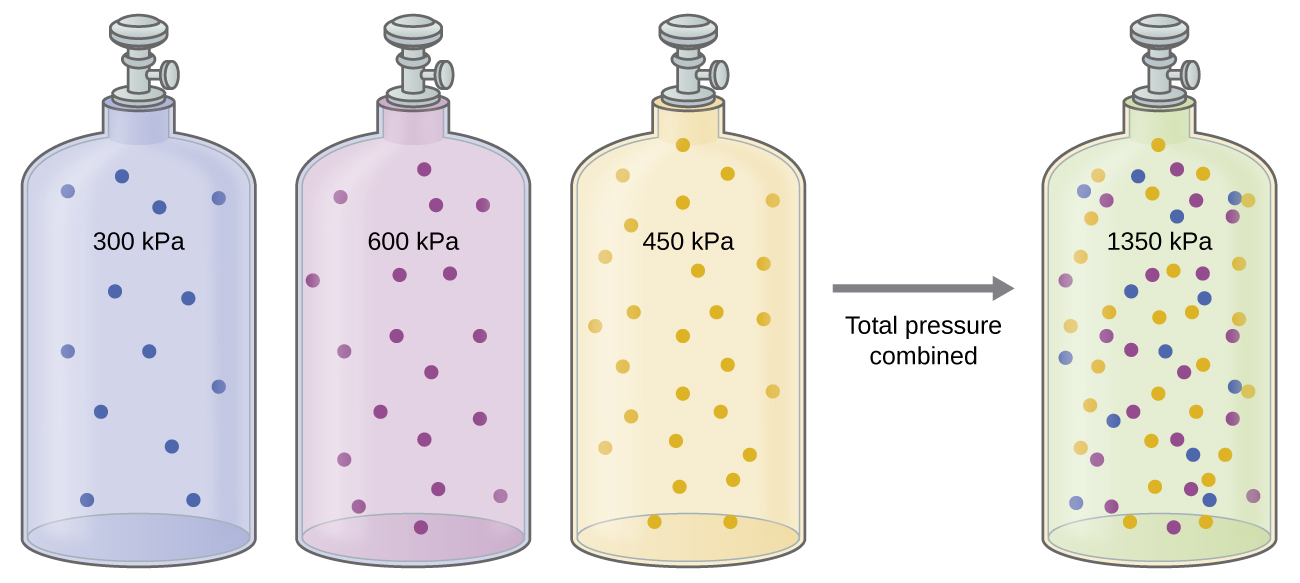
The partial pressure of gas A is related to the total pressure of the gas mixture via its mole fraction (X), a unit of concentration defined as the number of moles of a component of a solution divided by the total number of moles of all components:
\[P_A=X_A×P_{Total}\hspace{20px}\ce{where}\hspace{20px}X_A=\dfrac{n_A}{n_{Total}} \nonumber \]
where PA, XA, and nA are the partial pressure, mole fraction, and number of moles of gas A, respectively, and nTotal is the number of moles of all components in the mixture.
A 10.0-L vessel contains 2.50 × 10−3 mol of H2, 1.00 × 10−3 mol of He, and 3.00 × 10−4 mol of Ne at 35 °C.
- What are the partial pressures of each of the gases?
- What is the total pressure in atmospheres?
Solution
The gases behave independently, so the partial pressure of each gas can be determined from the ideal gas equation, using \(P=\dfrac{nRT}{V}\):
\[P_\mathrm{H_2}=\mathrm{\dfrac{(2.50×10^{−3}\:mol)(0.08206\cancel{L}atm\cancel{mol^{−1}\:K^{−1}})(308\cancel{K})}{10.0\cancel{L}}=6.32×10^{−3}\:atm} \nonumber \]
\[P_\ce{He}=\mathrm{\dfrac{(1.00×10^{−3}\cancel{mol})(0.08206\cancel{L}atm\cancel{mol^{−1}\:K^{−1}})(308\cancel{K})}{10.0\cancel{L}}=2.53×10^{−3}\:atm} \nonumber \]
\[P_\ce{Ne}=\mathrm{\dfrac{(3.00×10^{−4}\cancel{mol})(0.08206\cancel{L}atm\cancel{mol^{−1}\:K^{−1}})(308\cancel{K})}{10.0\cancel{L}}=7.58×10^{−4}\:atm} \nonumber \]
The total pressure is given by the sum of the partial pressures:
\[P_\ce{T}=P_\mathrm{H_2}+P_\ce{He}+P_\ce{Ne}=\mathrm{(0.00632+0.00253+0.00076)\:atm=9.61×10^{−3}\:atm} \nonumber \]
A 5.73-L flask at 25 °C contains 0.0388 mol of N2, 0.147 mol of CO, and 0.0803 mol of H2. What is the total pressure in the flask in atmospheres?
- Answer
-
1.137 atm
Here is another example of this concept, but dealing with mole fraction calculations.
A gas mixture used for anesthesia contains 2.83 mol oxygen, O2, and 8.41 mol nitrous oxide, N2O. The total pressure of the mixture is 192 kPa.
- What are the mole fractions of O2 and N2O?
- What are the partial pressures of O2 and N2O?
Solution
The mole fraction is given by
\[X_A=\dfrac{n_A}{n_{Total}} \nonumber \]
and the partial pressure is
\[P_A = X_A \times P_{Total} \nonumber \]
For O2,
\[X_{O_2}=\dfrac{n_{O_2}}{n_{Total}}=\mathrm{\dfrac{2.83 mol}{(2.83+8.41)\:mol}=0.252} \nonumber \]
and
\[P_{O_2}=X_{O_2}×P_{Total}=\mathrm{0.252×192\: kPa=48.4\: kPa} \nonumber \]
For N2O,
\[X_{N_2O}=\dfrac{n_{N_2O}}{n_{Total}}=\mathrm{\dfrac{8.41\: mol}{(2.83+8.41)\:mol}=0.748} \nonumber \]
and
\[P_{N_2O}=X_{N_2O}×P_{Total}=\mathrm{(0.748)×192\: kPa = 143.6 \: kPa} \nonumber \]
What is the pressure of a mixture of 0.200 g of H2, 1.00 g of N2, and 0.820 g of Ar in a container with a volume of 2.00 L at 20 °C?
- Answer
-
1.87 atm
Collection of Gases over Water
A simple way to collect gases that do not react with water is to capture them in a bottle that has been filled with water and inverted into a dish filled with water. The pressure of the gas inside the bottle can be made equal to the air pressure outside by raising or lowering the bottle. When the water level is the same both inside and outside the bottle (Figure \(\PageIndex{3}\)), the pressure of the gas is equal to the atmospheric pressure, which can be measured with a barometer.
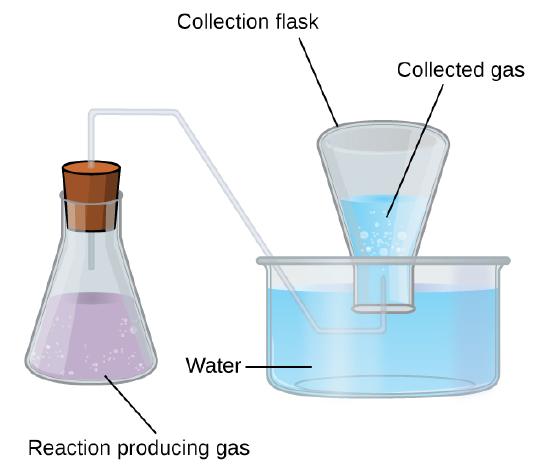
However, there is another factor we must consider when we measure the pressure of the gas by this method. Water evaporates and there is always gaseous water (water vapor) above a sample of liquid water. As a gas is collected over water, it becomes saturated with water vapor and the total pressure of the mixture equals the partial pressure of the gas plus the partial pressure of the water vapor. The pressure of the pure gas is therefore equal to the total pressure minus the pressure of the water vapor—this is referred to as the “dry” gas pressure, that is, the pressure of the gas only, without water vapor.
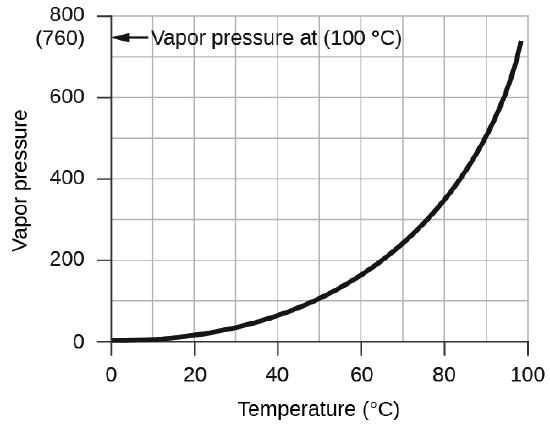
The vapor pressure of water, which is the pressure exerted by water vapor in equilibrium with liquid water in a closed container, depends on the temperature (Figure \(\PageIndex{4}\)); more detailed information on the temperature dependence of water vapor can be found in Table \(\PageIndex{1}\), and vapor pressure will be discussed in more detail in the next chapter on liquids.
| Temperature (°C) | Pressure (torr) | Temperature (°C) | Pressure (torr) | Temperature (°C) | Pressure (torr) | ||
|---|---|---|---|---|---|---|---|
| –10 | 1.95 | 18 | 15.5 | 30 | 31.8 | ||
| –5 | 3.0 | 19 | 16.5 | 35 | 42.2 | ||
| –2 | 3.9 | 20 | 17.5 | 40 | 55.3 | ||
| 0 | 4.6 | 21 | 18.7 | 50 | 92.5 | ||
| 2 | 5.3 | 22 | 19.8 | 60 | 149.4 | ||
| 4 | 6.1 | 23 | 21.1 | 70 | 233.7 | ||
| 6 | 7.0 | 24 | 22.4 | 80 | 355.1 | ||
| 8 | 8.0 | 25 | 23.8 | 90 | 525.8 | ||
| 10 | 9.2 | 26 | 25.2 | 95 | 633.9 | ||
| 12 | 10.5 | 27 | 26.7 | 99 | 733.2 | ||
| 14 | 12.0 | 28 | 28.3 | 100.0 | 760.0 | ||
| 16 | 13.6 | 29 | 30.0 | 101.0 | 787.6 |
If 0.200 L of argon is collected over water at a temperature of 26 °C and a pressure of 750 torr in a system like that shown in Figure \(\PageIndex{3}\), what is the partial pressure of argon?
Solution
According to Dalton’s law, the total pressure in the bottle (750 torr) is the sum of the partial pressure of argon and the partial pressure of gaseous water:
\[P_\ce{T}=P_\ce{Ar}+P_\mathrm{H_2O} \nonumber \]
Rearranging this equation to solve for the pressure of argon gives:
\[P_\ce{Ar}=P_\ce{T}−P_\mathrm{H_2O} \nonumber \]
The pressure of water vapor above a sample of liquid water at 26 °C is 25.2 torr (Appendix E), so:
\[P_\ce{Ar}=\mathrm{750\:torr−25.2\:torr=725\:torr} \nonumber \]
A sample of oxygen collected over water at a temperature of 29.0 °C and a pressure of 764 torr has a volume of 0.560 L. What volume would the dry oxygen have under the same conditions of temperature and pressure?
- Answer
-
0.583 L
Chemical Stoichiometry and Gases
Chemical stoichiometry describes the quantitative relationships between reactants and products in chemical reactions. We have previously measured quantities of reactants and products using masses for solids and volumes in conjunction with the molarity for solutions; now we can also use gas volumes to indicate quantities. If we know the volume, pressure, and temperature of a gas, we can use the ideal gas equation to calculate how many moles of the gas are present. If we know how many moles of a gas are involved, we can calculate the volume of a gas at any temperature and pressure.
Avogadro’s Law Revisited
Sometimes we can take advantage of a simplifying feature of the stoichiometry of gases that solids and solutions do not exhibit: All gases that show ideal behavior contain the same number of molecules in the same volume (at the same temperature and pressure). Thus, the ratios of volumes of gases involved in a chemical reaction are given by the coefficients in the equation for the reaction, provided that the gas volumes are measured at the same temperature and pressure.
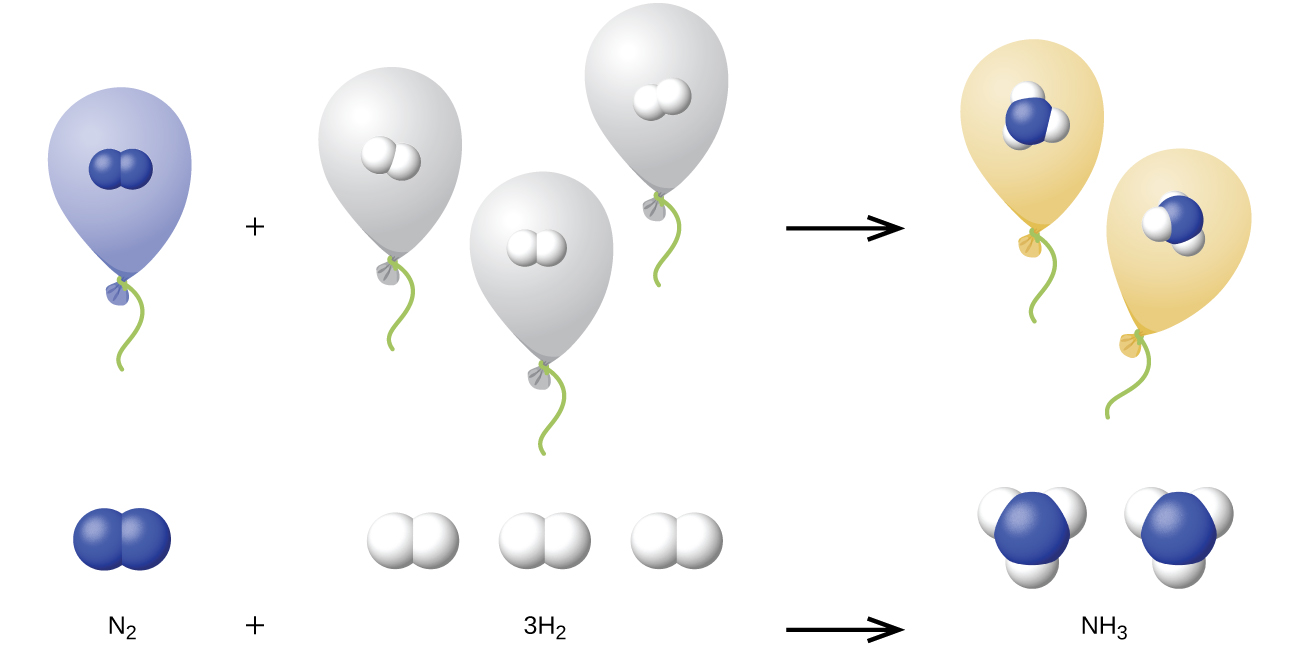
We can extend Avogadro’s law (that the volume of a gas is directly proportional to the number of moles of the gas) to chemical reactions with gases: Gases combine, or react, in definite and simple proportions by volume, provided that all gas volumes are measured at the same temperature and pressure. For example, since nitrogen and hydrogen gases react to produce ammonia gas according to
\[\ce{N2}(g)+\ce{3H2}(g)⟶\ce{2NH3}(g) \nonumber \]
a given volume of nitrogen gas reacts with three times that volume of hydrogen gas to produce two times that volume of ammonia gas, if pressure and temperature remain constant.
The explanation for this is illustrated in Figure \(\PageIndex{4}\). According to Avogadro’s law, equal volumes of gaseous N2, H2, and NH3, at the same temperature and pressure, contain the same number of molecules. Because one molecule of N2 reacts with three molecules of H2 to produce two molecules of NH3, the volume of H2 required is three times the volume of N2, and the volume of NH3 produced is two times the volume of N2.
Propane, C3H8(g), is used in gas grills to provide the heat for cooking. What volume of O2(g) measured at 25 °C and 760 torr is required to react with 2.7 L of propane measured under the same conditions of temperature and pressure? Assume that the propane undergoes complete combustion.
Solution
The ratio of the volumes of C3H8 and O2 will be equal to the ratio of their coefficients in the balanced equation for the reaction:
\[\begin{align}
&\ce{C3H8}(g)+\ce{5O2}(g) ⟶ &&\ce{3CO2}(g)+\ce{4H2O}(l)\\
\ce{&1\: volume + 5\: volumes &&3\: volumes + 4\: volumes}
\end{align} \nonumber \]
From the equation, we see that one volume of C3H8 will react with five volumes of O2:
\[\mathrm{2.7\cancel{L\:C_3H_8}×\dfrac{5\: L\:\ce{O2}}{1\cancel{L\:C_3H_8}}=13.5\: L\:\ce{O2}} \nonumber \]
A volume of 13.5 L of O2 will be required to react with 2.7 L of C3H8.
An acetylene tank for an oxyacetylene welding torch provides 9340 L of acetylene gas, C2H2, at 0 °C and 1 atm. How many tanks of oxygen, each providing 7.00 × 103 L of O2 at 0 °C and 1 atm, will be required to burn the acetylene?
\[\ce{2C2H2 + 5O2⟶4CO2 + 2H2O} \nonumber \]
- Answer
-
3.34 tanks (2.34 × 104 L)
Ammonia is an important fertilizer and industrial chemical. Suppose that a volume of 683 billion cubic feet of gaseous ammonia, measured at 25 °C and 1 atm, was manufactured. What volume of H2(g), measured under the same conditions, was required to prepare this amount of ammonia by reaction with N2?
\[\ce{N2}(g)+\ce{3H2}(g)⟶\ce{2NH3}(g) \nonumber \]
Solution
Because equal volumes of H2 and NH3 contain equal numbers of molecules and each three molecules of H2 that react produce two molecules of NH3, the ratio of the volumes of H2 and NH3 will be equal to 3:2. Two volumes of NH3, in this case in units of billion ft3, will be formed from three volumes of H2:
\[\mathrm{683\cancel{billion\:ft^3\:NH_3}×\dfrac{3\: billion\:ft^3\:H_2}{2\cancel{billion\:ft^3\:NH_3}}=1.02×10^3\:billion\:ft^3\:H_2} \nonumber \]
The manufacture of 683 billion ft3 of NH3 required 1020 billion ft3 of H2. (At 25 °C and 1 atm, this is the volume of a cube with an edge length of approximately 1.9 miles.)
What volume of O2(g) measured at 25 °C and 760 torr is required to react with 17.0 L of ethylene, C2H4(g), measured under the same conditions of temperature and pressure? The products are CO2 and water vapor.
- Answer
-
51.0 L
What volume of hydrogen at 27 °C and 723 torr may be prepared by the reaction of 8.88 g of gallium with an excess of hydrochloric acid?
\[\ce{2Ga}(s)+\ce{6HCl}(aq)⟶\ce{2GaCl3}(aq)+\ce{3H2}(g) \nonumber \]
Solution
To convert from the mass of gallium to the volume of H2(g), we need to do something like this:

The first two conversions are:
\[\mathrm{8.88\cancel{g\: Ga}×\dfrac{1\cancel{mol\: Ga}}{69.723\cancel{g\: Ga}}×\dfrac{3\: mol\:H_2}{2\cancel{mol\: Ga}}=0.191\:mol\: H_2} \nonumber \]
Finally, we can use the ideal gas law:
\[V_\mathrm{H_2}=\left(\dfrac{nRT}{P}\right)_\mathrm{H_2}=\mathrm{\dfrac{0.191\cancel{mol}×0.08206\: L\cancel{atm\:mol^{−1}\:K^{−1}}×300\: K}{0.951\:atm}=4.94\: L} \nonumber \]
Sulfur dioxide is an intermediate in the preparation of sulfuric acid. What volume of SO2 at 343 °C and 1.21 atm is produced by burning l.00 kg of sulfur in oxygen?
- Answer
-
1.30 × 103 L
The thin skin of our atmosphere keeps the earth from being an ice planet and makes it habitable. In fact, this is due to less than 0.5% of the air molecules. Of the energy from the sun that reaches the earth, almost \(\dfrac{1}{3}\) is reflected back into space, with the rest absorbed by the atmosphere and the surface of the earth. Some of the energy that the earth absorbs is re-emitted as infrared (IR) radiation, a portion of which passes back out through the atmosphere into space. However, most of this IR radiation is absorbed by certain substances in the atmosphere, known as greenhouse gases, which re-emit this energy in all directions, trapping some of the heat. This maintains favorable living conditions—without atmosphere, the average global average temperature of 14 °C (57 °F) would be about –19 °C (–2 °F). The major greenhouse gases (GHGs) are water vapor, carbon dioxide, methane, and ozone. Since the Industrial Revolution, human activity has been increasing the concentrations of GHGs, which have changed the energy balance and are significantly altering the earth’s climate (Figure \(\PageIndex{6}\)).
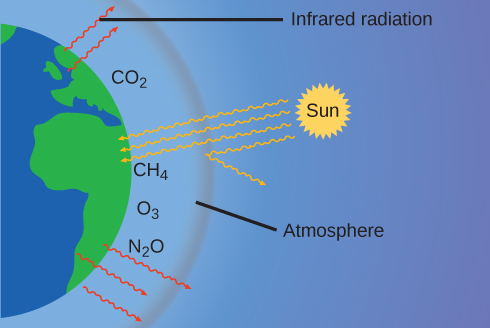
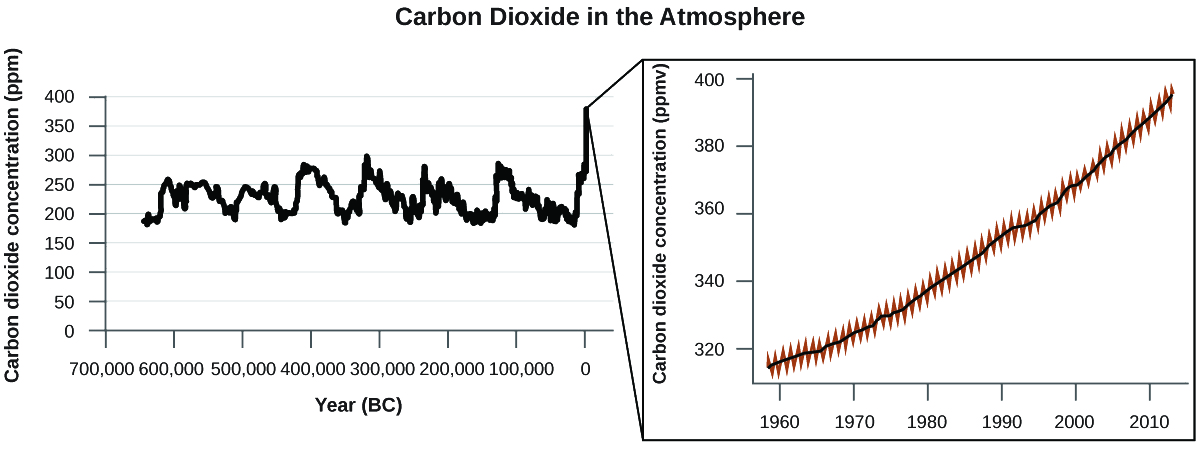
There is strong evidence from multiple sources that higher atmospheric levels of CO2 are caused by human activity, with fossil fuel burning accounting for about \(\dfrac{3}{4}\) of the recent increase in CO2. Reliable data from ice cores reveals that CO2 concentration in the atmosphere is at the highest level in the past 800,000 years; other evidence indicates that it may be at its highest level in 20 million years. In recent years, the CO2 concentration has increased from historical levels of below 300 ppm to almost 400 ppm today (Figure \(\PageIndex{7}\)).
Summary
The ideal gas law can be used to derive a number of convenient equations relating directly measured quantities to properties of interest for gaseous substances and mixtures. Appropriate rearrangement of the ideal gas equation may be made to permit the calculation of gas densities and molar masses. Dalton’s law of partial pressures may be used to relate measured gas pressures for gaseous mixtures to their compositions. Avogadro’s law may be used in stoichiometric computations for chemical reactions involving gaseous reactants or products.
Key Equations
- PTotal = PA + PB + PC + … = ƩiPi
- PA = XA PTotal
- \(X_A=\dfrac{n_A}{n_{Total}}\)
Footnotes
- “Quotations by Joseph-Louis Lagrange,” last modified February 2006, accessed February 10, 2015, www-history.mcs.st-andrews.ac.../Lagrange.html
Summary
- Dalton’s law of partial pressures
- total pressure of a mixture of ideal gases is equal to the sum of the partial pressures of the component gases.
- mole fraction (X)
- concentration unit defined as the ratio of the molar amount of a mixture component to the total number of moles of all mixture components
- partial pressure
- pressure exerted by an individual gas in a mixture
- vapor pressure of water
- pressure exerted by water vapor in equilibrium with liquid water in a closed container at a specific temperature


