11.E: Solutions and Colloids (Exercises)
- Page ID
- 221211
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)11.2: The Dissolution Process
Q11.2.1
How do solutions differ from compounds? From other mixtures?
S11.2.1
A solution can vary in composition, while a compound cannot vary in composition. Solutions are homogeneous at the molecular level, while other mixtures are heterogeneous.
Q11.2.2
Which of the principal characteristics of solutions can we see in the solutions of \(\ce{K2Cr2O7}\) shown in

Figure: When potassium dichromate (\(\ce{K2Cr2O7}\)) is mixed with water, it forms a homogeneous orange solution. (credit: modification of work by Mark Ott)
S11.2.2
The solutions are the same throughout (the color is constant throughout), and the composition of a solution of K2Cr2O7 in water can vary.
Q11.2.3
When KNO3 is dissolved in water, the resulting solution is significantly colder than the water was originally.
- Is the dissolution of KNO3 an endothermic or an exothermic process?
- What conclusions can you draw about the intermolecular attractions involved in the process?
- Is the resulting solution an ideal solution?
S11.2.3
(a) The process is endothermic as the solution is consuming heat. (b) Attraction between the K+ and \(\ce{NO3-}\) ions is stronger than between the ions and water molecules (the ion-ion interactions have a lower, more negative energy). Therefore, the dissolution process increases the energy of the molecular interactions, and it consumes the thermal energy of the solution to make up for the difference. (c) No, an ideal solution is formed with no appreciable heat release or consumption.
Q11.2.4
Give an example of each of the following types of solutions:
- a gas in a liquid
- a gas in a gas
- a solid in a solid
S11.2.4
(a) CO2 in water; (b) O2 in N2 (air); (c) bronze (solution of tin or other metals in copper)
Q11.2.5
Indicate the most important types of intermolecular attractions in each of the following solutions:
- The solution in Figure.
- NO(l) in CO(l)
- Cl2(g) in Br2(l)
- HCl(aq) in benzene C6H6(l)
- Methanol CH3OH(l) in H2O(l)
S11.2.5
(a) ion-dipole forces; (b) dipole-dipole forces; (c) dispersion forces; (d) dispersion forces; (e) hydrogen bonding
Q11.2.5
Predict whether each of the following substances would be more soluble in water (polar solvent) or in a hydrocarbon such as heptane (C7H16, nonpolar solvent):
- vegetable oil (nonpolar)
- isopropyl alcohol (polar)
- potassium bromide (ionic)
S11.2.5
(a) heptane; (b) water; (c) water
Q11.2.6
Heat is released when some solutions form; heat is absorbed when other solutions form. Provide a molecular explanation for the difference between these two types of spontaneous processes.
S11.2.6
Heat is released when the total intermolecular forces (IMFs) between the solute and solvent molecules are stronger than the total IMFs in the pure solute and in the pure solvent: Breaking weaker IMFs and forming stronger IMFs releases heat. Heat is absorbed when the total IMFs in the solution are weaker than the total of those in the pure solute and in the pure solvent: Breaking stronger IMFs and forming weaker IMFs absorbs heat.
Q11.2.7
Solutions of hydrogen in palladium may be formed by exposing Pd metal to H2 gas. The concentration of hydrogen in the palladium depends on the pressure of H2 gas applied, but in a more complex fashion than can be described by Henry’s law. Under certain conditions, 0.94 g of hydrogen gas is dissolved in 215 g of palladium metal.
- Determine the molarity of this solution (solution density = 1.8 g/cm3).
- Determine the molality of this solution (solution density = 1.8 g/cm3).
- Determine the percent by mass of hydrogen atoms in this solution (solution density = 1.8 g/cm3).
S11.2.7
http://cnx.org/contents/mH6aqegx@2/The-Dissolution-Process
11.3: Electrolytes
Q11.3.1
Explain why the ions Na+ and Cl− are strongly solvated in water but not in hexane, a solvent composed of nonpolar molecules.
S11.3.2
Crystals of NaCl dissolve in water, a polar liquid with a very large dipole moment, and the individual ions become strongly solvated. Hexane is a nonpolar liquid with a dipole moment of zero and, therefore, does not significantly interact with the ions of the NaCl crystals.
Q11.3.2
Explain why solutions of HBr in benzene (a nonpolar solvent) are nonconductive, while solutions in water (a polar solvent) are conductive.
S11.3.2
HBr is an acid and so its molecules react with water molecules to form H3O+ and Br− ions that provide conductivity to the solution. Though HBr is soluble in benzene, it does not react chemically but remains dissolved as neutral HBr molecules. With no ions present in the benzene solution, it is electrically nonconductive.
Q11.3.3
Consider the solutions presented:
(a) Which of the following sketches best represents the ions in a solution of Fe(NO3)3(aq)?
3_img.jpg?revision=1&size=bestfit&width=570&height=191)
(b) Write a balanced chemical equation showing the products of the dissolution of Fe(NO3)3.
S11.3.3
(a) Fe(NO3)3 is a strong electrolyte, thus it should completely dissociate into Fe3+ and \(\ce{(NO3- )}\) ions. Therefore, (z) best represents the solution. (b) \(\ce{Fe(NO3)3}(s)⟶\ce{Fe^3+}(aq)+\ce{3NO3- }(aq)\)
Q11.3.4
Compare the processes that occur when methanol (CH3OH), hydrogen chloride (HCl), and sodium hydroxide (NaOH) dissolve in water. Write equations and prepare sketches showing the form in which each of these compounds is present in its respective solution.
S11.3.3
Methanol, \(CH_3OH\), dissolves in water in all proportions, interacting via hydrogen bonding.
Methanol:
\[CH_3OH_{(l)}+H_2O_{(l)}⟶CH_3OH_{(aq)}\]

Hydrogen chloride, HCl, dissolves in and reacts with water to yield hydronium cations and chloride anions that are solvated by strong ion-dipole interactions.
Hydrogen chloride:
\[HCl{(g)}+H_2O_{(l)} \rightarrow H_3O^+_{(aq)}+Cl^−_{(aq)}\]
Sodium hydroxide, NaOH, dissolves in water and dissociates to yield sodium cations and hydroxide anions that are strongly solvated by ion-dipole interactions and hydrogen bonding, respectively.
Sodium hydroxide:
\[NaOH_{(s)} \rightarrow Na^+_{(aq)} + OH^−_{(aq)}\]

Q11.3.5
What is the expected electrical conductivity of the following solutions?
- NaOH(aq)
- HCl(aq)
- C6H12O6(aq) (glucose)
- NH3(l)
S11.3.5
(a) high conductivity (solute is an ionic compound that will dissociate when dissolved); (b) high conductivity (solute is a strong acid and will ionize completely when dissolved); (c) nonconductive (solute is a covalent compound, neither acid nor base, unreactive towards water); (d) low conductivity (solute is a weak base and will partially ionize when dissolved)
Q11.3.6
Why are most solid ionic compounds electrically nonconductive, whereas aqueous solutions of ionic compounds are good conductors? Would you expect a liquid (molten) ionic compound to be electrically conductive or nonconductive? Explain.
S11.3.6
A medium must contain freely mobile, charged entities to be electrically conductive. The ions present in a typical ionic solid are immobilized in a crystalline lattice and so the solid is not able to support an electrical current. When the ions are mobilized, either by melting the solid or dissolving it in water to dissociate the ions, current may flow and these forms of the ionic compound are conductive.
Q11.3.7
Indicate the most important type of intermolecular attraction responsible for solvation in each of the following solutions:
- the solutions in Figure
- methanol, CH3OH, dissolved in ethanol, C2H5OH
- methane, CH4, dissolved in benzene, C6H6
- the polar halocarbon CF2Cl2 dissolved in the polar halocarbon CF2ClCFCl2
- O2(l) in N2(l)
S11.3.7
(a) ion-dipole; (b) hydrogen bonds; (c) dispersion forces; (d) dipole-dipole attractions; (e) dispersion forces
11.4: Solubility
Q11.4.1
Suppose you are presented with a clear solution of sodium thiosulfate, Na2S2O3. How could you determine whether the solution is unsaturated, saturated, or supersaturated?
S11.4.1
Add a small crystal of \(Na_2S_2O_3\). It will dissolve in an unsaturated solution, remain apparently unchanged in a saturated solution, or initiate precipitation in a supersaturated solution.
Q11.4.2
Supersaturated solutions of most solids in water are prepared by cooling saturated solutions. Supersaturated solutions of most gases in water are prepared by heating saturated solutions. Explain the reasons for the difference in the two procedures.
S11.4.2
The solubility of solids usually decreases upon cooling a solution, while the solubility of gases usually decreases upon heating.
Q11.4.3
Suggest an explanation for the observations that ethanol, C2H5OH, is completely miscible with water and that ethanethiol, C2H5SH, is soluble only to the extent of 1.5 g per 100 mL of water.
S11.4.3
The hydrogen bonds between water and C2H5OH are much stronger than the intermolecular attractions between water and C2H5SH.
Q11.4.4
Calculate the percent by mass of KBr in a saturated solution of KBr in water at 10 °C using the following figure for useful data, and report the computed percentage to one significant digit.
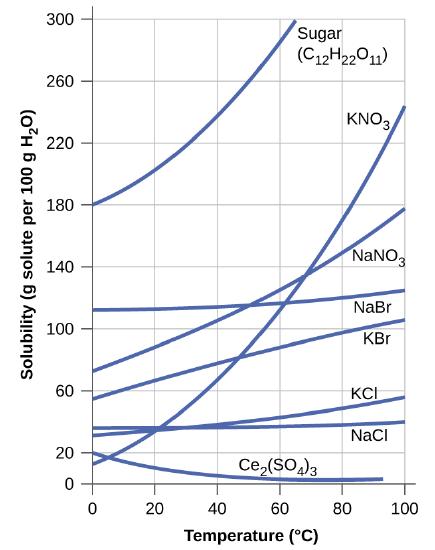
This graph shows how the solubility of several solids changes with temperature.
S11.4.4
At 10 °C, the solubility of KBr in water is approximately 60 g per 100 g of water.
\[\%\; KBr =\dfrac{60\; g\; KBr}{(60+100)\;g\; solution} = 40\%\]
Q11.4.5
Which of the following gases is expected to be most soluble in water? Explain your reasoning.
- CH4
- CCl4
- CHCl3
S11.4.5
(c) CHCl3 is expected to be most soluble in water. Of the three gases, only this one is polar and thus capable of experiencing relatively strong dipole-dipole attraction to water molecules.
Q11.4.6
At 0 °C and 1.00 atm, as much as 0.70 g of O2 can dissolve in 1 L of water. At 0 °C and 4.00 atm, how many grams of O2 dissolve in 1 L of water?
S11.4.6
This problem requires the application of Henry’s law. The governing equation is \(C_g = kP_g\).
\[k=\dfrac{C_g}{P_g}=\dfrac{0.70\;g}{1.00\; atm} =0.70\;g\; atm^{−1}\]
Under the new conditions, \(C_g=0.70\;g\;atm^{−1} \times 4.00\; atm = 2.80\; g\).
Q11.4.7
Refer to following figure for the following three questions:

- How did the concentration of dissolved CO2 in the beverage change when the bottle was opened?
- What caused this change?
- Is the beverage unsaturated, saturated, or supersaturated with CO2?
S11.4.7
(a) It decreased as some of the CO2 gas left the solution (evidenced by effervescence). (b) Opening the bottle released the high-pressure CO2 gas above the beverage. The reduced CO2 gas pressure, per Henry’s law, lowers the solubility for CO2. (c) The dissolved CO2 concentration will continue to slowly decrease until equilibrium is reestablished between the beverage and the very low CO2 gas pressure in the opened bottle. Immediately after opening, the beverage, therefore, contains dissolved CO2 at a concentration greater than its solubility, a nonequilibrium condition, and is said to be supersaturated.
Q11.4.8
The Henry’s law constant for CO2 is \(3.4 \times 10^{−2}\; M/atm\) at 25 °C. What pressure of carbon dioxide is needed to maintain a CO2 concentration of 0.10 M in a can of lemon-lime soda?
S11.4.8
\[P_g=\dfrac{C_g}{k}=\dfrac{0.10\; M}{3.4 \times 10^{−2}\;M/atm} =2.9\; atm\]
Q11.4.9
The Henry’s law constant for O2 is \(1.3\times 10^{−3}\; M/atm\) at 25 °C. What mass of oxygen would be dissolved in a 40-L aquarium at 25 °C, assuming an atmospheric pressure of 1.00 atm, and that the partial pressure of O2 is 0.21 atm?
S11.4.9
Start with Henry's law
\[C_g=kP_g\]
and apply it to \(O_2\)
\[C(O_2)=(1.3 \times 10^{−3}\; M/atm) (0.21\;atm)=2.7 \times 10^{−4}\;mol/L\]
The total amount is \((2.7 \times 10^{−4}\; mol/L)(40\;L=1.08 \times 10^{−2} \;mol\]
The mass of oxygen is \((1.08 \times 10^{−2}\; mol)(32.0\; g/mol)=0.346\;g\)
or, using two significant figures, \(0.35\; g\).
Q11.4.10
How many liters of HCl gas, measured at 30.0 °C and 745 torr, are required to prepare 1.25 L of a 3.20-M solution of hydrochloric acid?
S11.4.10
First, calculate the moles of HCl needed. Then use the ideal gas law to find the volume required.
M = mol L−1
3.20M=xmol1.25L
x = 4.00 mol HCl
Before using the ideal gas law, change pressure to atmospheres and convert temperature from °C to kelvin.
\[1\;atmx=760torr745torr
x = 0.9803 atm
V=nRTP=(4.000molHCl)(0.08206LatmK−1mol−1)(303.15K)0.9803atm=102 L HCl
102 L HCl
more http://cnx.org/contents/2488fW6W@2/Solubility
11.5: Colligative Properties
Q11.5.1
Which is/are part of the macroscopic domain of solutions and which is/are part of the microscopic domain: boiling point elevation, Henry’s law, hydrogen bond, ion-dipole attraction, molarity, nonelectrolyte, nonstoichiometric compound, osmosis, solvated ion?
Q11.5.2
What is the microscopic explanation for the macroscopic behavior illustrated in [link]?
S11.5.2
The strength of the bonds between like molecules is stronger than the strength between unlike molecules. Therefore, some regions will exist in which the water molecules will exclude oil molecules and other regions will exist in which oil molecules will exclude water molecules, forming a heterogeneous region.
Q11.5.3
Sketch a qualitative graph of the pressure versus time for water vapor above a sample of pure water and a sugar solution, as the liquids evaporate to half their original volume.
Q11.5.4
A solution of potassium nitrate, an electrolyte, and a solution of glycerin (C3H5(OH)3), a nonelectrolyte, both boil at 100.3 °C. What other physical properties of the two solutions are identical?
S11.5.4
Both form homogeneous solutions; their boiling point elevations are the same, as are their lowering of vapor pressures. Osmotic pressure and the lowering of the freezing point are also the same for both solutions.
Q11.5.5
What are the mole fractions of H3PO4 and water in a solution of 14.5 g of H3PO4 in 125 g of water?
Q11.5.6
What are the mole fractions of HNO3 and water in a concentrated solution of nitric acid (68.0% HNO3 by mass)?
S11.5.6
- Find number of moles of HNO3 and H2O in 100 g of the solution. Find the mole fractions for the components.
- The mole fraction of HNO3 is 0.378. The mole fraction of H2O is 0.622.
Q11.5.7
Calculate the mole fraction of each solute and solvent:
- 583 g of H2SO4 in 1.50 kg of water—the acid solution used in an automobile battery
- 0.86 g of NaCl in 1.00 × 102 g of water—a solution of sodium chloride for intravenous injection
- 46.85 g of codeine, C18H21NO3, in 125.5 g of ethanol, C2H5OH
- 25 g of I2 in 125 g of ethanol, C2H5OH
S11.5.7
a. \(583\:g\:\ce{H2SO4}\times\dfrac{1\:mole\:\ce{H2SO4}}{98.08\:g\:\ce{H2SO4}}=5.94\:mole\:\ce{H2SO4}\) \(\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\) \(1.50\:kg\:\ce{H2O}\times\dfrac{1000\:g}{1\:kg}\times\dfrac{1\:mole\:\ce{H2O}}{18.02\:g\:\ce{H2O}}=83.2\:moles\:\ce{H2O}\)
Q11.5.8
Calculate the mole fraction of each solute and solvent:
- 0.710 kg of sodium carbonate (washing soda), Na2CO3, in 10.0 kg of water—a saturated solution at 0 °C
- 125 g of NH4NO3 in 275 g of water—a mixture used to make an instant ice pack
- 25 g of Cl2 in 125 g of dichloromethane, CH2Cl2
- 0.372 g of histamine, C5H9N, in 125 g of chloroform, CHCl3
S11.5.8
- \(X_\mathrm{Na_2CO_3}=0.0119\); \(X_\mathrm{H_2O}=0.988\);
- \(X_\mathrm{NH_4NO_3}=0.9927\); \(X_\mathrm{H_2O}=0.907\);
- \(X_\mathrm{Cl_2}=0.192\); \(X_\mathrm{CH_2CI_2}=0.808\);
- \(X_\mathrm{C_5H_9N}=0.00426\); \(X_\mathrm{CHCl_3}=0.997\)
Q11.5.9
Calculate the mole fractions of methanol, CH3OH; ethanol, C2H5OH; and water in a solution that is 40% methanol, 40% ethanol, and 20% water by mass. (Assume the data are good to two significant figures.)
Q11.5.10
What is the difference between a 1 M solution and a 1 m solution?
S11.5.10
In a 1 M solution, the mole is contained in exactly 1 L of solution. In a 1 m solution, the mole is contained in exactly 1 kg of solvent.
Q11.5.11
What is the molality of phosphoric acid, H3PO4, in a solution of 14.5 g of H3PO4 in 125 g of water?
Q11.5.12
What is the molality of nitric acid in a concentrated solution of nitric acid (68.0% HNO3 by mass)?
S11.5.12
(a) Determine the molar mass of HNO3. Determine the number of moles of acid in the solution. From the number of moles and the mass of solvent, determine the molality. (b) 33.7 m
Q11.5.13
Calculate the molality of each of the following solutions:
- 583 g of H2SO4 in 1.50 kg of water—the acid solution used in an automobile battery
- 0.86 g of NaCl in 1.00 × 102 g of water—a solution of sodium chloride for intravenous injection
- 46.85 g of codeine, C18H21NO3, in 125.5 g of ethanol, C2H5OH
- 25 g of I2 in 125 g of ethanol, C2H5OH
Q11.5.14
Calculate the molality of each of the following solutions:
- 0.710 kg of sodium carbonate (washing soda), Na2CO3, in 10.0 kg of water—a saturated solution at 0°C
- 125 g of NH4NO3 in 275 g of water—a mixture used to make an instant ice pack
- 25 g of Cl2 in 125 g of dichloromethane, CH2Cl2
- 0.372 g of histamine, C5H9N, in 125 g of chloroform, CHCl3
S11.5.14
(a) 6.70 × 10−1 m; (b) 5.67 m; (c) 2.8 m; (d) 0.0358 m
Q11.5.15
The concentration of glucose, C6H12O6, in normal spinal fluid is \(\mathrm{\dfrac{75\:mg}{100\:g}}\). What is the molality of the solution?
Q11.5.16
A 13.0% solution of K2CO3 by mass has a density of 1.09 g/cm3. Calculate the molality of the solution.
S11.5.16
1.08 m
Q11.5.17
- Why does 1 mol of sodium chloride depress the freezing point of 1 kg of water almost twice as much as 1 mol of glycerin?
- What is the boiling point of a solution of 115.0 g of sucrose, C12H22O11, in 350.0 g of water?
S11.5.17
- Determine the molar mass of sucrose; determine the number of moles of sucrose in the solution; convert the mass of solvent to units of kilograms; from the number of moles and the mass of solvent, determine the molality; determine the difference between the boiling point of water and the boiling point of the solution; determine the new boiling point.
- 100.5 °C
Q11.5.18
What is the boiling point of a solution of 9.04 g of I2 in 75.5 g of benzene, assuming the I2 is nonvolatile?
Q11.5.19
What is the freezing temperature of a solution of 115.0 g of sucrose, C12H22O11, in 350.0 g of water, which freezes at 0.0 °C when pure?
S11.5.19
(a) Determine the molar mass of sucrose; determine the number of moles of sucrose in the solution; convert the mass of solvent to units of kilograms; from the number of moles and the mass of solvent, determine the molality; determine the difference between the freezing temperature of water and the freezing temperature of the solution; determine the new freezing temperature. (b) −1.8 °C
Q11.5.20
What is the freezing point of a solution of 9.04 g of I2 in 75.5 g of benzene?
Q11.5.21
What is the osmotic pressure of an aqueous solution of 1.64 g of Ca(NO3)2 in water at 25 °C? The volume of the solution is 275 mL.
S11.5.21
(a) Determine the molar mass of Ca(NO3)2; determine the number of moles of Ca(NO3)2 in the solution; determine the number of moles of ions in the solution; determine the molarity of ions, then the osmotic pressure. (b) 2.67 atm
Q11.5.22
What is osmotic pressure of a solution of bovine insulin (molar mass, 5700 g mol−1) at 18 °C if 100.0 mL of the solution contains 0.103 g of the insulin?
Q11.5.23
What is the molar mass of a solution of 5.00 g of a compound in 25.00 g of carbon tetrachloride (bp 76.8 °C; Kb = 5.02 °C/m) that boils at 81.5 °C at 1 atm?
S11.5.24
(a) Determine the molal concentration from the change in boiling point and Kb; determine the moles of solute in the solution from the molal concentration and mass of solvent; determine the molar mass from the number of moles and the mass of solute. (b) 2.1 × 102 g mol−1
Q11.5.25
A sample of an organic compound (a nonelectrolyte) weighing 1.35 g lowered the freezing point of 10.0 g of benzene by 3.66 °C. Calculate the molar mass of the compound.
Q11.5.26
A 1.0 m solution of HCl in benzene has a freezing point of 0.4 °C. Is HCl an electrolyte in benzene? Explain.
S11.5.26
No. Pure benzene freezes at 5.5 °C, and so the observed freezing point of this solution is depressed by ΔTf = 5.5 − 0.4 = 5.1 °C. The value computed, assuming no ionization of HCl, is ΔTf = (1.0 m)(5.14 °C/m) = 5.1 °C. Agreement of these values supports the assumption that HCl is not ionized.
Q11.5.27
A solution contains 5.00 g of urea, CO(NH2)2, a nonvolatile compound, dissolved in 0.100 kg of water. If the vapor pressure of pure water at 25 °C is 23.7 torr, what is the vapor pressure of the solution?
Q11.5.28
A 12.0-g sample of a nonelectrolyte is dissolved in 80.0 g of water. The solution freezes at −1.94 °C. Calculate the molar mass of the substance.
S11.5.28
144 g mol−1
Q11.5.29
Arrange the following solutions in order by their decreasing freezing points: 0.1 m Na3PO4, 0.1 m C2H5OH, 0.01 m CO2, 0.15 m NaCl, and 0.2 m CaCl2.
Q11.5.30
Calculate the boiling point elevation of 0.100 kg of water containing 0.010 mol of NaCl, 0.020 mol of Na2SO4, and 0.030 mol of MgCl2, assuming complete dissociation of these electrolytes.
S11.5.30
0.870 °C
Q11.5.31
How could you prepare a 3.08 m aqueous solution of glycerin, C3H8O3? What is the freezing point of this solution?
Q11.5.32
A sample of sulfur weighing 0.210 g was dissolved in 17.8 g of carbon disulfide, CS2 (Kb = 2.43 °C/m). If the boiling point elevation was 0.107 °C, what is the formula of a sulfur molecule in carbon disulfide?
S11.5.32
S8
Q11.5.33
In a significant experiment performed many years ago, 5.6977 g of cadmium iodide in 44.69 g of water raised the boiling point 0.181 °C. What does this suggest about the nature of a solution of CdI2?
Q11.5.34
Lysozyme is an enzyme that cleaves cell walls. A 0.100-L sample of a solution of lysozyme that contains 0.0750 g of the enzyme exhibits an osmotic pressure of 1.32 × 10−3 atm at 25 °C. What is the molar mass of lysozyme?
S11.5.34
1.39 × 104 g mol−1
Q11.5.35
The osmotic pressure of a solution containing 7.0 g of insulin per liter is 23 torr at 25 °C. What is the molar mass of insulin?
Q11.5.36
The osmotic pressure of human blood is 7.6 atm at 37 °C. What mass of glucose, C6H12O6, is required to make 1.00 L of aqueous solution for intravenous feeding if the solution must have the same osmotic pressure as blood at body temperature, 37 °C?
S11.5.36
54 g
Q11.5.37
What is the freezing point of a solution of dibromobenzene, C6H4Br2, in 0.250 kg of benzene, if the solution boils at 83.5 °C?
Q11.5.38
What is the boiling point of a solution of NaCl in water if the solution freezes at −0.93 °C?
S11.5.38
100.26 °C
Q11.5.39
The sugar fructose contains 40.0% C, 6.7% H, and 53.3% O by mass. A solution of 11.7 g of fructose in 325 g of ethanol has a boiling point of 78.59 °C. The boiling point of ethanol is 78.35 °C, and Kb for ethanol is 1.20 °C/m. What is the molecular formula of fructose?
Q11.5.40
The vapor pressure of methanol, CH3OH, is 94 torr at 20 °C. The vapor pressure of ethanol, C2H5OH, is 44 torr at the same temperature.
- Calculate the mole fraction of methanol and of ethanol in a solution of 50.0 g of methanol and 50.0 g of ethanol.
- Ethanol and methanol form a solution that behaves like an ideal solution. Calculate the vapor pressure of methanol and of ethanol above the solution at 20 °C.
- Calculate the mole fraction of methanol and of ethanol in the vapor above the solution.
S11.5.40
(a) \(X_\mathrm{CH_3OH}=0.590\); \(X_\mathrm{C_2H_5OH}=0.410\); (b) Vapor pressures are: CH3OH: 55 torr; C2H5OH: 18 torr; (c) CH3OH: 0.75; C2H5OH: 0.25
Q11.5.41
The triple point of air-free water is defined as 273.15 K. Why is it important that the water be free of air?
Q11.5.42
Meat can be classified as fresh (not frozen) even though it is stored at −1 °C. Why wouldn’t meat freeze at this temperature?
S11.5.42
The ions and compounds present in the water in the beef lower the freezing point of the beef below −1 °C.
Q11.5.43
An organic compound has a composition of 93.46% C and 6.54% H by mass. A solution of 0.090 g of this compound in 1.10 g of camphor melts at 158.4 °C. The melting point of pure camphor is 178.4 °C. Kf for camphor is 37.7 °C/m. What is the molecular formula of the solute? Show your calculations.
Q11.5.44
A sample of HgCl2 weighing 9.41 g is dissolved in 32.75 g of ethanol, C2H5OH (Kb = 1.20 °C/m). The boiling point elevation of the solution is 1.27 °C. Is HgCl2 an electrolyte in ethanol? Show your calculations.
S11.5.44
\(\mathrm{Δbp}=K_\ce{b}m=(1.20\:°\ce C/m)\mathrm{\left(\dfrac{9.41\:g×\dfrac{1\:mol\: HgCl_2}{271.496\:g}}{0.03275\:kg}\right)=1.27\:°\ce C}\)
The observed change equals the theoretical change; therefore, no dissociation occurs.
Q11.5.45
A salt is known to be an alkali metal fluoride. A quick approximate determination of freezing point indicates that 4 g of the salt dissolved in 100 g of water produces a solution that freezes at about −1.4 °C. What is the formula of the salt? Show your calculations.
11.6: Colloids
Q11.6.1
Identify the dispersed phase and the dispersion medium in each of the following colloidal systems: starch dispersion, smoke, fog, pearl, whipped cream, floating soap, jelly, milk, and ruby.
S11.6.1
| Colloidal System | Dispersed Phase | Dispersion Medium |
|---|---|---|
| starch dispersion | starch | water |
| smoke | solid particles | air |
| fog | water | air |
| pearl | water | calcium carbonate (CaCO3) |
| whipped cream | air | cream |
| floating soap | air | soap |
| jelly | fruit juice | pectin gel |
| milk | butterfat | water |
| ruby | chromium(III) oxide (Cr2O3) | aluminum oxide (Al2O3) |
Q11.6.2
Distinguish between dispersion methods and condensation methods for preparing colloidal systems.
S11.6.2
Dispersion methods use a grinding device or some other means to bring about the subdivision of larger particles. Condensation methods bring smaller units together to form a larger unit. For example, water molecules in the vapor state come together to form very small droplets that we see as clouds.
Q11.6.3
How do colloids differ from solutions with regard to dispersed particle size and homogeneity?
S11.6.3
Colloidal dispersions consist of particles that are much bigger than the solutes of typical solutions. Colloidal particles are either very large molecules or aggregates of smaller species that usually are big enough to scatter light. Colloids are homogeneous on a macroscopic (visual) scale, while solutions are homogeneous on a microscopic (molecular) scale.
Q11.6.4
Explain the cleansing action of soap.
S11.6.4
Soap molecules have both a hydrophobic and a hydrophilic end. The charged (hydrophilic) end, which is usually associated with an alkali metal ion, ensures water solubility The hydrophobic end permits attraction to oil, grease, and other similar nonpolar substances that normally do not dissolve in water but are pulled into the solution by the soap molecules.
Q11.6.5
How can it be demonstrated that colloidal particles are electrically charged?
S11.6.5
If they are placed in an electrolytic cell, dispersed particles will move toward the electrode that carries a charge opposite to their own charge. At this electrode, the charged particles will be neutralized and will coagulate as a precipitate.
Contributors and Attributions
Paul Flowers (University of North Carolina - Pembroke), Klaus Theopold (University of Delaware) and Richard Langley (Stephen F. Austin State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110).


