10.E: Liquids and Solids (Exercises)
- Page ID
- 221203
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)10.1: Intermolecular Forces
Q10.1.1
In terms of their bulk properties, how do liquids and solids differ? How are they similar?
S10.1.1
Liquids and solids are similar in that they are matter composed of atoms, ions, or molecules. They are incompressible and have similar densities that are both much larger than those of gases. They are different in that liquids have no fixed shape, and solids are rigid.
Q10.1.2
In terms of the kinetic molecular theory, in what ways are liquids similar to solids? In what ways are liquids different from solids?
Q10.1.3
In terms of the kinetic molecular theory, in what ways are liquids similar to gases? In what ways are liquids different from gases?
S10.1.3
They are similar in that the atoms or molecules are free to move from one position to another. They differ in that the particles of a liquid are confined to the shape of the vessel in which they are placed. In contrast, a gas will expand without limit to fill the space into which it is placed.
Q10.1.4
Explain why liquids assume the shape of any container into which they are poured, whereas solids are rigid and retain their shape.
Q10.1.5
What is the evidence that all neutral atoms and molecules exert attractive forces on each other?
S10.1.5
All atoms and molecules will condense into a liquid or solid in which the attractive forces exceed the kinetic energy of the molecules, at sufficiently low temperature.
Q10.1.6
Open the PhET States of Matter Simulation to answer the following questions:
- Select the Solid, Liquid, Gas tab. Explore by selecting different substances, heating and cooling the systems, and changing the state. What similarities do you notice between the four substances for each phase (solid, liquid, gas)? What differences do you notice?
- For each substance, select each of the states and record the given temperatures. How do the given temperatures for each state correlate with the strengths of their intermolecular attractions? Explain.
- Select the Interaction Potential tab, and use the default neon atoms. Move the Ne atom on the right and observe how the potential energy changes. Select the Total Force button, and move the Ne atom as before. When is the total force on each atom attractive and large enough to matter? Then select the Component Forces button, and move the Ne atom. When do the attractive (van der Waals) and repulsive (electron overlap) forces balance? How does this relate to the potential energy versus the distance between atoms graph? Explain.
Q10.1.7
Define the following and give an example of each:
- dispersion force
- dipole-dipole attraction
- hydrogen bond
S10.1.7
- Dispersion forces occur as an atom develops a temporary dipole moment when its electrons are distributed asymmetrically about the nucleus. This structure is more prevalent in large atoms such as argon or radon. A second atom can then be distorted by the appearance of the dipole in the first atom. The electrons of the second atom are attracted toward the positive end of the first atom, which sets up a dipole in the second atom. The net result is rapidly fluctuating, temporary dipoles that attract one another (example: Ar).
- A dipole-dipole attraction is a force that results from an electrostatic attraction of the positive end of one polar molecule for the negative end of another polar molecule (example: ICI molecules attract one another by dipole-dipole interaction).
- Hydrogen bonds form whenever a hydrogen atom is bonded to one of the more electronegative atoms, such as a fluorine, oxygen, nitrogen, or chlorine atom. The electrostatic attraction between the partially positive hydrogen atom in one molecule and the partially negative atom in another molecule gives rise to a strong dipole-dipole interaction called a hydrogen bond (example: \(\mathrm{HF⋯HF}\)).
Q10.1.8
The types of intermolecular forces in a substance are identical whether it is a solid, a liquid, or a gas. Why then does a substance change phase from a gas to a liquid or to a solid?
Q10.1.9
Why do the boiling points of the noble gases increase in the order He < Ne < Ar < Kr < Xe?
S10.1.9
The London forces typically increase as the number of electrons increase.
Q10.1.10
Neon and HF have approximately the same molecular masses.
- Explain why the boiling points of Neon and HF differ.
- Compare the change in the boiling points of Ne, Ar, Kr, and Xe with the change of the boiling points of HF, HCl, HBr, and HI, and explain the difference between the changes with increasing atomic or molecular mass.
Q10.1.11
Arrange each of the following sets of compounds in order of increasing boiling point temperature:
- HCl, H2O, SiH4
- F2, Cl2, Br2
- CH4, C2H6, C3H8
- O2, NO, N2
S10.1.11
(a) SiH4 < HCl < H2O; (b) F2 < Cl2 < Br2; (c) CH4 < C2H6 < C3H8; (d) N2 < O2 < NO
Q10.1.12
The molecular mass of butanol, C4H9OH, is 74.14; that of ethylene glycol, CH2(OH)CH2OH, is 62.08, yet their boiling points are 117.2 °C and 174 °C, respectively. Explain the reason for the difference.
Q10.1.13
On the basis of intermolecular attractions, explain the differences in the boiling points of n–butane (−1 °C) and chloroethane (12 °C), which have similar molar masses.
S10.1.13
Only rather small dipole-dipole interactions from C-H bonds are available to hold n-butane in the liquid state. Chloroethane, however, has rather large dipole interactions because of the Cl-C bond; the interaction is therefore stronger, leading to a higher boiling point.
Q10.1.14
On the basis of dipole moments and/or hydrogen bonding, explain in a qualitative way the differences in the boiling points of acetone (56.2 °C) and 1-propanol (97.4 °C), which have similar molar masses.
Q10.1.15
The melting point of H2O(s) is 0 °C. Would you expect the melting point of H2S(s) to be −85 °C, 0 °C, or 185 °C? Explain your answer.
S10.1.15
−85 °C. Water has stronger hydrogen bonds so it melts at a higher temperature.
Q10.1.16
Silane (SiH4), phosphine (PH3), and hydrogen sulfide (H2S) melt at −185 °C, −133 °C, and −85 °C, respectively. What does this suggest about the polar character and intermolecular attractions of the three compounds?
Q10.1.17
Explain why a hydrogen bond between two water molecules is weaker than a hydrogen bond between two hydrogen fluoride molecules.
S10.1.17
The hydrogen bond between two hydrogen fluoride molecules is stronger than that between two water molecules because the electronegativity of F is greater than that of O. Consequently, the partial negative charge on F is greater than that on O. The hydrogen bond between the partially positive H and the larger partially negative F will be stronger than that formed between H and O.
Q10.1.18
Under certain conditions, molecules of acetic acid, CH3COOH, form “dimers,” pairs of acetic acid molecules held together by strong intermolecular attractions:
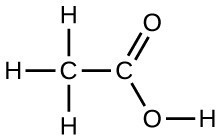
Draw a dimer of acetic acid, showing how two CH3COOH molecules are held together, and stating the type of IMF that is responsible.
Q10.1.19
Proteins are chains of amino acids that can form in a variety of arrangements, one of which is a helix. What kind of IMF is responsible for holding the protein strand in this shape? On the protein image, show the locations of the IMFs that hold the protein together:
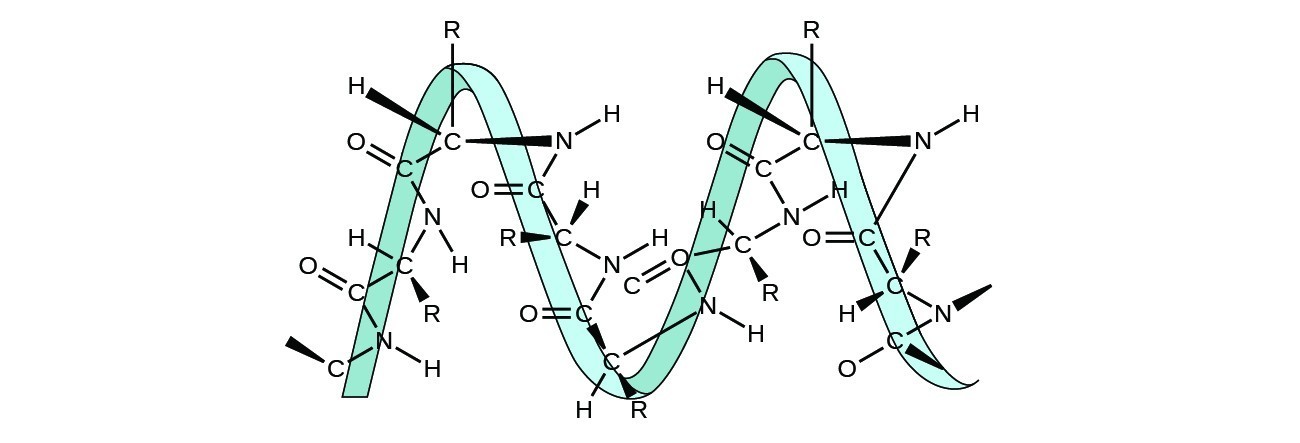
S10.1.19
H-bonding is the principle IMF holding the DNA strands together. The H-bonding is between the \(\mathrm{N−H}\) and \(\mathrm{C=O}\).
Q10.1.20
The density of liquid NH3 is 0.64 g/mL; the density of gaseous NH3 at STP is 0.0007 g/mL. Explain the difference between the densities of these two phases.
Q10.1.21
Identify the intermolecular forces present in the following solids:
- CH3CH2OH
- CH3CH2CH3
- CH3CH2Cl
S10.1.21
(a) hydrogen bonding and dispersion forces; (b) dispersion forces; (c) dipole-dipole attraction and dispersion forces
10.2: Properties of Liquids
Q10.2.1
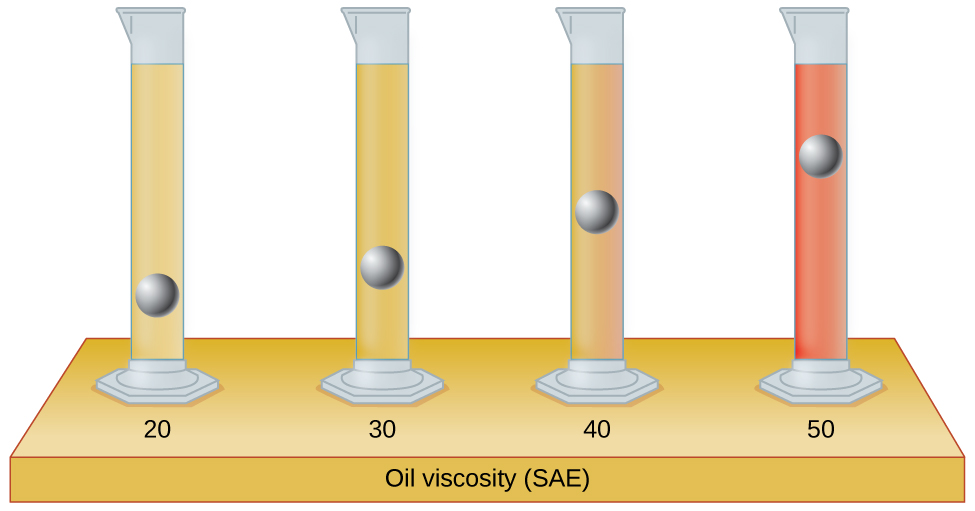
The test tubes shown here contain equal amounts of the specified motor oils. Identical metal spheres were dropped at the same time into each of the tubes, and a brief moment later, the spheres had fallen to the heights indicated in the illustration. Rank the motor oils in order of increasing viscosity, and explain your reasoning:
Q10.2.2
Although steel is denser than water, a steel needle or paper clip placed carefully lengthwise on the surface of still water can be made to float. Explain at a molecular level how this is possible:

(credit: Cory Zanker)
S10.2.2
The water molecules have strong intermolecular forces of hydrogen bonding. The water molecules are thus attracted strongly to one another and exhibit a relatively large surface tension, forming a type of “skin” at its surface. This skin can support a bug or paper clip if gently placed on the water.
Q10.2.3
The surface tension and viscosity values for diethyl ether, acetone, ethanol, and ethylene glycol are shown here.
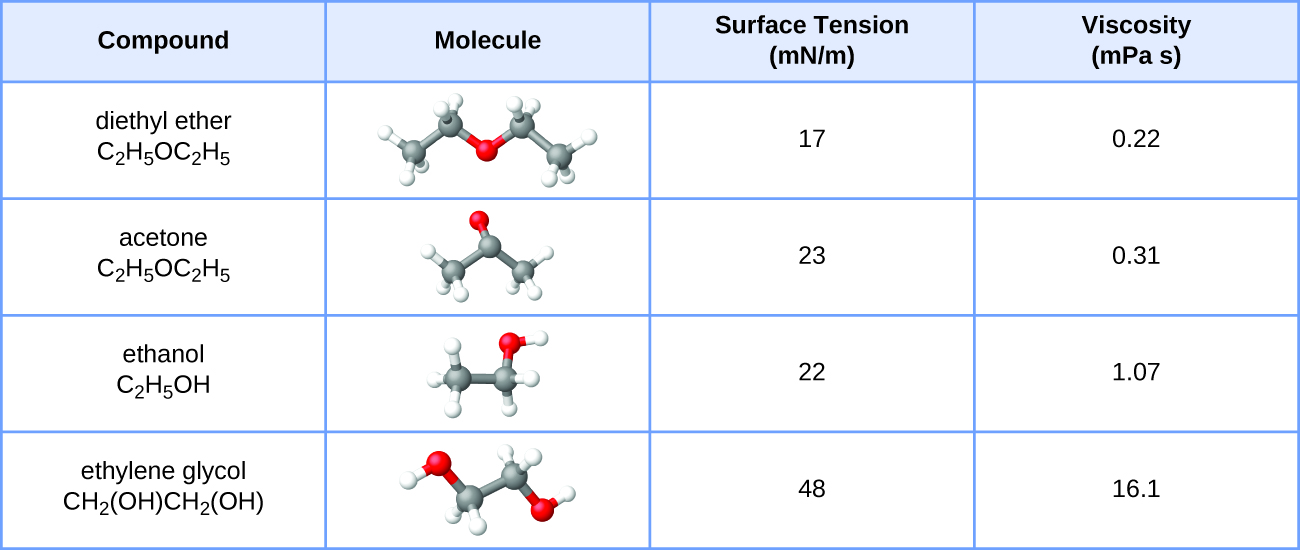
- Explain their differences in viscosity in terms of the size and shape of their molecules and their IMFs.
- Explain their differences in surface tension in terms of the size and shape of their molecules and their IMFs:
Q10.2.4
You may have heard someone use the figure of speech “slower than molasses in winter” to describe a process that occurs slowly. Explain why this is an apt idiom, using concepts of molecular size and shape, molecular interactions, and the effect of changing temperature.
S10.2.4
Temperature has an effect on intermolecular forces: the higher the temperature, the greater the kinetic energies of the molecules and the greater the extent to which their intermolecular forces are overcome, and so the more fluid (less viscous) the liquid; the lower the temperature, the lesser the intermolecular forces are overcome, and so the less viscous the liquid.
Q10.2.5
It is often recommended that you let your car engine run idle to warm up before driving, especially on cold winter days. While the benefit of prolonged idling is dubious, it is certainly true that a warm engine is more fuel efficient than a cold one. Explain the reason for this.
Q10.2.6
The surface tension and viscosity of water at several different temperatures are given in this table.
| Water | Surface Tension (mN/m) | Viscosity (mPa s) |
|---|---|---|
| 0 °C | 75.6 | 1.79 |
| 20 °C | 72.8 | 1.00 |
| 60 °C | 66.2 | 0.47 |
| 100 °C | 58.9 | 0.28 |
- As temperature increases, what happens to the surface tension of water? Explain why this occurs, in terms of molecular interactions and the effect of changing temperature.
- As temperature increases, what happens to the viscosity of water? Explain why this occurs, in terms of molecular interactions and the effect of changing temperature.
S10.2.6
(a) As the water reaches higher temperatures, the increased kinetic energies of its molecules are more effective in overcoming hydrogen bonding, and so its surface tension decreases. Surface tension and intermolecular forces are directly related. (b) The same trend in viscosity is seen as in surface tension, and for the same reason.
Q10.2.7
At 25 °C, how high will water rise in a glass capillary tube with an inner diameter of 0.63 mm? Refer to Example for the required information.
Q10.2.8
Water rises in a glass capillary tube to a height of 17 cm. What is the diameter of the capillary tube?
S10.2.8
9.5 × 10−5 m
10.3: Phase Transitions
Q10.3.1
Heat is added to boiling water. Explain why the temperature of the boiling water does not change. What does change?
Q10.3.2
Heat is added to ice at 0 °C. Explain why the temperature of the ice does not change. What does change?
S10.3.2
The heat is absorbed by the ice, providing the energy required to partially overcome intermolecular attractive forces in the solid and causing a phase transition to liquid water. The solution remains at 0 °C until all the ice is melted. Only the amount of water existing as ice changes until the ice disappears. Then the temperature of the water can rise.
Q10.3.3
What feature characterizes the dynamic equilibrium between a liquid and its vapor in a closed container?
Q10.3.4
Identify two common observations indicating some liquids have sufficient vapor pressures to noticeably evaporate?
S10.3.4
We can see the amount of liquid in an open container decrease and we can smell the vapor of some liquids.
Q10.3.5
Identify two common observations indicating some solids, such as dry ice and mothballs, have vapor pressures sufficient to sublime?
Q10.3.6
What is the relationship between the intermolecular forces in a liquid and its vapor pressure?
S10.3.7
The vapor pressure of a liquid decreases as the strength of its intermolecular forces increases.
Q10.3.7
What is the relationship between the intermolecular forces in a solid and its melting temperature?
Q10.3.8
Why does spilled gasoline evaporate more rapidly on a hot day than on a cold day?
S10.3.8
As the temperature increases, the average kinetic energy of the molecules of gasoline increases and so a greater fraction of molecules have sufficient energy to escape from the liquid than at lower temperatures.
Q10.3.9
Carbon tetrachloride, CCl4, was once used as a dry cleaning solvent, but is no longer used because it is carcinogenic. At 57.8 °C, the vapor pressure of CCl4 is 54.0 kPa, and its enthalpy of vaporization is 33.05 kJ/mol. Use this information to estimate the normal boiling point for CCl4.
Q10.3.10
When is the boiling point of a liquid equal to its normal boiling point?
S10.3.10
When the pressure of gas above the liquid is exactly 1 atm
Q10.3.11
How does the boiling of a liquid differ from its evaporation?
Q10.3.12
Use the information in Figure to estimate the boiling point of water in Denver when the atmospheric pressure is 83.3 kPa.
S10.3.12
approximately 95 °C
Q10.3.13
A syringe at a temperature of 20 °C is filled with liquid ether in such a way that there is no space for any vapor. If the temperature is kept constant and the plunger is withdrawn to create a volume that can be occupied by vapor, what would be the approximate pressure of the vapor produced?
Q10.3.14
Explain the following observations:
- It takes longer to cook an egg in Ft. Davis, Texas (altitude, 5000 feet above sea level) than it does in Boston (at sea level).
- Perspiring is a mechanism for cooling the body.
S10.3.14
(a) At 5000 feet, the atmospheric pressure is lower than at sea level, and water will therefore boil at a lower temperature. This lower temperature will cause the physical and chemical changes involved in cooking the egg to proceed more slowly, and a longer time is required to fully cook the egg. (b) As long as the air surrounding the body contains less water vapor than the maximum that air can hold at that temperature, perspiration will evaporate, thereby cooling the body by removing the heat of vaporization required to vaporize the water.
Q10.3.15
The enthalpy of vaporization of water is larger than its enthalpy of fusion. Explain why.
Q10.3.16
Explain why the molar enthalpies of vaporization of the following substances increase in the order CH4 < C2H6 < C3H8, even though all three substances experience the same dispersion forces when in the liquid state.
S10.3.16
Dispersion forces increase with molecular mass or size. As the number of atoms composing the molecules in this homologous series increases, so does the extent of intermolecular attraction via dispersion forces and, consequently, the energy required to overcome these forces and vaporize the liquids.
Q10.3.17
Explain why the enthalpies of vaporization of the following substances increase in the order CH4 < NH3 < H2O, even though all three substances have approximately the same molar mass.
Q10.3.18
The enthalpy of vaporization of CO2(l) is 9.8 kJ/mol. Would you expect the enthalpy of vaporization of CS2(l) to be 28 kJ/mol, 9.8 kJ/mol, or −8.4 kJ/mol? Discuss the plausibility of each of these answers.
S10.3.18
The boiling point of CS2 is higher than that of CO2 partially because of the higher molecular weight of CS2; consequently, the attractive forces are stronger in CS2. It would be expected, therefore, that the heat of vaporization would be greater than that of 9.8 kJ/mol for CO2. A value of 28 kJ/mol would seem reasonable. A value of −8.4 kJ/mol would indicate a release of energy upon vaporization, which is clearly implausible.
Q10.3.19
The hydrogen fluoride molecule, HF, is more polar than a water molecule, H2O (for example, has a greater dipole moment), yet the molar enthalpy of vaporization for liquid hydrogen fluoride is lesser than that for water. Explain.
Q10.3.20
Ethyl chloride (boiling point, 13 °C) is used as a local anesthetic. When the liquid is sprayed on the skin, it cools the skin enough to freeze and numb it. Explain the cooling effect of liquid ethyl chloride.
S10.3.20
The thermal energy (heat) needed to evaporate the liquid is removed from the skin.
Q10.3.21
Which contains the compounds listed correctly in order of increasing boiling points?
- N2 < CS2 < H2O < KCl
- H2O < N2 < CS2 < KCl
- N2 < KCl < CS2 < H2O
- CS2 < N2 < KCl < H2O
- KCl < H2O < CS2 < N2
Q10.3.22
How much heat is required to convert 422 g of liquid H2O at 23.5 °C into steam at 150 °C?
S10.3.22
1130 kJ
Q10.3.22
Evaporation of sweat requires energy and thus take excess heat away from the body. Some of the water that you drink may eventually be converted into sweat and evaporate. If you drink a 20-ounce bottle of water that had been in the refrigerator at 3.8 °C, how much heat is needed to convert all of that water into sweat and then to vapor?? (Note: Your body temperature is 36.6 °C. For the purpose of solving this problem, assume that the thermal properties of sweat are the same as for water.)
Q10.3.24
Titanium tetrachloride, TiCl4, has a melting point of −23.2 °C and has a ΔH fusion = 9.37 kJ/mol.
- How much energy is required to melt 263.1 g TiCl4?
- For TiCl4, which will likely have the larger magnitude: ΔH fusion or ΔH vaporization? Explain your reasoning.
S10.3.24
(a) 13.0 kJ; (b) It is likely that the heat of vaporization will have a larger magnitude since in the case of vaporization the intermolecular interactions have to be completely overcome, while melting weakens or destroys only some of them.
10.4: Phase Diagrams
Q10.4.1
From the phase diagram for water, determine the state of water at:
- 35 °C and 85 kPa
- −15 °C and 40 kPa
- −15 °C and 0.1 kPa
- 75 °C and 3 kPa
- 40 °C and 0.1 kPa
- 60 °C and 50 kPa
Q10.4.2
What phase changes will take place when water is subjected to varying pressure at a constant temperature of 0.005 °C? At 40 °C? At −40 °C?
S10.4.2
At low pressures and 0.005 °C, the water is a gas. As the pressure increases to 4.6 torr, the water becomes a solid; as the pressure increases still more, it becomes a liquid. At 40 °C, water at low pressure is a vapor; at pressures higher than about 75 torr, it converts into a liquid. At −40 °C, water goes from a gas to a solid as the pressure increases above very low values.
Q10.4.3
Pressure cookers allow food to cook faster because the higher pressure inside the pressure cooker increases the boiling temperature of water. A particular pressure cooker has a safety valve that is set to vent steam if the pressure exceeds 3.4 atm. What is the approximate maximum temperature that can be reached inside this pressure cooker? Explain your reasoning.
Q10.4.4
From the phase diagram for carbon dioxide, determine the state of CO2 at:
- 20 °C and 1000 kPa
- 10 °C and 2000 kPa
- 10 °C and 100 kPa
- −40 °C and 500 kPa
- −80 °C and 1500 kPa
- −80 °C and 10 kPa
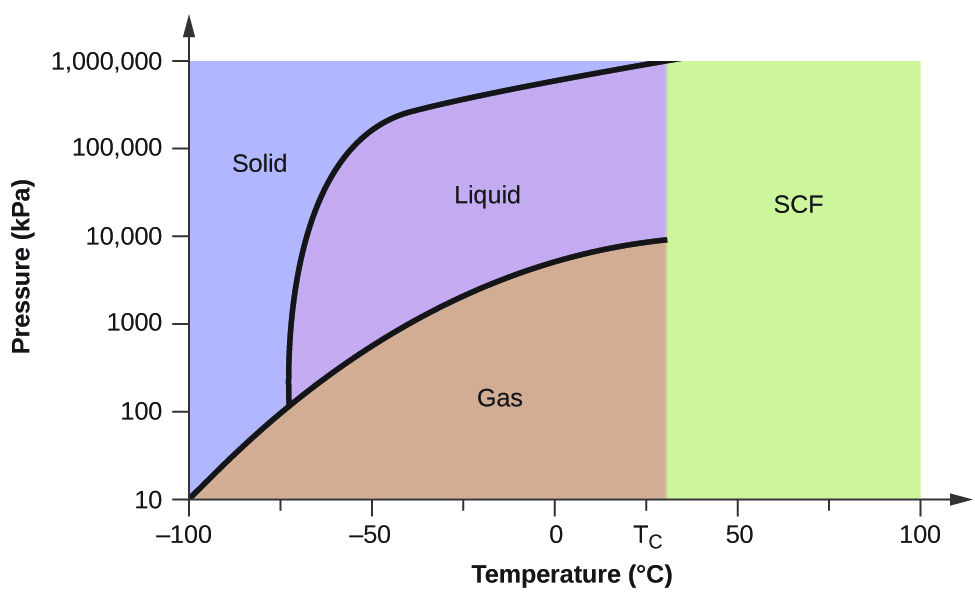
The pressure and temperature axes on this phase diagram of carbon dioxide are not drawn to constant scale in order to illustrate several important properties.
S10.4.4
(a) liquid; (b) solid; (c) gas; (d) gas; (e) gas; (f) gas
Q10.4.5
Determine the phase changes that carbon dioxide undergoes as the pressure changes if the temperature is held at −50 °C? If the temperature is held at −40 °C? At 20 °C?

The pressure and temperature axes on this phase diagram of carbon dioxide are not drawn to constant scale in order to illustrate several important properties.
Q10.4.6
Consider a cylinder containing a mixture of liquid carbon dioxide in equilibrium with gaseous carbon dioxide at an initial pressure of 65 atm and a temperature of 20 °C. Sketch a plot depicting the change in the cylinder pressure with time as gaseous carbon dioxide is released at constant temperature.
S10.4.6
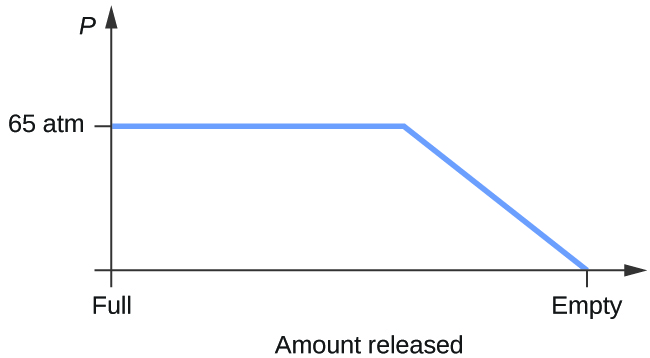
Q10.4.7
Dry ice, CO2(s), does not melt at atmospheric pressure. It sublimes at a temperature of −78 °C. What is the lowest pressure at which CO2(s) will melt to give CO2(l)? At approximately what temperature will this occur? (See Figure for the phase diagram.)
S10.4.7
Dry ice, CO2(s), will melt to give CO2(l) at 5.11 atm at −56.6 °C, the triple point of carbon dioxide.
Q10.4.8
If a severe storm results in the loss of electricity, it may be necessary to use a clothesline to dry laundry. In many parts of the country in the dead of winter, the clothes will quickly freeze when they are hung on the line. If it does not snow, will they dry anyway? Explain your answer.
S10.4.8
Yes, ice will sublime, although it may take it several days. Ice has a small vapor pressure, and some ice molecules form gas and escape from the ice crystals. As time passes, more and more solid converts to gas until eventually the clothes are dry.
Q10.4.9
Is it possible to liquefy nitrogen at room temperature (about 25 °C)? Is it possible to liquefy sulfur dioxide at room temperature? Explain your answers.
Q10.4.10
Elemental carbon has one gas phase, one liquid phase, and three different solid phases, as shown in the phase diagram:
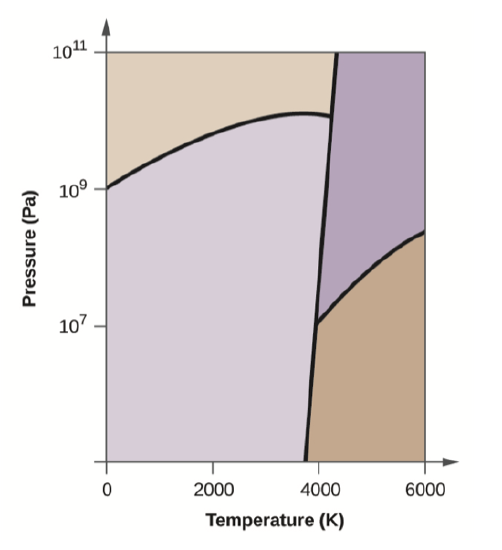
- On the phase diagram, label the gas and liquid regions.
- Graphite is the most stable phase of carbon at normal conditions. On the phase diagram, label the graphite phase.
- If graphite at normal conditions is heated to 2500 K while the pressure is increased to 1010 Pa, it is converted into diamond. Label the diamond phase.
- Circle each triple point on the phase diagram.
- In what phase does carbon exist at 5000 K and 108 Pa?
- If the temperature of a sample of carbon increases from 3000 K to 5000 K at a constant pressure of 106 Pa, which phase transition occurs, if any?
10.5: The Solid State of Matter
Q10.5.1
What types of liquids typically form amorphous solids?
S10.5.1
Amorphous solids lack an ordered internal structure. Liquid materials that contain large, cumbersome molecules that cannot move readily into ordered positions generally form such solids.
Q10.5.2
At very low temperatures oxygen, O2, freezes and forms a crystalline solid. Which best describes these crystals?
- ionic
- covalent network
- metallic
- amorphous
- molecular crystals
S10.5.3
(e) molecular crystals
Q10.5.4
As it cools, olive oil slowly solidifies and forms a solid over a range of temperatures. Which best describes the solid?
- ionic
- covalent network
- metallic
- amorphous
- molecular crystals
S10.5.4
(d) amorphous
Q10.5.5
Explain why ice, which is a crystalline solid, has a melting temperature of 0 °C, whereas butter, which is an amorphous solid, softens over a range of temperatures.
S10.5.6
Ice has a crystalline structure stabilized by hydrogen bonding. These intermolecular forces are of comparable strength and thus require the same amount of energy to overcome. As a result, ice melts at a single temperature and not over a range of temperatures. The various, very large molecules that compose butter experience varied van der Waals attractions of various strengths that are overcome at various temperatures, and so the melting process occurs over a wide temperature range.
Q10.5.7
Identify the type of crystalline solid (metallic, network covalent, ionic, or molecular) formed by each of the following substances:
- SiO2
- KCl
- Cu
- CO2
- C (diamond)
- BaSO4
- NH3
- NH4F
- C2H5OH
S10.5.7
(a) SiO2, covalent network; (b) KCl, ionic; (c) Cu, metallic; (d) CO, molecular; (e) C (diamond), covalent network; (f) BaSO4, ionic; (g) NH3, molecular; (h) NH4F, ionic; (i) C2H5OH, molecular
Q10.5.8
Identify the type of crystalline solid (metallic, network covalent, ionic, or molecular) formed by each of the following substances:
- CaCl2
- SiC
- N2
- Fe
- C (graphite)
- CH3CH2CH2CH3
- HCl
- NH4NO3
- K3PO4
S10.5.8
(a) CaCl2, ionic; (b) SiC, covalent network; (c) N2, molecular; (d) Fe, metallic; (e) C (graphite), covalent network; (f) CH3CH2CH2CH3, molecular; (g) HCl, molecular; (h) NH4NO3, ionic; (i) K3PO4, ionic
Q10.5.9
Classify each substance in the table as either a metallic, ionic, molecular, or covalent network solid:
| Substance | Appearance | Melting Point | Electrical Conductivity | Solubility in Water |
|---|---|---|---|---|
| X | lustrous, malleable | 1500 °C | high | insoluble |
| Y | soft, yellow | 113 °C | none | insoluble |
| Z | hard, white | 800 °C | only if melted/dissolved | soluble |
S10.5.9
X = metallic; Y = covalent network; Z = ionic
Q10.5.10
Classify each substance in the table as either a metallic, ionic, molecular, or covalent network solid:
| Substance | Appearance | Melting Point | Electrical Conductivity | Solubility in Water |
|---|---|---|---|---|
| X | brittle, white | 800 °C | only if melted/dissolved | soluble |
| Y | shiny, malleable | 1100 °C | high | insoluble |
| Z | hard, colorless | 3550 °C | none | insoluble |
S10.5.10
X = ionic; Y = metallic; Z = covalent network
Q10.5.11
Identify the following substances as ionic, metallic, covalent network, or molecular solids:
Substance A is malleable, ductile, conducts electricity well, and has a melting point of 1135 °C. Substance B is brittle, does not conduct electricity as a solid but does when molten, and has a melting point of 2072 °C. Substance C is very hard, does not conduct electricity, and has a melting point of 3440 °C. Substance D is soft, does not conduct electricity, and has a melting point of 185 °C.
S10.5.11
A = metallic; B = ionic; C = covalent network; D = molecular
Q10.5.12
Substance A is shiny, conducts electricity well, and melts at 975 °C. Substance A is likely a(n):
- ionic solid
- metallic solid
- molecular solid
- covalent network solid
S10.5.12
(b) metallic solid
Q10.5.13
Substance B is hard, does not conduct electricity, and melts at 1200 °C. Substance B is likely a(n):
- ionic solid
- metallic solid
- molecular solid
- covalent network solid
S10.5.13
(d) covalent network solid
10.6: Lattice Structures
Q10.6.1
Describe the crystal structure of iron, which crystallizes with two equivalent metal atoms in a cubic unit cell.
S10.6.1
The structure of this low-temperature form of iron (below 910 °C) is body-centered cubic. There is one-eighth atom at each of the eight corners of the cube and one atom in the center of the cube.
Q10.6.2
Describe the crystal structure of Pt, which crystallizes with four equivalent metal atoms in a cubic unit cell.
Q10.6.3
What is the coordination number of a chromium atom in the body-centered cubic structure of chromium?
S10.6.3
eight
Q10.6.4
What is the coordination number of an aluminum atom in the face-centered cubic structure of aluminum?
Q10.6.5
Cobalt metal crystallizes in a hexagonal closest packed structure. What is the coordination number of a cobalt atom?
S10.6.5
12
Q10.6.6
Nickel metal crystallizes in a cubic closest packed structure. What is the coordination number of a nickel atom?
Q10.6.7
Tungsten crystallizes in a body-centered cubic unit cell with an edge length of 3.165 Å.
- What is the atomic radius of tungsten in this structure?
- Calculate the density of tungsten.
S10.6.7
(a) 1.370 Å; (b) 19.26 g/cm
Q10.6.8
Platinum (atomic radius = 1.38 Å) crystallizes in a cubic closely packed structure. Calculate the edge length of the face-centered cubic unit cell and the density of platinum.
Q10.6.9
Barium crystallizes in a body-centered cubic unit cell with an edge length of 5.025 Å
- What is the atomic radius of barium in this structure?
- Calculate the density of barium.
S10.6.9
(a) 2.176 Å; (b) 3.595 g/cm3
Q10.6.10
Aluminum (atomic radius = 1.43 Å) crystallizes in a cubic closely packed structure. Calculate the edge length of the face-centered cubic unit cell and the density of aluminum.
Q10.6.11
The density of aluminum is 2.7 g/cm3; that of silicon is 2.3 g/cm3. Explain why Si has the lower density even though it has heavier atoms.
S10.6.11
The crystal structure of Si shows that it is less tightly packed (coordination number 4) in the solid than Al (coordination number 12).
Q10.6.12
The free space in a metal may be found by subtracting the volume of the atoms in a unit cell from the volume of the cell. Calculate the percentage of free space in each of the three cubic lattices if all atoms in each are of equal size and touch their nearest neighbors. Which of these structures represents the most efficient packing? That is, which packs with the least amount of unused space?
Q10.6.13
Cadmium sulfide, sometimes used as a yellow pigment by artists, crystallizes with cadmium, occupying one-half of the tetrahedral holes in a closest packed array of sulfide ions. What is the formula of cadmium sulfide? Explain your answer.
S10.6.13
In a closest-packed array, two tetrahedral holes exist for each anion. If only half the tetrahedral holes are occupied, the numbers of anions and cations are equal. The formula for cadmium sulfide is CdS.
Q10.6.14
A compound of cadmium, tin, and phosphorus is used in the fabrication of some semiconductors. It crystallizes with cadmium occupying one-fourth of the tetrahedral holes and tin occupying one-fourth of the tetrahedral holes in a closest packed array of phosphide ions. What is the formula of the compound? Explain your answer.
Q10.6.15
What is the formula of the magnetic oxide of cobalt, used in recording tapes, that crystallizes with cobalt atoms occupying one-eighth of the tetrahedral holes and one-half of the octahedral holes in a closely packed array of oxide ions?
S10.6.15
Co3O4
Q10.6.16
A compound containing zinc, aluminum, and sulfur crystallizes with a closest-packed array of sulfide ions. Zinc ions are found in one-eighth of the tetrahedral holes and aluminum ions in one-half of the octahedral holes. What is the empirical formula of the compound?
Q10.6.17
A compound of thallium and iodine crystallizes in a simple cubic array of iodide ions with thallium ions in all of the cubic holes. What is the formula of this iodide? Explain your answer.
S10.6.17
In a simple cubic array, only one cubic hole can be occupied be a cation for each anion in the array. The ratio of thallium to iodide must be 1:1; therefore, the formula for thallium is TlI.
Q10.6.18
Which of the following elements reacts with sulfur to form a solid in which the sulfur atoms form a closest-packed array with all of the octahedral holes occupied: Li, Na, Be, Ca, or Al?
Q10.6.19
What is the percent by mass of titanium in rutile, a mineral that contains titanium and oxygen, if structure can be described as a closest packed array of oxide ions with titanium ions in one-half of the octahedral holes? What is the oxidation number of titanium?
S10.6.19
59.95%; The oxidation number of titanium is +4.
Q10.6.20
Explain why the chemically similar alkali metal chlorides NaCl and CsCl have different structures, whereas the chemically different NaCl and MnS have the same structure.
Q10.6.21
As minerals were formed from the molten magma, different ions occupied the same cites in the crystals. Lithium often occurs along with magnesium in minerals despite the difference in the charge on their ions. Suggest an explanation.
S10.6.21
Both ions are close in size: Mg, 0.65; Li, 0.60. This similarity allows the two to interchange rather easily. The difference in charge is generally compensated by the switch of Si4+ for Al3+.
Q10.6.22
Rubidium iodide crystallizes with a cubic unit cell that contains iodide ions at the corners and a rubidium ion in the center. What is the formula of the compound?
Q10.6.23
One of the various manganese oxides crystallizes with a cubic unit cell that contains manganese ions at the corners and in the center. Oxide ions are located at the center of each edge of the unit cell. What is the formula of the compound?
S10.6.23
Mn2O3
Q10.6.24
NaH crystallizes with the same crystal structure as NaCl. The edge length of the cubic unit cell of NaH is 4.880 Å.
- Calculate the ionic radius of H−. (The ionic radius of Li+ is 0.0.95 Å.)
- Calculate the density of NaH.
Q10.6.25
Thallium(I) iodide crystallizes with the same structure as CsCl. The edge length of the unit cell of TlI is 4.20 Å. Calculate the ionic radius of TI+. (The ionic radius of I− is 2.16 Å.)
S10.6.25
1.48 Å
Q10.6.26
A cubic unit cell contains manganese ions at the corners and fluoride ions at the center of each edge.
- What is the empirical formula of this compound? Explain your answer.
- What is the coordination number of the Mn3+ ion?
- Calculate the edge length of the unit cell if the radius of a Mn3+ ion is 0.65 A.
- Calculate the density of the compound.
Q10.6.27
What is the spacing between crystal planes that diffract X-rays with a wavelength of 1.541 nm at an angle θ of 15.55° (first order reflection)?
S10.6.27
2.874 Å
Q10.6.28
A diffractometer using X-rays with a wavelength of 0.2287 nm produced first-order diffraction peak for a crystal angle θ = 16.21°. Determine the spacing between the diffracting planes in this crystal.
Q10.6.29
A metal with spacing between planes equal to 0.4164 nm diffracts X-rays with a wavelength of 0.2879 nm. What is the diffraction angle for the first order diffraction peak?
S10.6.29
20.2°
Q10.6.30
Gold crystallizes in a face-centered cubic unit cell. The second-order reflection (n = 2) of X-rays for the planes that make up the tops and bottoms of the unit cells is at θ = 22.20°. The wavelength of the X-rays is 1.54 Å. What is the density of metallic gold?
Q10.6.31
When an electron in an excited molybdenum atom falls from the L to the K shell, an X-ray is emitted. These X-rays are diffracted at an angle of 7.75° by planes with a separation of 2.64 Å. What is the difference in energy between the K shell and the L shell in molybdenum assuming a first-order diffraction?
S10.6.31
1.74 × 104 eV


