1.4: Measurements
- Page ID
- 221130
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)↵
- Explain the process of measurement and describe the three basic parts of a quantity.
- Describe the properties and units of length, mass, volume, density, temperature, and time.
- Recognize the common unit prefixes and use them to describe the magnitude of a measurement.
- Describe and calculate the density of a substance.
- Perform basic unit calculations and conversions in the metric and other unit systems.
Measurements provide the macroscopic information that is the basis of most of the hypotheses, theories, and laws that describe the behavior of matter and energy in both the macroscopic and microscopic domains of chemistry. Every measurement provides three kinds of information: the size or magnitude of the measurement (a number); a standard of comparison for the measurement (a unit); and an indication of the uncertainty of the measurement. While the number and unit are explicitly represented when a quantity is written, the uncertainty is an aspect of the measurement result that is more implicitly represented and will be discussed later.
The number in the measurement can be represented in different ways, including decimal form and scientific notation. For example, the maximum takeoff weight of a Boeing 777-200ER airliner is 298,000 kilograms, which can also be written as 2.98 \(\times\) 105 kg. The mass of the average mosquito is about 0.0000025 kilograms, which can be written as 2.5 \(\times\) 10−6 kg.
Units, such as liters, pounds, and centimeters, are standards of comparison for measurements. When we buy a 2-liter bottle of a soft drink, we expect that the volume of the drink was measured, so it is two times larger than the volume that everyone agrees to be 1 liter. The meat used to prepare a 0.25-pound hamburger is measured so it weighs one-fourth as much as 1 pound. Without units, a number can be meaningless, confusing, or possibly life threatening. Suppose a doctor prescribes phenobarbital to control a patient’s seizures and states a dosage of “100” without specifying units. Not only will this be confusing to the medical professional giving the dose, but the consequences can be dire: 100 mg given three times per day can be effective as an anticonvulsant, but a single dose of 100 g is more than 10 times the lethal amount.
We usually report the results of scientific measurements in SI units, an updated version of the metric system, using the units listed in Table \(\PageIndex{1}\). Other units can be derived from these base units. The standards for these units are fixed by international agreement, and they are called the International System of Units or SI Units (from the French, Le Système International d’Unités). SI units have been used by the United States National Institute of Standards and Technology (NIST) since 1964.
| Property Measured | Name of Unit | Symbol of Unit |
|---|---|---|
| length | meter | m |
| mass | kilogram | kg |
| time | second | s |
| temperature | kelvin | K |
| electric current | ampere | A |
| amount of substance | mole | mol |
| luminous intensity | candela | cd |
Sometimes we use units that are fractions or multiples of a base unit. Ice cream is sold in quarts (a familiar, non-SI base unit), pints (0.5 quart), or gallons (4 quarts). We also use fractions or multiples of units in the SI system, but these fractions or multiples are always powers of 10. Fractional or multiple SI units are named using a prefix and the name of the base unit. For example, a length of 1000 meters is also called a kilometer because the prefix kilo means “one thousand,” which in scientific notation is 103 (1 kilometer = 1000 m = 103 m). The prefixes used and the powers to which 10 are raised are listed in Table \(\PageIndex{2}\).
NG, equals 4 times ten to the negative 9, or 0.000000004 g. The prefix micro has the greek letter mu as its symbol and a factor of 10 to the negative sixth power. Therefore, 1 microliter, or mu L, is equal to one times ten to the negative 6 or 0.000001 L. The prefix milli has a lowercase M as its symbol and a factor of 10 to the negative third power. Therefore, 2 millimoles, or M mol, are equal to two times ten to the negative 3 or 0.002 mol. The prefix centi has a lowercase C as its symbol and a factor of 10 to the negative second power. Therefore, 7 centimeters, or C M, are equal to seven times ten to the negative 2 meters or 0.07 M O L. The prefix deci has a lowercase D as its symbol and a factor of 10 to the negative first power. Therefore, 1 deciliter, or lowercase D uppercase L, are equal to one times ten to the negative 1 meters or 0.1 L. The prefix kilo has a lowercase K as its symbol and a factor of 10 to the third power. Therefore, 1 kilometer, or K M, is equal to one times ten to the third meters or 1000 M. The prefix mega has an uppercase M as its symbol and a factor of 10 to the sixth power. Therefore, 3 megahertz, or M H Z, are equal to three times 10 to the sixth hertz, or 3000000 H Z. The prefix giga has an uppercase G as its symbol and a factor of 10 to the ninth power. Therefore, 8 gigayears, or G Y R, are equal to eight times 10 to the ninth years, or 800000000 G Y R. The prefix tera has an uppercase T as its symbol and a factor of 10 to the twelfth power. Therefore, 5 terawatts, or T W, are equal to five times 10 to the twelfth watts, or 5000000000000 W." data-quail-id="64" data-mt-width="1076">
| Prefix | Symbol | Factor | Example |
|---|---|---|---|
| femto | f | 10−15 | 1 femtosecond (fs) = 1 \(\times\) 10−15 s (0.000000000000001 s) |
| pico | p | 10−12 | 1 picometer (pm) = 1 \(\times\) 10−12 m (0.000000000001 m) |
| nano | n | 10−9 | 4 nanograms (ng) = 4 \(\times\) 10−9 g (0.000000004 g) |
| micro | µ | 10−6 | 1 microliter (μL) = 1 \(\times\) 10−6 L (0.000001 L) |
| milli | m | 10−3 | 2 millimoles (mmol) = 2 \(\times\) 10−3 mol (0.002 mol) |
| centi | c | 10−2 | 7 centimeters (cm) = 7 \(\times\) 10−2 m (0.07 m) |
| deci | d | 10−1 | 1 deciliter (dL) = 1 \(\times\) 10−1 L (0.1 L ) |
| kilo | k | 103 | 1 kilometer (km) = 1 \(\times\) 103 m (1000 m) |
| mega | M | 106 | 3 megahertz (MHz) = 3 \(\times\) 106 Hz (3,000,000 Hz) |
| giga | G | 109 | 8 gigayears (Gyr) = 8 \(\times\) 109 yr (8,000,000,000 Gyr) |
| tera | T | 1012 | 5 terawatts (TW) = 5 \(\times\) 1012 W (5,000,000,000,000 W) |
SI Base Units
The initial units of the metric system, which eventually evolved into the SI system, were established in France during the French Revolution. The original standards for the meter and the kilogram were adopted there in 1799 and eventually by other countries. This section introduces four of the SI base units commonly used in chemistry. Other SI units will be introduced in subsequent chapters.
Length
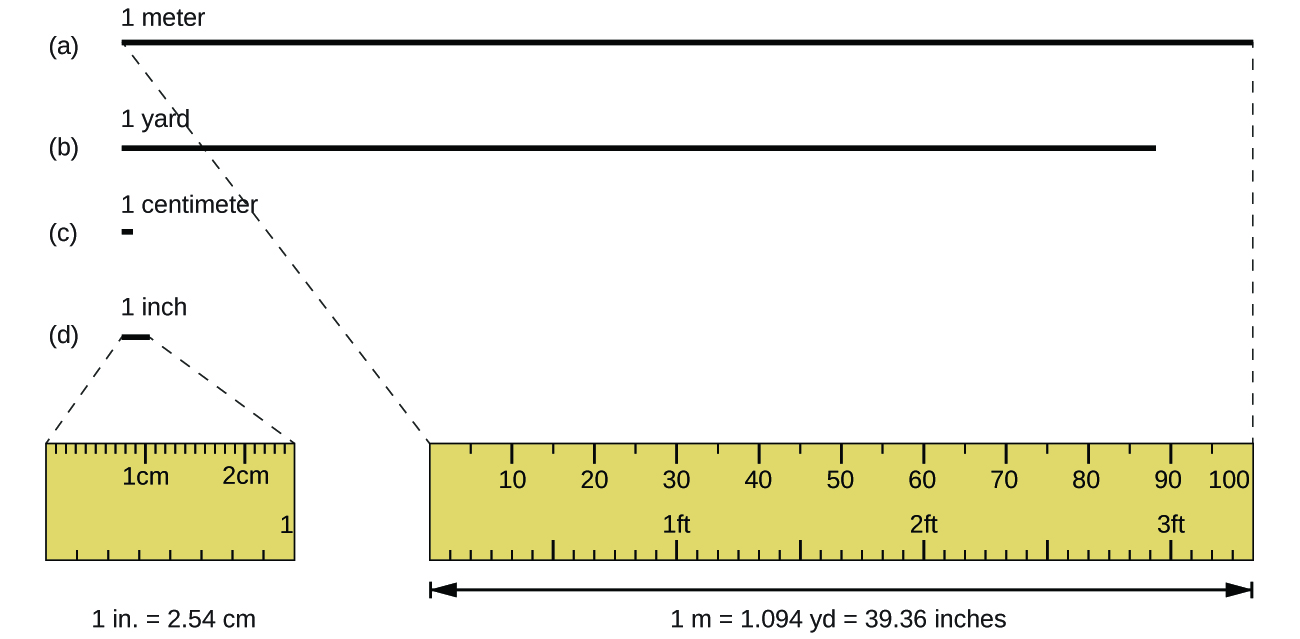
The standard unit of length in both the SI and original metric systems is the meter (m). A meter was originally specified as 1/10,000,000 of the distance from the North Pole to the equator. It is now defined as the distance light in a vacuum travels in 1/299,792,458 of a second. A meter is about 3 inches longer than a yard (Figure \(\PageIndex{1}\)); one meter is about 39.37 inches or 1.094 yards. Longer distances are often reported in kilometers (1 km = 1000 m = 103 m), whereas shorter distances can be reported in centimeters (1 cm = 0.01 m = 10−2 m) or millimeters (1 mm = 0.001 m = 10−3 m).
Mass
The standard unit of mass in the SI system is the kilogram (kg). A kilogram was originally defined as the mass of a liter of water (a cube of water with an edge length of exactly 0.1 meter). It is now defined by a certain cylinder of platinum-iridium alloy, which is kept in France (Figure 1.4.2). Any object with the same mass as this cylinder is said to have a mass of 1 kilogram. One kilogram is about 2.2 pounds. The gram (g) is exactly equal to 1/1000 of the mass of the kilogram (10−3 kg).

Temperature
Temperature is an intensive property. The SI unit of temperature is the kelvin (K). The IUPAC convention is to use kelvin (all lowercase) for the word, K (uppercase) for the unit symbol, and neither the word “degree” nor the degree symbol (°). The degree Celsius (°C) is also allowed in the SI system, with both the word “degree” and the degree symbol used for Celsius measurements. Celsius degrees are the same magnitude as those of kelvin, but the two scales place their zeros in different places. Water freezes at 273.15 K (0 °C) and boils at 373.15 K (100 °C) by definition, and normal human body temperature is approximately 310 K (37 °C). The conversion between these two units and the Fahrenheit scale will be discussed later in this chapter.
Time
The SI base unit of time is the second (s). Small and large time intervals can be expressed with the appropriate prefixes; for example, 3 microseconds = 0.000003 s = 3 \(\times\) 10−6 and 5 megaseconds = 5,000,000 s = 5 \(\times\) 106 s. Alternatively, hours, days, and years can be used.
Derived SI Units
We can derive many units from the seven SI base units. For example, we can use the base unit of length to define a unit of volume, and the base units of mass and length to define a unit of density.
Volume
Volume is the measure of the amount of space occupied by an object. The standard SI unit of volume is defined by the base unit of length (Figure \(\PageIndex{3}\)). The standard volume is a cubic meter (m3), a cube with an edge length of exactly one meter. To dispense a cubic meter of water, we could build a cubic box with edge lengths of exactly one meter. This box would hold a cubic meter of water or any other substance.
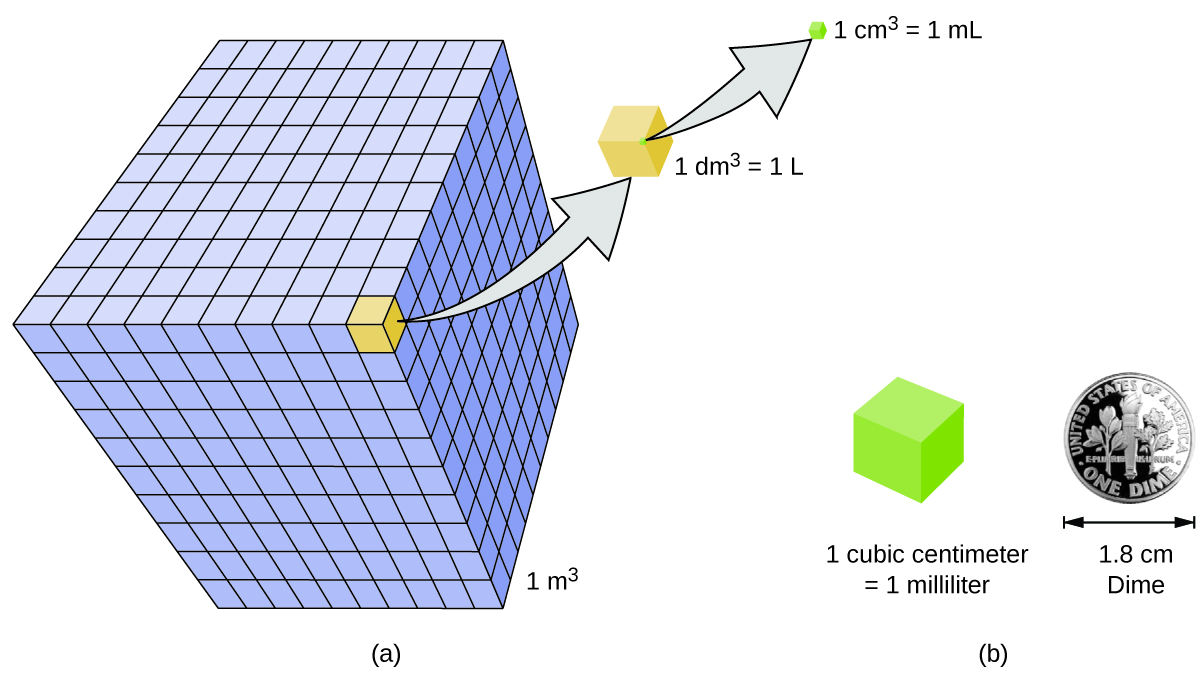
A more commonly used unit of volume is derived from the decimeter (0.1 m, or 10 cm). A cube with edge lengths of exactly one decimeter contains a volume of one cubic decimeter (dm3). A liter (L) is the more common name for the cubic decimeter. One liter is about 1.06 quarts. A cubic centimeter (cm3) is the volume of a cube with an edge length of exactly one centimeter. The abbreviation cc (for cubic centimeter) is often used by health professionals. A cubic centimeter is also called a milliliter (mL) and is 1/1000 of a liter.
Density
We use the mass and volume of a substance to determine its density. Thus, the units of density are defined by the base units of mass and length.
The density of a substance is the ratio of the mass of a sample of the substance to its volume. The SI unit for density is the kilogram per cubic meter (kg/m3). For many situations, however, this as an inconvenient unit, and we often use grams per cubic centimeter (g/cm3) for the densities of solids and liquids, and grams per liter (g/L) for gases. Although there are exceptions, most liquids and solids have densities that range from about 0.7 g/cm3 (the density of gasoline) to 19 g/cm3 (the density of gold). The density of air is about 1.2 g/L. Table \(\PageIndex{3}\) shows the densities of some common substances.
| Solids | Liquids | Gases (at 25 °C and 1 atm) |
|---|---|---|
| ice (at 0 °C) 0.92 g/cm3 | water 1.0 g/cm3 | dry air 1.20 g/L |
| oak (wood) 0.60–0.90 g/cm3 | ethanol 0.79 g/cm3 | oxygen 1.31 g/L |
| iron 7.9 g/cm3 | acetone 0.79 g/cm3 | nitrogen 1.14 g/L |
| copper 9.0 g/cm3 | glycerin 1.26 g/cm3 | carbon dioxide 1.80 g/L |
| lead 11.3 g/cm3 | olive oil 0.92 g/cm3 | helium 0.16 g/L |
| silver 10.5 g/cm3 | gasoline 0.70–0.77 g/cm3 | neon 0.83 g/L |
| gold 19.3 g/cm3 | mercury 13.6 g/cm3 | radon 9.1 g/L |
While there are many ways to determine the density of an object, perhaps the most straightforward method involves separately finding the mass and volume of the object, and then dividing the mass of the sample by its volume. In the following example, the mass is found directly by weighing, but the volume is found indirectly through length measurements.
\[\mathrm{density=\dfrac{mass}{volume}} \nonumber \]
Calculation of Density Gold—in bricks, bars, and coins—has been a form of currency for centuries. In order to swindle people into paying for a brick of gold without actually investing in a brick of gold, people have considered filling the centers of hollow gold bricks with lead to fool buyers into thinking that the entire brick is gold. It does not work: Lead is a dense substance, but its density is not as great as that of gold, 19.3 g/cm3. What is the density of lead if a cube of lead has an edge length of 2.00 cm and a mass of 90.7 g?
Solution
The density of a substance can be calculated by dividing its mass by its volume. The volume of a cube is calculated by cubing the edge length.
\[\mathrm{volume\: of\: lead\: cube=2.00\: cm\times2.00\: cm\times2.00\: cm=8.00\: cm^3} \nonumber \]
\[\mathrm{density=\dfrac{mass}{volume}=\dfrac{90.7\: g}{8.00\: cm^3}=\dfrac{11.3\: g}{1.00\: cm^3}=11.3\: g/cm^3} \nonumber \]
(We will discuss the reason for rounding to the first decimal place in the next section.)
- To three decimal places, what is the volume of a cube (cm3) with an edge length of 0.843 cm?
- If the cube in part (a) is copper and has a mass of 5.34 g, what is the density of copper to two decimal places?
- Answer a
-
0.599 cm3;
- Answer b
-
8.91 g/cm3
This PhET simulation illustrates another way to determine density, using displacement of water. Determine the density of the red and yellow blocks.
Solution
When you open the density simulation and select Same Mass, you can choose from several 5.00-kg colored blocks that you can drop into a tank containing 100.00 L water. The yellow block floats (it is less dense than water), and the water level rises to 105.00 L. While floating, the yellow block displaces 5.00 L water, an amount equal to the weight of the block. The red block sinks (it is more dense than water, which has density = 1.00 kg/L), and the water level rises to 101.25 L.
The red block therefore displaces 1.25 L water, an amount equal to the volume of the block. The density of the red block is:
\[\mathrm{density=\dfrac{mass}{volume}=\dfrac{5.00\: kg}{1.25\: L}=4.00\: kg/L} \nonumber \]
Note that since the yellow block is not completely submerged, you cannot determine its density from this information. But if you hold the yellow block on the bottom of the tank, the water level rises to 110.00 L, which means that it now displaces 10.00 L water, and its density can be found:
\[\mathrm{density=\dfrac{mass}{volume}=\dfrac{5.00\: kg}{10.00\: L}=0.500\: kg/L} \nonumber \]
Remove all of the blocks from the water and add the green block to the tank of water, placing it approximately in the middle of the tank. Determine the density of the green block.
- Answer
-
2.00 kg/L
Summary
Measurements provide quantitative information that is critical in studying and practicing chemistry. Each measurement has an amount, a unit for comparison, and an uncertainty. Measurements can be represented in either decimal or scientific notation. Scientists primarily use the SI (International System) or metric systems. We use base SI units such as meters, seconds, and kilograms, as well as derived units, such as liters (for volume) and g/cm3 (for density). In many cases, we find it convenient to use unit prefixes that yield fractional and multiple units, such as microseconds (10−6 seconds) and megahertz (106 hertz), respectively.
Key Equations
- \(\mathrm{density=\dfrac{mass}{volume}}\)
Glossary
- Celsius (°C)
- unit of temperature; water freezes at 0 °C and boils at 100 °C on this scale
- cubic centimeter (cm3 or cc)
- volume of a cube with an edge length of exactly 1 cm
- cubic meter (m3)
- SI unit of volume
- density
- ratio of mass to volume for a substance or object
- kelvin (K)
- SI unit of temperature; 273.15 K = 0 ºC
- kilogram (kg)
- standard SI unit of mass; 1 kg = approximately 2.2 pounds
- length
- measure of one dimension of an object
- liter (L)
- (also, cubic decimeter) unit of volume; 1 L = 1,000 cm3
- meter (m)
- standard metric and SI unit of length; 1 m = approximately 1.094 yards
- milliliter (mL)
- 1/1,000 of a liter; equal to 1 cm3
- second (s)
- SI unit of time
- SI units (International System of Units)
- standards fixed by international agreement in the International System of Units (Le Système International d’Unités)
- unit
- standard of comparison for measurements
- volume
- amount of space occupied by an object


