5.01: Equilibrium & The Steady State Condition

Figure 5-2. The amount of water in this natural pool is determined by the balanced of two opposing processes: the rate of flow into the pool from the waterfall, and the rate of flow out of the pool by a stream. When these two rates are the same the level of water is steady, but if either of them exceeds the other the water level will rise or fall until a new balance is achieved at a different water level. "Buffalo River Waterfall" by Buffalo Outdoor Center is licensed under CC BY-ND 2.0.

 

We'll begin our discussion of equilibrium with a few physical systems in which there is nothing really "chemical" going on. Why? Because the ideas of equilibrium are quite general and a deeper conceptual understanding of the concept in chemistry is easier to develop if you have a more fundamental understanding of the phenomemon. Consider, for example, the pool of water shown in Figure 5-2, or more specifically the amount of water in it. Imagine yourself serenely observing the pool over a few hours. Despite the fact that water is continuously flowing into the pool, the water level doesn't change. Why? Simple: water is also flowing out. The two processes essentially cancel each other out: the amount of water flowing in equals the amount of water flowing out, so the water level stays the same. The amount of water in the pool is said to be at steady state, meaning that, despite the fact that water is simultaneously flowing into and out of the pool, there is no net change in the amount of water in it.

We can model a similar system mathematically. Models of physical or chemical systems are useful because they allow you to predict how particular changes in the system might affect the state of the system at steady state, or how much time might be requires for a system to re-establish equilibrium after a disturbance. For example, in the above example, we might think about how high the water might rise in the pool if the influx was to increase, because of a recent rain for example. Or, how the level might rise if a beaver were to partially block the outflow by building a dam. The accuracy of the model depends on how well the various characteristics of the actual physical system are taken into account. Thus, for a very irregularly shaped pool, with irregularly shaped channels leading into and out of it, developing an accurate model might be difficult, or at least time-consuming. For our purposes, we'll consider a very simple physical system: a small sink into which water is flowing at a constant rate (Figure 5-3a). The exit drain is small enough where the water flowing into the drain can't immediately flow out. Instead, water gradually accumulates in the sink as it flows in. You may have encountered this if a drain in a kitchen or bathroom sink is partially clogged. It may not be obvious at first, but the rate of flow out the drain will not be constant, but will increase as the amount of water in the sink increases. This is because as the depth of the water in the sink increases, the rate it flows through the drain also increases; in effect, the additional weight of the water above the drain forces water to flow through the opening faster. The rate of water going into and out of the sink are shown in the graph at right (Figure 5-3b); notice that we keep the flow from the tap (shown in red) to be a constant 100 mL/sec, a typical value for a fully open tap. The flow out of the drain, which is calculated based on Torricelli's Law, starts very low but increases rapidly. The outflow continues to increase as the water in the sink gets deeper and approaches that of the water being added. As the difference between the two rates gets smaller, the amount of water flowing out through the drain gets closer and closer to the amount being added. The rate of outflow asymptotically approaches the inflow rate. Given the specific parameters used in this model, the two flow rates are within 0.1% of each other at after about 80 seconds, meaning that the system is approaching steady state. Figure 5-3c shows the depth of water as a function of time and also illustrates the system approaching steady steady as the depth reaches a plateau. If the rate of water being added does not change, the depth will remain at that steady state value indefinitely. The parallels between this example and the natural pool shown in Figure 5-2 should be clear.

 

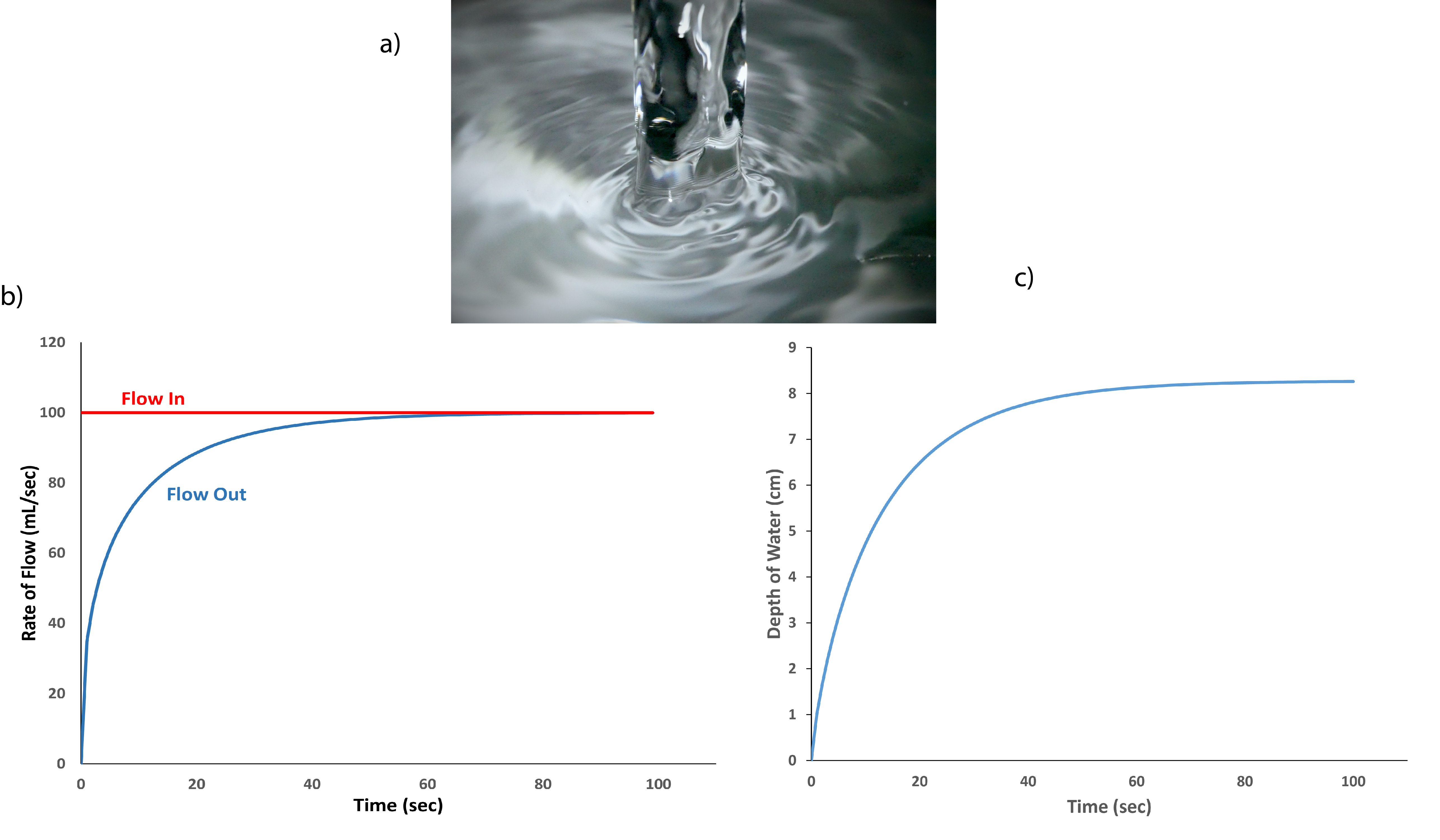
Figure 5-3. (a) water being added to a small sink. In the mathematical model discussed in the text, there is a small drain at the bottom of the sink so water is flowing out as it is being added. (b) The rate of inflow and outflow used in the model; inflow is kept at a constant value of 100 mL/sec, while the rate of outflow increases as water accumulates in the sink. (c) The depth of water in the sink as a function of time; as it gets deeper it causes the rate of outflow to increase until the outflow becomes equal to the inflow. At that point the volume of water, and hence the depth of water, is said to be at steady state and will remain constant until either the inflow or outflow changes. 

 

Before moving on to other examples of equilibrium, it is worth examining a few other aspects of this condition. First, let's distinguish dynamic equilibrium from static systems. Imagine the tap was hidden from view, perhaps by being below the surface of the water, and the only observable feature using the rocks of the cave as a reference point for example, could we tell if there was water flowing into and out of the pool. No, the fact that the water level is at steady state makes it appear as if there might not be any flow of water at all. Such a system would not at equilibrium, at least in terms of the flow of water. It would be considered a static system, that is one, where there is no events taking place that might shift the property that you are observing. This is in contrast to dynamic systems where opposing events are taking place. When those opposing events balance each other, such systems are said to be in a state of dynamic equilibrium.

Examples of systems that are in dynamic equilibrium abound. Consider a tightrope walker, such as the child shown in Figure 5-3. Acrobats like these must balance the forces that would make them fall to the left or right of the cable upon which they are perched. This is analogous to the water flowing into and out of the pool: at the balance point, these forces are in equilibrium and the tightrope walker is in a position of steady state, although she also moves in a forward direction while maintaining the balance between her lateral positions. The fact that the tightrope walker does not fall does not mean that there are no forces acting on her; rather, it means that those forces that would pull her to one side or the other are balanced. 

 

Figure 5-3. This child is practicing tightrope walking. Her side-to-side balance is in a state of dynamic equilibrium because there are forces acting on her that would pull her down on the left and right. She maintains her balance by adjusting the pole such that the forces acting on her remain equal as she moves forward. (image credit: "Tightrope Walking" by jackol is licensed under CC BY-NC-SA 2.0.)

 

Another example that is particularly urgent from an environmental perspective: the energy budget for planet Earth. Despite the occasional ice age, the temperature of the earth's surface has remained remarkable stable over hundreds of millions of years: it is warm enough to have oceans of liquid water but cool enough to prevent that water from boiling away. But everyday the amount of solar energy reaching the Earth's surface is unfathomably large (greater than the amount of energy used by the entire world's population each year). If the surface of the earth had no way of releasing that energy back out into space, the surface would get increasingly warm and make the planet uninhabitable in a matter of days. So how does the energy leave? Through a process called radiational heating [1]. Every object radiates energy from its surface in the form of electromagnetic radiation. Your skin, for example, emits infrared radiation that is visible on night vision googles. The warmer the surface, the more energy is radiated outwards. This is demonstrated nicely by electric stove elements as they heat: at room temperature they emit no visible light, but as they warm they eventually emit a dull red light, brightening and shifting to the orange at their highest temperature. Incandescent light bulbs work by heating a filament to roughly 3,000 C, where they emit a warm, white light. The planet is no different: it radiates out into space roughly the same amount of energy it absorbs in the form of visible light from the sun. The mechanism of climate change involves a slight adjustment of that energy balance. Greenhouse gases, such as water vapor and carbon dioxide, impede the radiation from the surface, in effect trapping some heat in the atmosphere. The result is that the surface needs to be warmer that it otherwise would be to establish an energy balance. This is because the surface needs to be a bit warmer for the amount of radiation that escapes into space to balance the energy influx from the sun. As humans increase the concentration of greenhouse gases, especially carbon dioxide, the effect is enhanced causing a slight but significant increase in temperature.

The idea of equilibrium extends even into fields outside of the physical sciences. Biologists study homeostatic mechanisms by which organisms maintain body temperatures within a very narrow window, or how the concentration of glucose in the blood is kept within a certain range. Economists use the concept of equilibrium in the establishment of prices as the point at which there is "balance" between supply and demand.

Let's take a look at a system that starts in a condition where it is not at equilibrium but eventually reaches steady state. Consider a sink that is initially empty but into which we allow water to flow at a constant rate; there is drain at the bottom of the sink through which water can flow. This is very similar to the natural pool shown in Figure 5-2. We want to calculate the height of the water in the sink as water flows into and out of it over time.  

 

The equations depicted in Figure 5-2 are shown with pairs of oppositely directed arrows to indicate that the reactions can proceed in both directions. In other words, two molecules of water can react to form hydronium and hydroxide (autoionization), or hydronium and hydroxide can combine to make two molecules of water (neutralization). This is but one example of many such chemical and physical systems that are characterized by a balance of two processes that oppose each other. Such systems are said to be in dynamic equilibrium. This term means that there are opposing events that have no net effect on the system. This is contrast to static systems that undergo no change because there are no processes or forces at all acting on them. They may appear the similar – neither exhibit discernable changes over time – bt they are quite different. Everything from the energy budget that establishes the temperature of the Earth, to homeostatic processes that regulate your body temperature, to the level of water in a mountain pool are examples of systems in dynamic equilibrium. The water level of a pool (Figure 5-5), for example, is determined by the to rate of water flowing in compared to the rate of water flowing out. If the two rates are the same, the water level is stable. If the rate of water flowing into a natural pool, such as during a spring thaw when snow melts quickly, the level water level goes up. During times of drought, the rate of water flowing out of the lake exceed that flowing in and the level drops. That may seem intuitive, but what may not be obvious is that these rates caffect one another. If the level of the pool increases, the outflow will also increase because the added height of the water will likely widen the mouth of the stream. An increase inflow will cause the outflow to increase until the two become equal once again and a new equilibrium water level will be achieved and it will remain until either the inflow or outflow is disturbed again.  

The temperature of the Earth (or any other planet), is determined by the balance of energy flowing into the planet (from the sun) compared to energy radiating out from the surface. The temperature of the Earth rises or falls depending on how this balance is established. When the planet's ability to radiate energy out into space is inhibited (such as by the increase in greenhouse gases), the temperature increases until balance is restored (the warmer the surface of the planet, the more energy is radiated outward).

The above processes are purely physical but provide useful analogies to chemical equilibria such as the autoionization/neutralization reactions described in the previous section. Given those two opposing reactions one could ask that, at any given time, which direction predominates, autoionization or neutralization? And how could you tell? The water analogy may be useful here. Consider the amount of water in the pool to be analogous to the concentrations of H₃O⁺ and OH^-. The process that generates the ions is autoionization, which is analagous to the influx of water to the pool; water in the pool can be viewed as the "product" of the process. The neutralization reaction consumes the ions and is analogous to water flowing out of the pool because the process decreases the amount of "product". If the inflow exceeds the outflow, the amount of product – water in the pool – increases. Likewise, if the rate of autoionization exceeds that of neutralization, the concentrations of H₃O⁺ and OH^- will increase. Conversely, if the rate of neutralization exceeds autoionization, these concentrations will decrease.

We could therefore investigate the question by measuring the concentrations of hydronium and hydroxide ions over time. An increase in those concentrations would indicate that autoionization is taking place faster than neutralization. If, however, the concentrations of those ions decrease, then neutralization is the predominant pathway. If we were to make such a measurement in otherwise pure water, we would see that the concentration of these ions are equal: [H₃O⁺] = [OH^-] = 1.0x10^-7 M. Moreover, these concentrations do not change over time. The latter point is significant because it implies that the rate of their formation balances that of their consumption, that is, the rate of autoionization is exactly the same as the rate of neutralization so that no net change is observed. This is analagous to the water level in the pool staying the same over an extended period.

Let's pause here to consider a different interpretation of those results. Can it be that the lack of any change in those concentrations means that, while the reaction is capable of proceeding in both directions, there may in fact be no reaction taking place at all. Which is it? Is there a balance of two opposing reactions? Or is there no reaction taking place at all? In the case of the pool, it is a simple question: we can see that there is water going into and out of the pool, so there is no question that it is a case of dynamic equilibrium. But we can't see either the autoionization or neutralization reactions in a similar way, so what evidence is there that it is a case of dynamic equilibrium as opposed to simple stasis. Some clues to the answer can be found by neutralizing an acidic solution with a basic one. Acidic solutions are those that have more hydronium ions than hydroxide, while basic solutions have more hydroxide ions. Solutions that have an equal concentration of these ions are referred to as neutral. When mixed, the hydronium ions of an acidic solution will react with hydroxide ions of a basic one, neutralizing each other to form water as shown in Figure 5-4. But the reaction does not go to completion. If done carefully, meaning that the amount of base added exactly equals that of the acid present (on a mole to mole basis), most of these ions react to form water and the resulting solution will not have an excess of either one. Yet some of each will remain. The resulting concentrations of these ions will be, coincidentally enough, 1.0 × 10^-7 M – the same concentration observed in "pure" water. Clearly, neutralization will be the dominant reaction if the initial concentrations of hydronium and hydroxide are relatively high. The fact that the same concentrations are obtained in pure water implies that autoionization is the dominant reaction if the concentrations of hydronium and hydroxide are low (where low means less than 1.0 × 10^-7 M). But regardless of the initial condition, when the concentrations of these ions reach 1.0 × 10^-7 M, the reaction appears to stop, with no further changes in concentration taking place. We can infer, therefore, that these concentrations represent a sort of energetic minimum that can be approached from either conditions in which they are too low or too high. Moreover, the fact that the same concentrations of ions are reached from either direction is definitive proof that the steady state condition described above is due to a balance of opposing reaction rates – not a static condition in which no reaction is occurring – as we explain more fully below. 

There are many examples of chemical reactions that behave similarly to that just described. They proceed partially to completion before slowing down and appearing to stop. Hemoglobin is a case in point. This protein in your red blood cells loosely binds oxygen from your lungs and transports it to cells where, like cargo, it is dropped off to be used for aerobic respiration. But when exposed to air most, but not all, of the hemoglobin binds to O₂; some hemoglobin molecules are carried off with no oxygen cargo, arriving empty-handed at waiting cells. Likewise, when hemoglobin reaches cells, some portion of the oxygen stays attached to the protein and returns to the lungs unused, that is, with the oxygen cargo still on board. While this may seem like an inefficient transportation mechanism, it is an inevitable result of how systems behave when governed by equilibrium processes.

We’ll return to hemoglobin in a bit, but let’s examine chemical equilibrium with a much simpler example – the evaporation of water. Consider the following scenario: imagine introducing water into a completely evacuated chamber, that is, one that contains no air at all; we do not fill the chamber, but we add enough water such that when some of the liquid evaporates, there will be some liquid water remaining. The chemical equation that describes the vaporization of water is a simple one:

\[ \ce{H2O} (l) \ce{ ->   H2O} (g) \]

The evaporated water, being a gas, will exert a pressure on the walls of the container that could be monitored using a pressure sensor [5]. We can graph the gaseous pressure as a function of time. What would such a plot look like?  You know that initially the pressure begins at zero because it is a vacuum. Moreover, some of the water we add will evaporate almost instantly, resulting in a rapid increase in gas pressure on the inside walls of the chamber. And common sense tells you that at some point it should stop increasing – bottles of water would explode if the apparent rate of evaporation did not eventually stop. One possibility, therefore, would be an “angular” plot, with the pressure increasing steadily and then, at some point when the space above the liquid can hold no more gaseous water, evaporation stops. Such a scheme is implausible because there does not exist a mechanism by which the system “knows” when evaporation should cease. Compare this to the following.

A more realistic (and intuitive) plot of the pressure exerted by the gaseous water molecules as a function of time that we would expect from the above scenario is shown in Figure 5-5. Unlike the angular plot described above, the rate of increase in this case is large at first but smoothly and gradually decreases until a plateau is attained. It is important to note that the gradual slowing of the pressure rise is not due to the complete loss of liquid water; indeed, in our experimental design, we explicitly stated that there would be some liquid water present at all times. Moreover, the rate of evaporation stays more or less constant provided the surface area of the liquid does not change, which we’ll assume is true. In the absence of competing effects, a constant rate of evaporation should show a linear increase in the pressure of the water vapor as the angular plot described above would yield. But this is not seen experimentally. Rather, as we have described already in other contexts, the reaction appears to proceed only partially to completion and then seems to stop.

 

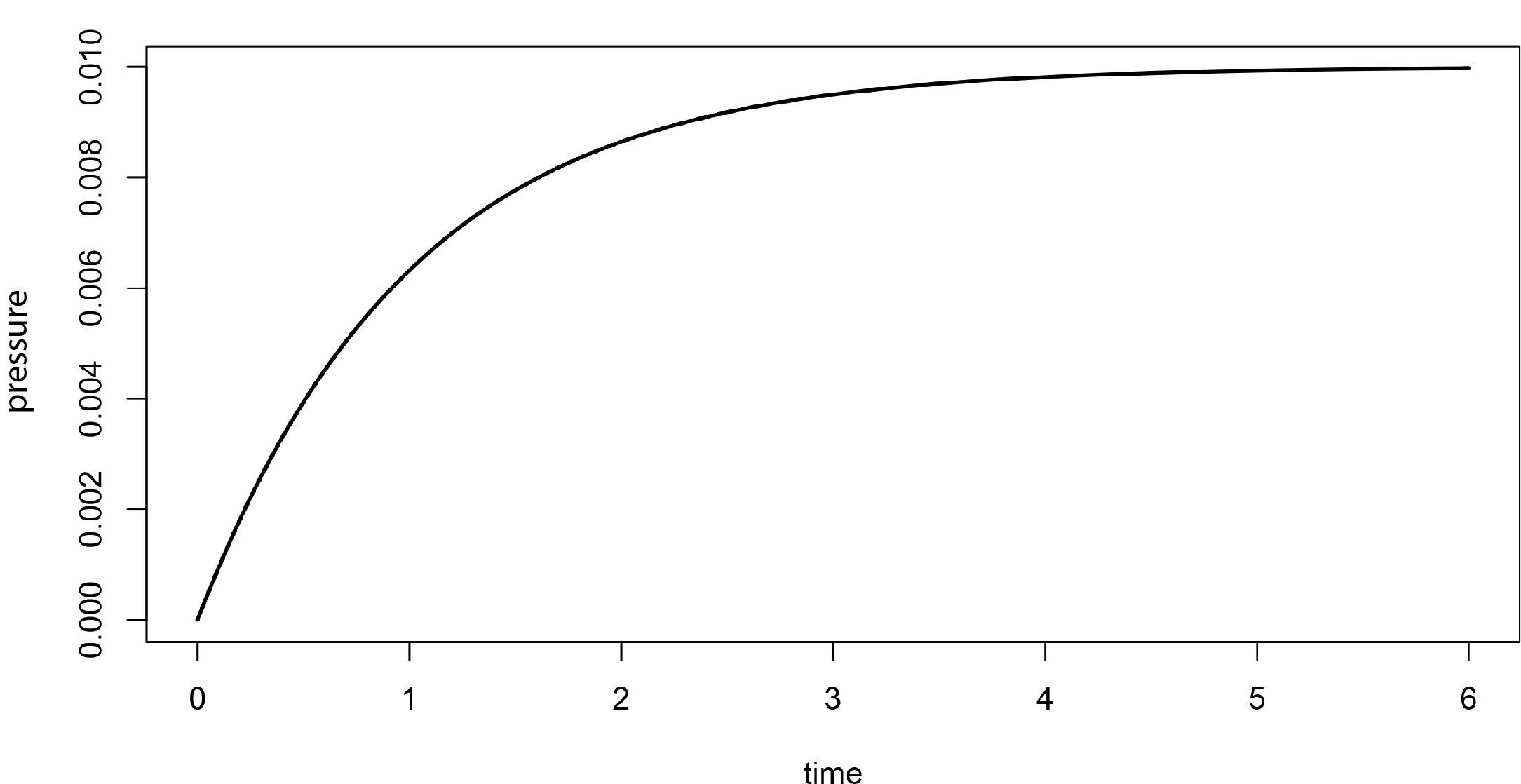
Figure 5-5. A plot of the pressure exerted by water vapor in the thought experiment outlined in the text. The shape of the curve is characteristic of those seen in systems with opposing processes that approach steady state; the rate of the reaction appears to slow down over time as the opposing reaction speeds up. When the reverse rate becomes equal to the forward rate, the system achieves steady state and no further net change will be seen until the equilibrium is disturbed in some way by an external event.

 

The only reasonable explanation for the gradual decrease in apparent reaction rate is that the opposing reaction, the condensation of water, speeds up over time. This should be intuitively pleasing: when there is no (or very little) water vapor in the chamber, there can be no condensation of gaseous water to the liquid state. At longer times, as the amount of gaseous water increases, the rate of condensation increases, eventually becoming equal to the evaporation rate. There is no net change in pressure after that point and the liquid and gaseous states of water are said to be in dynamic equilibrium. Therefore it would be incorrect to say that evaporation stops when the pressure stabilizes. Rather, it is in a condition of steady state, meaning that there are no net changes because the rate of the forward reaction (evaporation) is balanced by that of the reverse (condensation). We see, therefore, that the chemical equation above would therefore be more usefully written with two arrows going in reverse directions, as shown below.

\[ \ce{H2O (l) <=> H2O (g)} \]

Importantly, because there is a balance of opposing processes, this system can shift in response to external changes. For example, if the temperature decreased, the rate of evaporation would decrease more than  the rate of condensation and a new steady state pressure would be established that is lower than the original. This is why dew forms on surfaces near the ground during the evening; the rate of condensation exceeds that of evaporation so liquid water accumulates. Nature is rich in examples of equilibrium that serve as sensing mechanisms for organisms and that allow them to adjust to changing environments. Importantly, because there is a balance of opposing processes, the system corresponding to Figure 5-3 can shift in response to external changes. If the temperature decreased, for example, the rate of evaporation would decrease more than the rate of condensation and a new steady state pressure would be established that is lower than the original. Conversely, if the temperature were to increase, the rate of evaporation would increase more than the rate of condensation, increasing the steady state pressure of the water vapor.

The simple case of water evaporating and condensing is in some ways similar to how hemoglobin behaves, as well as to the competition between autoionization and neutralization that occurs in otherwise pure water. In all of these cases processes appear to partially react but reach steady state before the conversions are complete. In the latter case, when there is no hydronium or hydroxide in a sample of water, the rate of neutralization is necessarily small because there are no ions to be neutralized; the rate of autoionization is not so constrained and these ions are formed as shown in Figure 5-2. But when the concentrations of hydronium and hydroxide increase, the rate of neutralization increases, eventually equaling that of the autoionization and steady state is achieved. If on the other hand, we start with a solution that has high concentrations of both hydronium and hydroxide, the rate of neutralization far exceeds that of autoionization and the ions neutralize each other (Figure 5-4) far faster than autoionization regenerates them; as their concentrations fall, steady state is ultimately achieved when the rate of neutralization falls and eventually becomes equal to that of autoionization. In the case of hemoglobin, the rate of oxygen binding exceeds that of it dissociating when it is in the capillaries in the lungs, where oxygen is plentiful, but in internal tissues, where oxygen is scarce, the rate of dissociation exceeds that of oxygen binding. Thus the reversible binding of oxygen serves as a means for the protein to “sense” where it is and to serve its function as an oxygen transport molecule.

 

 

---

Footnotes and References

[1] Torricelli's Law states that the velocity, v, of a fluid flowing out from an opening is given by

\[ v = \sqrt{2gh} \nonumber \]

[1] Radiational heating is another term for "blackbody" radiation. All objects emit radiation by virtue of the fact that they are above absolute zero, and the greater the temperature, the more energy is radiated outwards. Objects at room temperature emit low energy infrared radiation, but warmer objects can emit visible light: the orange color of glowing embers and heating elements are examples, as is the visible light from the sun, whose surface is about 5,500°C.

[2] It is estimated that in the absence of any greenhouse gases the temperature of the earth would be about 30°C cooler, which would have the effect of greatly enlarging the polar regions and perhaps making the planet much less inhabitable.  

[3] A quick introduction to pressure: when gas molecules collide with the walls of whatever enclosure they are in, they impart a small force, just as if you were to strike a wall with a tennis ball. The force exerted by each particle is tiny indeed, but their cumulative effect can be quite large. By definition, pressure is defined as the force exerted by a fluid divided by the area over which it is exerted, or P = F/A; hence a common unit of pressure is pounds per square inch (psi). The pressure exerted by air at sea level is defined as 1 atmosphere (atm); 1 atm = 14.7 psi. Other units include the torr and the pascal (1 atm = 760 torr = 1.01×10⁵ pascals)