4.4: The Octet Rule, Valence, and Molecular Compounds

The emphasis in the preceding sections was on the formation of binary ionic compounds, i.e., those compounds that consist of one metallic and one nonmetallic constituent elements. But we have also previously encountered compounds that are composed exclusively of nonmetallic elements. This leads to an interesting problem: if nonmetals “want” to take electrons from their reaction partners, how can they react with other non-metals that want the same thing? Unlike the reactions between metals and nonmetals, which have “complimentary proclivities” as we described them earlier, if nonmetals all have the same proclivity, wouldn't that seem to preclude their reaction? Not at all. It would certainly make it very difficult for one of the reactants to completely remove electrons from the other, but not all reactions lead to the formation of ions. We saw in Chapter 3, atoms will “share” their electrons and form a chemical bond if doing so decreases their potential energy. We returned to this ideas briefly in section 4.2 when we stated that the electrons involved in the formation of bonds between nonmetals are shared, such as in the molecular forms of nonmetallic elements like N₂, P₄, or S₈, as well as in diamond and graphite.

The bonds between atoms of nonmetallic elements that consist of shared pairs of electrons are called covalent bonds and can exist between atoms of the same element, as in O₂ and H₂, or between atoms of different elements, as in H₂O. To recapitulate a key idea from Chapter 1: compounds that are composed solely of nonmetallic elements are usually molecular in nature. These compounds consist of discrete particles called molecules that are the smallest entities that exhibit the properties of the compound itself. Unlike an ionic arrangement where a given cation interacts with several anions which, in turn, interact with several cations, ad infinitum as in sodium chloride, in a molecule of CO₂ one carbon atom is tightly bonded to two and only oxygen atoms, which are tightly bonded only to that one carbon atom. They remain as a group, sometimes for decades, sometimes far longer, wandering aimlessly through the atmosphere [17]. Likewise, the hydrogen atoms in water are tightly bound to a central oxygen atom and they move as a trio through whatever medium in which they happen to reside.

 

Figure 4-14. How many molecules are in this diamond? Diamond is an example of a network solid and, as a result, this diamond consists of only one molecule. (Image credit: "Faceted diamond 1" by James St. John is licensed under CC BY 2.0.)

 

Molecules can vary in size from a mere two atoms [18], as we have seen with O₂ and H₂, to dozens, such as in linoleic acid, to hundreds of thousands or even millions, as in large biomolecules such as some proteins, DNA or cellulose, and synthetic polymers. There is, in fact, no limit to the number of atoms that can be in a single molecule. There are examples of atoms that are covalently linked into chains or three-dimensional networks that go one for what amounts to "infinity", at least in the sense that it seems to go on forever and there is no theoretical why such chains must terminate at any given point. Diamonds are a good example (Figure 4-14). The structure of diamond can be described as an "endless" network of carbon atoms in which each and every one of them (except those at the surface) is bound to four neighboring carbon atoms in a three-dimensional lattice, in which every carbon atom can be traced to every other carbon atoms via an unbroken sequence of covalent bonds (this accounts for the extremely high melting point). If it contained only carbon atoms, the entire universe could conceivably consist of a single diamond "molecule" (although such a universe would have to have evolved very differently than ours, which is rich in hydrogen and helium!). Many minerals, especially silicates, such as asbestos, mica and quartz, also form extended networks. Certain synthetic materials, such as vulcanized rubber also fall into this category. The concept of a “molecule” becomes less useful when considering such extended structures and these compounds are usually referred to as network solids rather than molecular compounds. (Question: How many molecules are in a car tire? Answer: One. Every atom in a tire is connected to every other by an uninterrupted sequence of chemical bonds, satisfying the definition of a “molecule”, albeit in an overly literal way.) How large does a molecule have to be before it becomes a network solid? No clear boundary between these two sorts of materials exists and the working definitions are often dependent on specific contexts.

When organizing the non-metallic elements into his Periodic Table, Mendeleev considered, among other things, the number of bonds they tend to make, referred to as their valence. A quick perusal of some simple oxygen-containing molecules (Figure 4-15) shows that the number of bonds oxygen has in water, two, is the same as in other structures. Note that when counting bonds, two single bonds is equivalent to one double bond. If we were to examine the thousands upon thousands of oxygen-containing compounds, we would find this is an overwhelming pattern: oxygen almost always forms two bonds when it combines with other atoms in molecules, especially when there is no "formal charge" associated with it [19]. Thus oxygen is said to have a valence of 2. Furthermore, recall from Chapter 1 that carbon typically makes four bonds, that is, it has a valence of four, and hydrogen has a valence of only one. You should readily see that these valences are all reflected in the structures in Figure 4-15. 

 

Figure 4-15. Examples of oxygen-containing molecules. Note that all oxygen atoms shown are connected to other atoms via two covalent bonds, either two separate single bonds, as in the case with water (top left), ethanol (bottom left) and the C-O-H portion of the carboxylic acid functional group in butyric acid (right), or one double bond, seen in O2 (top center), carbon dioxide (bottom center), or the carbonyl oxygen in butyric acid (right)

 

Mendeleev placed elements having the same valence in the same columns; thus sulfur, also with a valence of two, was placed in the same column as oxygen. At this point we can see a striking parallel between the valence of an element and the charge on its most common ionic form. Relating these separate ideas to the column number, n, is simple:

For a nonmetallic element in Column nA:

• its valence equals 8 - n
• its charge as a monatomic ion equals n - 8

To illustrate: oxygen, which is in Column 6A, has a valence of 2 and its ion has a charge of -2. Similarly, all elements in Column 7A, the halogens, have the same valence, 1, and the charge on the halide ions is -1. And carbon? It is in column 4A, so the above guideline would predict a valence of four which, as we've emphasized at several points, is indeed the number of bonds carbon usually makes. We should mention at this point, however, that carbon rarely, forms the monatomic ion, C^4-. It forms molecular compounds almost exclusively. 

Exercise 

Problem 4-5. What is the valence of the following nonmetallic elements? What is the charge on their corresponding monatomic ions?
    a) nitrogen            d) xenon
    b) sulfur                e) astatine
    c) iodine                f) phosphorus
 

An ensuing question to the above observations is: why does the valence of a nonmetal correspond so perfectly to its ionic charge?

Mendeleev did not have an answer into this question because its explanation requires insight into how the behavior of electrons behave in the formation of chemical bonds, specifically how they are either shared or transferred between atoms of various elements. But the electron had not been identified as a subatomic particle when Mendeleev developed the Periodic Table (making his achievement all the more remarkable!). In other words, Mendeleev knew nothing of electrons and based the organization of the Periodic Table only on the after-effects of their movement.

At this point it is probably useful to jump ahead a bit in terms of scientists' understanding of the electronic structure of atoms. With the advent of quantum mechanics, it became evident that the "electron cloud" is not unstructured or nebulous. Electrons do not exist as some formless, diffuse haze of negative charge centered around the nucleus as suggested by the Rutherford model. Rather, electrons actually exist in "layers" around the nucleus, akin to layers of an onion or the geologic layers of a planet, and only electrons in the outermost layer participate in bonding. You can rationalize this the following way: chemical reactions take place to lower the potential energy of the electrons of atoms; electrons that are close to their own nucleus (called core electrons) are already so deep in a potential energy well that they are already very stable and will not become more stable by being transferred to another atom. Electrons in the outer most layer (called valence electrons), however, have the weakest attraction to their nucleus and are vulnerable to being attracted to the nuclei of other atoms. Specifically, they are the electrons that can lower their potential energy if they can find another atom that has "space" closer to its nucleus.

How many valence electrons does a neutral atom of a given element have? For main group elements (recall these are the elements in columns 1A through 8A on the Periodic Table) the number of valence electrons equals the number of the column. In the second row, therefore, lithium, which is in column 1A, has one valence electron. Beryllium is in column 2A and has two valence electrons. The pattern continues throughout the row, ending up at neon which resides in Column 8A and has 8 valence electrons. All the inert gases have 8 valence electrons except helium, which as 2, a point that has some larger implications that will be discussed shortly.

 

Exercise

Problem 4-6. How many valence electrons are in neutral atoms of the following elements?

a) nitrogen               f) bromine
b) calcium                g) silicon
c) sulfur                   h) boron
d) arsenic                 i) lead
e) argon                   j) phosphorus

 

Given the above, we can relate the charges of monatomic ions in terms of valence electrons as follows:

• Metals form simple monatomic cations by losing all of their valence electrons.
• Nonmetals form monatomic anions by gaining additional valence electrons in the same number as their valence.

Focusing on nonmetals, the above point results in a recurring pattern: whether they form ionic compounds or molecular ones, the number of electrons that atoms of nonmetals end up with is the same: 8. This is known as the octet rule, one phrasing of which is, the number of valence electrons around atoms of nonmetallic elements in stable molecules tends to be eight. This is especially true of the elements carbon, nitrogen and oxygen, which is convenient as these elements form the basis of nearly all biologically important structures.[21] The major exception to this "rule" is hydrogen, which only forms one bond. When it does so, for example with oxygen in the case of water or carbon in the case of an alkane, it forms a bond by sharing two electrons - one of which is its own and the other is from the atom it is bonding with – thereby giving it two electrons in close proximity to its nucleus. Because hydrogen is such a ubiquitous element the octet rule is sometimes called the "inert gas electron configuration rule" (which, unfortunately, doesn't roll off the tongue nearly as well). This is a more general "rule" and states that when elements form bonds to make stable compounds they will end up with the same number of electrons as their nearest inert gas neighbor. Neon, which has 8 valence electrons, is the nearest neighbor of carbon, nitrogen and oxygen, so they will end up with 8 electrons, while helium, which as 2 valence electrons, is the nearest neighbor of hydrogen, so it ends up with 2. 

Representations of atoms and their valence electrons are often drawn as shown above (Figure 4-16), with dots representing the valence electrons that surround the elemental symbol. These diagrams are referred to as electron dot structures, or Lewis structures, in honor of the American chemist Gilbert Lewis, who proposed this simple approach in 1915. Electron dot structures for the component atoms of a water molecules are shown in Figure 4-16a. The hydrogen atoms are both shown with a single dot representing their sole valence electron, while the six valence electrons of oxygen are shown as two pairs and two single electrons; this illustrates the convention that, when drawing valence electrons, the first four are placed singly around the elemental symbol and each additional electron is paired with one (it doesn’t matter which) of the original four. Thus carbon would have four unpaired electrons (Figure 4-16b) and an inert gas like neon would have four pairs of electrons around the Ne symbol (Figure 4-16c). 

 

Figure 4-16: Electron dot structures of a) the component atoms of a molecule of water; b) a single carbon atom, and; c) a single neon atom. Note the convention of how valence electrons are depicted: the first four are drawn individually, as seen with carbon, while additional electrons are paired with those of the first set of four, as seen with oxygen (two such pairs) and neon (four pairs). 

 

Before discussing the application of the octet rule to molecular compounds, it would be useful to show first how it applies to ionic compounds since the previous section focused on those. Sodium chloride provides an good example. As discussed previously, the direct reaction of the elements results in the formation of sodium cations and chloride anions which coalesce in the form of crystals of sodium chloride. We can look at the reaction in terms of two separate steps, focusing on the gain or loss of electrons, depicted below as e^- in Figure 4-17, below. You can see that the chloride ion has eight valence electrons satisfying the octet rule.  

 

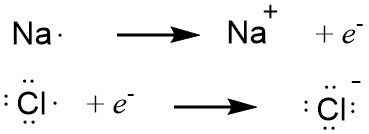
Figure 4-17. The formation of sodium cation (top) and chloride anion (bottom) by the gain and loss of an electron (represented by e^-), respectively. The electron written as a product in the top equation is the source of the electron written as a reactant in the bottom equation. Note that both of the ions that are formed obey the octet rule.

 

What about sodium? It starts with one valence electron and loses it. Wouldn't that mean the sodium ion has zero valence electrons and, if so, doesn't that violate the octet rule? Recall that the octet rule can also be stated as the inert gas electron configuration rule. Neutral sodium atoms have 11 electrons (because it has 11 protons), but the sodium cation has only 10 electrons. This is the same number of electrons as its nearest inert gas neighbor, neon. Eight of neon's ten electrons are valence electrons, and eight of the sodium ion's ten electrons can also be viewed as valence electrons. The onion analogy works here. Onions always have an outermost layer; if you peel away the outermost layer of an onion, the newly exposed layer becomes the new outermost layer. In the case of metal ions, if you strip away all the electrons of their valence level, the newly exposed layer of electrons becomes the new valence level and this will have the same number of electrons as the nearest inert gas neighbor (although it is extremely unreactive because they remain closer to the nucleus than the original valence level).

 

Exercise

Problem 4-7. Explain how the ions of calcium oxide follow the octet rule.

 

The utility of electron dot structures is that they provide a framework with which you can “build” molecules. The basic premise is simple: atoms are connected by making pairs of lone, or unpaired, valence electrons in such a way as to surround themselves with a total of eight of them (with the exception of hydrogen, as mentioned above, which only can accommodate two). A few simple examples will help illustrate the idea and demonstrate its utility. We mentioned above that molecules of halogens are diatomic; fluorine exists as F₂, for instance, and the electron dot structure of fluorine (Figure 4-18a) shows why. Consider two separate neutral fluorine atoms, each having only 7 valence electrons. They can both can satisfy their octets by by pairing their own lone electron with that of the other, thereby forming a covalent bond between the two atoms. It is important to understand the counting scheme employed here: there are only 14 total valence electrons in the molecule, but we say that each fluorine atom in F₂ “has” 8. That language could imply that the total number of electrons is 16, but it is simply a convenient way of expressing the fact that each fluorine nucleus directly interacts with 8 valence electrons.  As we described earlier, this type of bond formation is driven by the decrease in potential energy that results from having the bonding electrons interact simultaneously with two separate nuclei. This example also provides an example of how the concept of valence reinforces the picture that emerged using electron dot structures. Fluorine, in Column 7A has seven valence electrons and therefore has a valence of one, so we expect to see each fluorine atoms make one bond, which it can do when making F₂.

Electron dot structures and valence considerations also reveal why fluorine does not form molecules such as F₃ or F₄, as such combinations are impossible without exceeding fluorine’s octet (Figure 4-18b) or forming more than one bond for at least some fluorine atoms. Energetically speaking, such a combination does not lower the potential energy of the fluorine atoms as much as the formation of F₂ and, as result, fluorine atoms will always form F₂ instead of the less stable F₃. Electron dot structures make such behavior simple to predict.

Figure 4-18. a) Electron dot structures of two fluorine atoms, each with 7 valence electrons; the octet of each atom is achieved in by the formation of F2 when the lone electrons on each atom pair up (shown by the dashed loop) to form a covalent bond. A balanced chemical equation that describes the reaction is shown below the electron dot depictions. b) Two futile attempt to build an F3 molecule: (top) the lone electron on the far right F atom pairs with an already paired electron on the central F, resulting in the latter’s exceeding its octet by one electron, a very destabilizing scenario; (bottom) an alternative proposal in which a covalent bond consisting of three electrons is formed (this would represent one and one-half bonds, a midpoint between single and double bonds). As we will see such fractional bonds are not inherently problematic, but this arrangement gives the two fluorine atoms so bonded each 9 electrons, which is definitely problematic. In both attempts, the normal valence (which is 1) of the central fluorine is not obeyed.

 

The above treatment can be used to explain other diatomic structures. All of the halogens have seven valence electrons, thus the above discussion would be identical for chlorine, bromine and iodine. Hydrogen, with a single valence electron, achieves its dyad (as opposed to an octet) by pairing with one and only one other hydrogen atom. Nitrogen and oxygen also form diatomic molecules to achieve their octets and, in accord with their valences of 3 and 2, respectively, do so via triple and double bonds, respectively. We'll return to these molecules shortly to show how you can illustrate multiple bonds with electron dot diagrams. 

 

Example 

Problem 4-8. Using electron dot structures, show how a neutral atom of hydrogen might react with a neutral atom of fluorine. Explain the formation of the product in terms of changes in potential energy.

 

At a Glance: Valence & The Octet Rule

We pause here to emphasize a useful point: an element's valence is a direct consequence of how it obeys the octet rule. The above prediction that fluorine atoms should form F₂ molecules, which we based on the octet rule, could have also been made using using the concept of valence: the only way to build a fluorine molecule that satisfies each fluorine atom’s valence of one is to join two such atoms by a single bond. Any other structure would demand a valence greater than one. Recall that Mendeleev did not know about electrons and therefore had no inkling concerning the octet rule, but the manifestation of the octet rule – valence – was visible to him and he used it in the development of the Periodic Table.

The valence of biologically important elements, and how they relate to the octet rule is summarized below.

Element	Column Number on Periodic Table*	Number of Valence Electrons	Number of Electrons Needed to Complete Octet	Valence
H	1A	1	1**	1
C	4A	4	4	4
N	5A	5	3	3
O	6A	6	2	2
Notes: *   These columns labels are those used in Figure 4-2 and are not those recommended by IUPAC (see note footnote 1 in section 4.1) **  As stated in the text, hydrogen doesn't follow the "octet" rule but accommodates two electrons to complete its valence shell, the same as helium.

 

We can now illustrate how the octet rule applies to some simple molecules and, in the process, finally address the question we opened this chapter with: why hydrogen and oxygen react to form H₂O but not H₃O? To start, you need to consider each individual atom and its valence electrons: in this case we have two hydrogen atoms, each with one valence electron (it is in Column 1A), and one oxygen atom, with six (it being in Column 6A). Figure 4-19 (top) shows a simple electron dot structure for water where each of the unpaired electrons of oxygen are paired with electrons from hydrogen.  

 

Figure 4-19: (top) Electron dot structures of the component atoms of water; the dashed loop shows how the unpaired electrons come together to form two covalent bonds. (bottom) Four different electron dot structures of water. The two on the left show all electrons pairs. there are two bonding and two non-bonding pairs of electrons in water; the only difference between them is the use of color which can help illustrate the atom of origin of each electron. The two on the right show bonding pairs as lines. The structure on the far right omits the non-bonding electron pairs, or lone pairs, on the oxygen atom; this is the most common way of depicting molecular structures and requires the reader to be cognizant of the presence of lone pairs even though they are not shown.

 

The four structures on the bottom of Figure 4-19 provide examples of how electron dot structures are frequently presented. The structure at the far left uses color to distinguish the electrons originally associated with hydrogen (red) and oxygen (blue). The monochromatic version, to the right, shows the same interactions between the atoms, but obscures the origins of the electrons; this is not a problem in practice because once a molecule forms, the electrons get “mixed in the pot” and are indistinguishable from each other. The third structure depicts the covalent bonds as lines between each atom, the same way we originally showed them in Chapter 1, and also shows the unshared pairs of electrons_, also called lone pairs, on the oxygen. This depiction makes it easy to confirm that the oxygen atom obeys the octet rule: each bond contributes two and electrons as does each lone pair. The version on the far right omits the lone pairs of electrons on the oxygen atom. These two pairs of electrons do not participate in covalent bonding and are frequently omitted from molecular structures for that reason. It is critical to note, however, that their presence has a large effect on the structure of molecules and can often play a key role in reaction chemistry, so it is important to recognize when they are present, even if they are not shown in a particular figure. If you go back to the structure of linoleic acid shown in Chapter 1, you will note no lone pairs were explicitly shown on the oxygen atoms but each of them has two such pairs of nonbonding electrons, just as in the right-hand structure of water in Figure 4-19. It is simply a consequence of having six valence electrons and the requisite formation of two covalent bonds to achieve an octet. Thus the omission of lone pairs should not be a worrisome feature in dot structures and you will quickly get accustomed to mentally “filling them in” as necessary.

It should be clear now why a neutral molecule such as H₃O violates the octet rule. Just as we could not combine three fluorine atoms to form an F₃ molecule that did not exceed the octet of at least one fluorine atom, a third hydrogen atom cannot share its electron with oxygen without exceeding the latter’s octet. Nor can it form a bond with one of the other hydrogen atoms without exceeding one of the dyads. Likewise, the simple diatomic molecule OH also fails to satisfy the octet rule, with oxygen having only seven electrons. Chemical species that have unpaired electrons, such as neutral OH, such as this are known as radicals and are often unstable on account of their incomplete octets. This particular species is known as the hydroxyl radical and forms in small amounts in the course of normal biochemical processes, including aerobic respiration; it is highly reactive for reasons you may surmise: the oxygen can accommodate an additional electron and it will react readily to obtain one. It is this high reactivity that makes it a problematic species for living organisms: the hydroxyl radical has been linked to numerous negative health effects, including many symptoms of aging, all due to undesired reactions that result from oxygen’s ravenous appetite for that eighth electron. An example of its chemical reactivity is discussed below.

Given what we have presented thus far, it is possible to predict at least one reaction pathway followed by the hydroxyl radical. Both the hydroxyl radical and the neutral fluorine atom have seven valence electrons and, as a result, can achieve their octets by reacting similarly. Species such as these, which have the same arrangement of valence electrons, are termed isoelectronic and often show similar bonding and/or reactivity patterns. Consider two hydroxyl radicals that are in close proximity: each has seven electrons around the oxygen, one of which is unpaired and is therefore available to form a bond. These two radicals can couple, or dimerize (a dimer is a molecule that consists of two identical fragments) to form hydrogen peroxide, H₂O₂, in which the octet is achieved for both oxygen atoms (Figure 4-20). This is totally analogous to the behavior of fluorine atoms as they too will dimerize to form F₂.

 

Figure 4-20. Dimerization of hydroxyl radicals; each hydroxyl radical has only seven electrons, but by pairing their lone electrons, two hydroxyl radicals achieve their octets and a molecule of hydrogen peroxide, H₂O₂, is formed.

 

The obvious parallels between the tendency of the hydroxyl radical to dimerize and fluorine’s tendency to form F₂ serves as an illustration that electron dot structures are useful to understand not only what molecules “make sense”, but on how species may interact chemically. Of course, fluorine atoms and hydroxyl radicals have important differences as well, so simply knowing how many valence electrons a species has is not enough to get a clear picture of its behavior under specific conditions, but it is an exceptionally useful starting point when thinking about such questions.

Before moving on to a discussion of Lewis structures of organic molecules, it would be useful to examine how multiple bonds are represented. We’ve already stated that elemental oxygen consists of O₂ molecules bonded together with a double bond. Recall that a double bond consists of two shared pairs of electrons. While a fairly reactive gas (we wouldn’t be alive if it wasn’t), both oxygen atoms in O₂ have complete octets. The sharing of two pairs of electrons is illustrated in Figure 4-21 (left). Beginning with two isolated oxygen atoms, each with six valence electrons, you can easily see that a single bond could be formed by pairing one unpaired electron on each of them (top, left); this singly bonded O₂ molecule would violate the octet rule as both oxygen atoms have only seven electrons (center, left). By pairing the remaining lone electrons on each oxygen, a second covalent bond is formed and both atoms achieve their octets (bottom structure). Identical logic holds in the case of N₂, except that in this case each nitrogen atom begins with only five valence electrons, thus three covalent bonds are needed to satisfy their octets, and a triple bond is formed (Figure 4-21, right). Note once again how these structures follow the expected valences of oxygen and nitrogen.

 

Figure 4-21: “Building” Lewis structures of O₂ and N₂. To illustrate electron pairing, the bonds are formed sequentially in this depiction by pairing electrons enclosed in the dashed loops. The final structures (at the bottom of each column) have complete octets and the expected valences for each element. Left: Each oxygen atom satisfies its octet by pairing its lone electrons in the formation of a double bond, as would be predicted by its valence of two. Right: Nitrogen, with a valence of three, forms a triple bond by pairing all of its lone electrons with those of another nitrogen atom.

 

We close this section by taking a step back to consider the octet rule in a broader context. Specifically, in the formation of ionic and molecular compounds, why do atoms tend to end up with the same number of electrons as their closest inert gas neighbor? Consider the following thought experiment. You have a collection of atoms of different elements that are all neutral and all isolated from each other, each having electrons and protons in equal quantities but where no bonds exist between atoms; as they begin to collide with each other, what will happen? You should recognize that the initial arrangement of particles is not the most stable arrangement of electrons and nuclei. Such a collection has higher potential energy than an arrangement where the atoms gain, lose or share electrons in such a way that they end up the same number of valence electrons as their closest inert gas neighbors. As such, the atoms of metallic elements will tend to lose electrons to atoms of nonmetallic elements, generating ionic compounds, and atoms of nonmetals will share electrons and form covalent bonds as part of molecular compounds, and the octet rule will guide how these compounds form. Atoms of the inert gases, however, will be the only ones that will not react as they collide with other atoms. This implies a connection between energy and the octet rule. But what is it, specifically? This is worthy line of inquiry, and one we will address soon. But for now, the observation that inert gases are just that, inert, is another indication that there is something peculiar about that particular arrangement of electrons: inert gases are inert because they have such a low potential energy in their elemental forms that altering them in some way would usually increases their potential energy and hence is unfavorable.  We conclude that species with such electron counts occupy low spots on the energetic landscape; just as water collects in the low spots on an actual landscape, because those are the locales of minimum potential energy, so too do atoms tend to arrange themselves in patterns that minimize potential energy.

 

 

 

---

Problems. 

4-9. Draw electron dot structures for the following fluorine-containing compounds:
    a) hydrogen fluoride (HF)
    b) chlorine monofluoride (ClF)
    c) carbon tetrafluoride (CF₄)
    d) nitrogen trifluoride (NF₃)
    e) oxygen difluoride (OF₂)

4-10. Draw electron dot structures of the following hydrogen-containing compounds:
    a) ammonia (NH₃)
    b) phosphine (PH₃)
    c) hydrogen sulfide (H₂S)
    d) silane (SiH₄)

4-11. Inorganic carbon. Draw electron dot structures for the following compounds that contain only carbon and oxygen (these are two forms of so-called “inorganic carbon”):
    a) carbon dioxide (CO₂) - this one is fairly straightforward.
    b) carbon monoxide (CO) - this one is trickier. Hint: both C and O obey the octet rule in this compound, but neither follows its normal valence. Another hint: what molecule have you seen is isoelectronic with CO? 

4-12. Something to ponder. What does the example of CO imply about which is the more fundamental principle: that elements have a specific valence, or that potential energy is minimized by achieving octets of valence electrons? In other words, which of these general “rules” is a consequence of the other?

 

---

Notes and References.

[17] A beautiful essay entitled "Carbon" wraps up Primo Levi's haunting memoir, "The Periodic Table". The entire book is highly recommended, but the culminating essay is worth reading on its own too. In it, he follows the path of a single carbon atoms as it escapes being trapped in the form calcium carbonate, becomes airborne in the form of CO₂, is trapped by a green plant and converted into a sugar that ultimately provides the author with the energy to put into place the period at the final sentence of the book.

[18] Some chemists consider single atoms of inert gases as molecules too. For example, they might refer to a "molecule" of argon, which consists of just one atom of argon.

[19] Formal charge is a very useful way of counting electrons in molecules because it correlates extremely well with certain reactivity patterns. Oxygen has a formal charge of zero in water because it has two bonds, but -1 in hydroxide, where it only has one bond, and +1 in hydronium where it has three bonds. Thus oxygen can have more than or fewer than two bonds in certain molecular species, but these will often be much more reactive. We will discuss formal charge and how to determine it later. 

[20] Formal charge is a very useful way of counting electrons in molecules because it correlates extremely well with certain reactivity patterns. Oxygen has a formal charge of zero in water because it has two bonds, but -1 in hydroxide, where it only has one bond, and +1 in hydronium where it has three bonds. Thus oxygen can have more than or fewer than two bonds in certain molecular species, but these will often be much more reactive. We will discuss formal charge and how to determine it later. 

[21] The statement that the octet rule is especially followed by carbon, nitrogen and oxygen implies that there are other elements that do not follow it quite as regularly. This is true. Of particular importance are elements in the third row of the periodic table, notably phosphorus, sulfur and chlorine. These elements frequently "expand" their octets and can accommodate as many as 18 electrons, although those are extreme cases. But 10 or 12 electrons around these elements are not uncommon under some conditions. For example, in the polyatomic ions phosphate (PO₄^3-) and sulfate (SO₄^2-) both are commonly viewed as having more than an octet. We'll explain more fully when we discuss the electronic structure of atoms in more detail.