1.6: Gas Mixtures and Partial Pressures
- Page ID
- 164732
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Skills to Develop
- To determine the contribution of each component gas to the total pressure of a mixture of gases
In our use of the ideal gas law thus far, we have focused entirely on the properties of pure gases with only a single chemical species. But what happens when two or more gases are mixed? In this section, we describe how to determine the contribution of each gas present to the total pressure of the mixture.
Partial Pressures
The ideal gas law assumes that all gases behave identically and that their behavior is independent of attractive and repulsive forces. If volume and temperature are held constant, the ideal gas equation can be rearranged to show that the pressure of a sample of gas is directly proportional to the number of moles of gas present:
\[P=n \left(\dfrac{RT}{V}\right) = n \times \rm const. \label{10.6.1}\]
Nothing in the equation depends on the identity of the gas—only the amount.
With this assumption, let’s suppose we have a mixture of two ideal gases that are present in equal amounts. What is the total pressure of the mixture? Because the pressure depends on only the total number of particles of gas present, the total pressure of the mixture will simply be twice the pressure of either component. More generally, the total pressure exerted by a mixture of gases at a given temperature and volume is the sum of the pressures exerted by each gas alone. Furthermore, if we know the volume, the temperature, and the number of moles of each gas in a mixture, then we can calculate the pressure exerted by each gas individually, which is its partial pressure, the pressure the gas would exert if it were the only one present (at the same temperature and volume).
To summarize, the total pressure exerted by a mixture of gases is the sum of the partial pressures of component gases. This law was first discovered by John Dalton, the father of the atomic theory of matter. It is now known as Dalton’s law of partial pressures. We can write it mathematically as
\[P_{tot}= P_1+P_2+P_3+P_4 \; ... = \sum_{i=1}^n{P_i} \label{10.6.2}\]
where \(P_{tot}\) is the total pressure and the other terms are the partial pressures of the individual gases (up to \(n\) component gases).

For a mixture of two ideal gases, \(A\) and \(B\), we can write an expression for the total pressure:
\[P_{tot}=P_A+P_B=n_A\bigg(\dfrac{RT}{V}\bigg) + n_B\bigg(\dfrac{RT}{V}\bigg)=(n_A+n_B)\bigg(\dfrac{RT}{V}\bigg) \label{10.6.3}\]
More generally, for a mixture of \(n\) component gases, the total pressure is given by
\[P_{tot}=(P_1+P_2+P_3+ \; \cdots +P_n)\bigg(\dfrac{RT}{V}\bigg)\label{10.6.2a}\]
\[P_{tot}=\sum_{i=1}^n{n_i}\bigg(\dfrac{RT}{V}\bigg)\label{10.6.2b}\]
Equation \(\ref{10.6.2b}\) restates Equation \(\ref{10.6.3}\) in a more general form and makes it explicitly clear that, at constant temperature and volume, the pressure exerted by a gas depends on only the total number of moles of gas present, whether the gas is a single chemical species or a mixture of dozens or even hundreds of gaseous species. For Equation \(\ref{10.6.2b}\) to be valid, the identity of the particles present cannot have an effect. Thus an ideal gas must be one whose properties are not affected by either the size of the particles or their intermolecular interactions because both will vary from one gas to another. The calculation of total and partial pressures for mixtures of gases is illustrated in Example \(\PageIndex{1}\).
Example \(\PageIndex{1}\): The Bends
Deep-sea divers must use special gas mixtures in their tanks, rather than compressed air, to avoid serious problems, most notably a condition called “the bends.” At depths of about 350 ft, divers are subject to a pressure of approximately 10 atm. A typical gas cylinder used for such depths contains 51.2 g of \(O_2\) and 326.4 g of He and has a volume of 10.0 L. What is the partial pressure of each gas at 20.00°C, and what is the total pressure in the cylinder at this temperature?
Given: masses of components, total volume, and temperature
Asked for: partial pressures and total pressure
Strategy:
- Calculate the number of moles of \(He\) and \(O_2\) present.
- Use the ideal gas law to calculate the partial pressure of each gas. Then add together the partial pressures to obtain the total pressure of the gaseous mixture.
Solution:
A The number of moles of \(He\) is
\[n_{\rm He}=\rm\dfrac{326.4\;g}{4.003\;g/mol}=81.54\;mol\]
The number of moles of \(O_2\) is
\[n_{\rm O_2}=\rm \dfrac{51.2\;g}{32.00\;g/mol}=1.60\;mol\]
B We can now use the ideal gas law to calculate the partial pressure of each:
\[P_{\rm He}=\dfrac{n_{\rm He}RT}{V}=\rm\dfrac{81.54\;mol\times0.08206\;\dfrac{atm\cdot L}{mol\cdot K}\times293.15\;K}{10.0\;L}=196.2\;atm\]
\[P_{\rm O_2}=\dfrac{n_{\rm O_2} RT}{V}=\rm\dfrac{1.60\;mol\times0.08206\;\dfrac{atm\cdot L}{mol\cdot K}\times293.15\;K}{10.0\;L}=3.85\;atm\]
The total pressure is the sum of the two partial pressures:
\[P_{\rm tot}=P_{\rm He}+P_{\rm O_2}=\rm(196.2+3.85)\;atm=200.1\;atm\]
Exercise \(\PageIndex{1}\)
A cylinder of compressed natural gas has a volume of 20.0 L and contains 1813 g of methane and 336 g of ethane. Calculate the partial pressure of each gas at 22.0°C and the total pressure in the cylinder.
- Answer
-
\(P_{CH_4}=137 \; atm\); \(P_{C_2H_6}=13.4\; atm\); \(P_{tot}=151\; atm\)
Mole Fractions of Gas Mixtures
The composition of a gas mixture can be described by the mole fractions of the gases present. The mole fraction (\(X\)) of any component of a mixture is the ratio of the number of moles of that component to the total number of moles of all the species present in the mixture (\(n_{tot}\)):
\[x_A=\dfrac{\text{moles of A}}{\text{total moles}}= \dfrac{n_A}{n_{tot}} =\dfrac{n_A}{n_A+n_B+\cdots}\label{10.6.5}\]
The mole fraction is a dimensionless quantity between 0 and 1. If \(x_A = 1.0\), then the sample is pure \(A\), not a mixture. If \(x_A = 0\), then no \(A\) is present in the mixture. The sum of the mole fractions of all the components present must equal 1.
To see how mole fractions can help us understand the properties of gas mixtures, let’s evaluate the ratio of the pressure of a gas \(A\) to the total pressure of a gas mixture that contains \(A\). We can use the ideal gas law to describe the pressures of both gas \(A\) and the mixture: \(P_A = n_ART/V\) and \(P_{tot} = n_tRT/V\). The ratio of the two is thus
\[\dfrac{P_A}{P_{tot}}=\dfrac{n_ART/V}{n_{tot}RT/V} = \dfrac{n_A}{n_{tot}}=x_A \label{10.6.6}\]
Rearranging this equation gives
\[P_A = x_AP_{tot} \label{10.6.7}\]
That is, the partial pressure of any gas in a mixture is the total pressure multiplied by the mole fraction of that gas. This conclusion is a direct result of the ideal gas law, which assumes that all gas particles behave ideally. Consequently, the pressure of a gas in a mixture depends on only the percentage of particles in the mixture that are of that type, not their specific physical or chemical properties. By volume, Earth’s atmosphere is about 78% \(N_2\), 21% \(O_2\), and 0.9% \(Ar\), with trace amounts of gases such as \(CO_2\), \(H_2O\), and others. This means that 78% of the particles present in the atmosphere are \(N_2\); hence the mole fraction of \(N_2\) is 78%/100% = 0.78. Similarly, the mole fractions of \(O_2\) and \(Ar\) are 0.21 and 0.009, respectively. Using Equation 10.6.7, we therefore know that the partial pressure of N2 is 0.78 atm (assuming an atmospheric pressure of exactly 760 mmHg) and, similarly, the partial pressures of \(O_2\) and \(Ar\) are 0.21 and 0.009 atm, respectively.
Example \(\PageIndex{2}\): Exhaling Composition
We have just calculated the partial pressures of the major gases in the air we inhale. Experiments that measure the composition of the air we exhale yield different results, however. The following table gives the measured pressures of the major gases in both inhaled and exhaled air. Calculate the mole fractions of the gases in exhaled air.
| Inhaled Air / mmHg | Exhaled Air / mmHg | |
|---|---|---|
| \(P_{\rm N_2}\) | 597 | 568 |
| \(P_{\rm O_2}\) | 158 | 116 |
| \(P_{\rm H_2O}\) | 0.3 | 28 |
| \(P_{\rm CO_2}\) | 5 | 48 |
| \(P_{\rm Ar}\) | 8 | 8 |
| \(P_{tot}\) | 767 | 767 |
Given: pressures of gases in inhaled and exhaled air
Asked for: mole fractions of gases in exhaled air
Strategy:
Calculate the mole fraction of each gas using Equation \(\ref{10.6.7}\).
Solution:
The mole fraction of any gas \(A\) is given by
\[x_A=\dfrac{P_A}{P_{tot}}\]
where \(P_A\) is the partial pressure of \(A\) and \(P_{tot}\) is the total pressure. For example, the mole fraction of \(CO_2\) is given as:
\[x_{\rm CO_2}=\rm\dfrac{48\;mmHg}{767\;mmHg}=0.063\]
The following table gives the values of \(x_A\) for the gases in the exhaled air.
| Gas | Mole Fraction |
|---|---|
| \({\rm N_2}\) | 0.741 |
| \({\rm O_2}\) | 0.151 |
| \({\rm H_2O}\) | 0.037 |
| \({\rm CO_2}\) | 0.063 |
| \({\rm Ar}\) | 0.010 |
Exercise \(\PageIndex{2}\)
Venus is an inhospitable place, with a surface temperature of 560°C and a surface pressure of 90 atm. The atmosphere consists of about 96% CO2 and 3% N2, with trace amounts of other gases, including water, sulfur dioxide, and sulfuric acid. Calculate the partial pressures of CO2 and N2.
- Answer:
-
\[P_{\rm CO_2}=\rm86\; atm\]
\[P_{\rm N_2}=\rm2.7\;atm\]
Collection of Gases over Water
A simple laboratory method to collect gases that do not react with water is to capture them in a bottle that has been filled with water and inverted into a dish filled with water. The pressure of the gas inside the bottle can be made equal to the air pressure outside by raising or lowering the bottle. When the water level is the same both inside and outside the bottle (Figure \(\PageIndex{2}\)), the pressure of the gas is equal to the atmospheric pressure, which can be measured with a barometer.
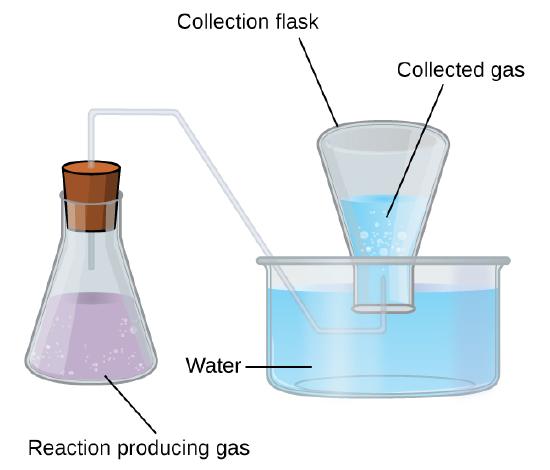
Figure \(\PageIndex{2}\): When a reaction produces a gas that is collected above water, the trapped gas is a mixture of the gas produced by the reaction and water vapor. If the collection flask is appropriately positioned to equalize the water levels both within and outside the flask, the pressure of the trapped gas mixture will equal the atmospheric pressure outside the flask (see the earlier discussion of manometers).
However, there is another factor we must consider when we measure the pressure of the gas by this method. Water evaporates and there is always gaseous water (water vapor) above a sample of liquid water. As a gas is collected over water, it becomes saturated with water vapor and the total pressure of the mixture equals the partial pressure of the gas plus the partial pressure of the water vapor. The pressure of the pure gas is therefore equal to the total pressure minus the pressure of the water vapor—this is referred to as the “dry” gas pressure, that is, the pressure of the gas only, without water vapor.
The vapor pressure of water, which is the pressure exerted by water vapor in equilibrium with liquid water in a closed container, depends on the temperature (Figure \(\PageIndex{3}\)); more detailed information on the temperature dependence of water vapor can be found in Table \(\PageIndex{1}\), and vapor pressure will be discussed in more detail in the next chapter on liquids.
| Temperature (°C) | Pressure (torr) | Temperature (°C) | Pressure (torr) | Temperature (°C) | Pressure (torr) | ||
|---|---|---|---|---|---|---|---|
| –10 | 1.95 | 18 | 15.5 | 30 | 31.8 | ||
| –5 | 3.0 | 19 | 16.5 | 35 | 42.2 | ||
| –2 | 3.9 | 20 | 17.5 | 40 | 55.3 | ||
| 0 | 4.6 | 21 | 18.7 | 50 | 92.5 | ||
| 2 | 5.3 | 22 | 19.8 | 60 | 149.4 | ||
| 4 | 6.1 | 23 | 21.1 | 70 | 233.7 | ||
| 6 | 7.0 | 24 | 22.4 | 80 | 355.1 | ||
| 8 | 8.0 | 25 | 23.8 | 90 | 525.8 | ||
| 10 | 9.2 | 26 | 25.2 | 95 | 633.9 | ||
| 12 | 10.5 | 27 | 26.7 | 99 | 733.2 | ||
| 14 | 12.0 | 28 | 28.3 | 100.0 | 760.0 | ||
| 16 | 13.6 | 29 | 30.0 | 101.0 | 787.6 |
Example \(\PageIndex{3}\): Pressure of a Gas Collected Over Water
If 0.200 L of argon is collected over water at a temperature of 26 °C and a pressure of 750 torr in a system like that shown in Figure \(\PageIndex{2}\), what is the partial pressure of argon?
Solution
According to Dalton’s law, the total pressure in the bottle (750 torr) is the sum of the partial pressure of argon and the partial pressure of gaseous water:
Rearranging this equation to solve for the pressure of argon gives:
The pressure of water vapor above a sample of liquid water at 26 °C is 25.2 torr, so:
Exercise \(\PageIndex{3}\)
A sample of oxygen collected over water at a temperature of 29.0 °C and a pressure of 764 torr has a volume of 0.560 L. What volume would the dry oxygen have under the same conditions of temperature and pressure?
- Answer
-
0.583 L
The pressure of a gas collected over water after a chemical reaction must always be corrected by subtracting the vapor pressure of water from the total, based on the temperature.
Example \(\PageIndex{4}\): Emergency Air bags
Sodium azide (\(NaN_3\)) decomposes to form sodium metal and nitrogen gas according to the following balanced chemical equation:
\[\ce{ 2NaN3 \rightarrow 2Na(s) + 3N2(g)}\]
This reaction is used to inflate the air bags that cushion passengers during automobile collisions. The reaction is initiated in air bags by an electrical impulse and results in the rapid evolution of gas. If the \(N_2\) gas that results from the decomposition of a 5.00 g sample of \(NaN_3\) were collected over water, what volume of gas would be produced at 21°C and 762 mmHg?
Given: reaction, mass of compound, temperature, and pressure
Asked for: volume of nitrogen gas produced
Strategy:
A Calculate the number of moles of N2 gas produced. From the data in Table 10.5.4, determine the partial pressure of N2 gas in the flask.
B Use the ideal gas law to find the volume of N2 gas produced.
Solution:
A Because we know the mass of the reactant and the stoichiometry of the reaction, our first step is to calculate the number of moles of N2 gas produced:
\[\rm\dfrac{5.00\;g\;NaN_3}{(22.99+3\times14.01)\;g/mol}\times\dfrac{3mol\;N_2}{2mol\;NaN_3}=0.115\;mol\; N_2 \]
The pressure given (762 mmHg) is the total pressure in the flask, which is the sum of the pressures due to the N2 gas and the water vapor present. Table 10.5.4 tells us that the vapor pressure of water is 18.65 mmHg at 21°C (294 K), so the partial pressure of the N2 gas in the flask is only
\[\rm(762 − 18.65)\;mmHg \times\dfrac{1\;atm}{760\;atm}= 743.4\; mmHg \times\dfrac{1\;atm}{760\;atm}= 0.978\; atm. \]
B Solving the ideal gas law for V and substituting the other quantities (in the appropriate units), we get
\[V=\dfrac{nRT}{P}=\rm\dfrac{0.115\;mol\times0.08206\dfrac{atm\cdot L}{mol\cdot K}\times294\;K}{0.978\;atm}=2.84\;L \]
Exercise\(\PageIndex{4}\)
A 1.00 g sample of zinc metal is added to a solution of dilute hydrochloric acid. It dissolves to produce H2 gas according to the equation
\[\ce{ Zn(s) + 2 HCl(aq) → H2(g) + ZnCl2(aq)}.\]
The resulting H2 gas is collected over water at 30°C and an atmospheric pressure of 760 mmHg. What volume does it occupy?
- Answer
-
0.397 L
Summary
The partial pressure of each gas in a mixture is proportional to its mole fraction. The pressure exerted by each gas in a gas mixture (its partial pressure) is independent of the pressure exerted by all other gases present. Consequently, the total pressure exerted by a mixture of gases is the sum of the partial pressures of the components (Dalton’s law of partial pressures). The amount of gas present in a mixture may be described by its partial pressure or its mole fraction. The mole fraction of any component of a mixture is the ratio of the number of moles of that substance to the total number of moles of all substances present. In a mixture of gases, the partial pressure of each gas is the product of the total pressure and the mole fraction of that gas.
In the laboratory, gases produced in a reaction are often collected by the displacement of water from filled vessels; the amount of gas can then be calculated from the volume of water displaced and the atmospheric pressure. A gas collected in such a way is not pure, however, but contains a significant amount of water vapor. The measured pressure must therefore be corrected for the vapor pressure of water, which depends strongly on the temperature.
Contributors
Paul Flowers (University of North Carolina - Pembroke), Klaus Theopold (University of Delaware) and Richard Langley (Stephen F. Austin State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110).
- Anna Christianson, Bellarmine University

