6.7: The Second Law of Thermodynamics - Entropy
- Page ID
- 98560
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Skills to Develop
- To understand the relationship between internal energy and entropy.
- To calculate entropy changes for a chemical reaction
The first law of thermodynamics governs changes in the state function we have called internal energy (\(U\)). Changes in the internal energy (ΔU) are closely related to changes in the enthalpy (ΔH), which is a measure of the heat flow between a system and its surroundings at constant pressure. You also learned that the enthalpy change for a chemical reaction can be calculated using tabulated values of enthalpies of formation. This information, however, does not tell us whether a particular process or reaction will occur spontaneously.
Let’s consider a familiar example of spontaneous change. If a hot frying pan that has just been removed from the stove is allowed to come into contact with a cooler object, such as cold water in a sink, heat will flow from the hotter object to the cooler one. Eventually both objects will reach the same temperature, at a value between the initial temperatures of the two objects. This transfer of heat from a hot object to a cooler one obeys the first law of thermodynamics: energy is conserved.
Now consider the same process in reverse. Suppose that a hot frying pan in a sink of cold water were to become hotter while the water became cooler. As long as the same amount of thermal energy was gained by the frying pan and lost by the water, the first law of thermodynamics would be satisfied. Yet we all know that such a process cannot occur: heat always flows from a hot object to a cold one, never in the reverse direction. That is, by itself, the magnitude of the heat flow associated with a process does not predict whether the process will occur spontaneously.
For many years, chemists and physicists tried to identify a single measurable quantity that would enable them to predict whether a particular process or reaction would occur spontaneously. Initially, many of them focused on enthalpy changes and hypothesized that an exothermic process would always be spontaneous. But although it is true that many, if not most, spontaneous processes are exothermic, there are also many spontaneous processes that are not exothermic. For example, at a pressure of 1 atm, ice melts spontaneously at temperatures greater than 0°C, yet this is an endothermic process because heat is absorbed. Similarly, many salts (such as NH4NO3, NaCl, and KBr) dissolve spontaneously in water even though they absorb heat from the surroundings as they dissolve (i.e., ΔHsoln > 0). Reactions can also be both spontaneous and endothermic, like the reaction of barium hydroxide with ammonium thiocyanate shown in Figure \(\PageIndex{1}\).

Figure \(\PageIndex{1}\): An Endothermic Reaction. The reaction of barium hydroxide with ammonium thiocyanate is spontaneous but highly endothermic, so water, one product of the reaction, quickly freezes into slush. For a full video: see https://www.youtube.com/watch?v=GQkJI-Nq3Os.
Thus enthalpy is not the only factor that determines whether a process is spontaneous. For example, after a cube of sugar has dissolved in a glass of water so that the sucrose molecules are uniformly dispersed in a dilute solution, they never spontaneously come back together in solution to form a sugar cube. Moreover, the molecules of a gas remain evenly distributed throughout the entire volume of a glass bulb and never spontaneously assemble in only one portion of the available volume. To help explain why these phenomena proceed spontaneously in only one direction requires an additional state function called entropy (S), a thermodynamic property of all substances that is often described as the degree of "disorder". The identification of entropy with disorder is not incorrect, but it can sometimes be misleading. In chemistry, the degree of entropy in a system is better thought of as corresponding to the dispersal of kinetic energy among the particles in that system, or, in other words, the freedom of motion of the particles. In the following section we will explore this definition of entropy and describe it mathematically.
Entropy and Probability
A technical definition of entropy is a thermodynamic state function corresponding to the number of available microscopic states, or microstates, of a system. A microstate is any one possible distribution of energy among all the particles of a given system. In order to see how this concept of microstates relates to "disorder" and "energy dispersal", we can use the image of a deck of playing cards, as shown in Figure \(\PageIndex{2}\). In any new deck, the 52 cards are arranged by four suits, with each suit arranged in descending order − one particular order corresponding to one microstate. If the cards are shuffled, however, there are approximately 1068 different ways they might be arranged, which corresponds to 1068 different microscopic states. The entropy of an ordered new deck of cards is therefore low, whereas the entropy of a randomly shuffled deck is high. Another way to think of it is that entropy is a measure of the number of possibilities for the order of the deck.

Figure \(\PageIndex{2}\): Illustrating Low- and High-Entropy States with a Deck of Playing Cards. An new, unshuffled deck has only a single arrangement, so there is only one microstate. In contrast, a randomly shuffled deck can have any one of approximately 1068 different arrangements, which correspond to 1068 different microstates. Image used with permission (CC BY-3.0 ; Trainler).
In the same way, the greater the number of atoms or molecules in a chemical system, and the more freedom of motion they have, the more possibilities there will be for energy to be dispersed in different ways among the particles − a greater entropy. Consider a gas expanding into a vacuum. The entropy of the gas increases as it expands into a greater volume, since there are now more possible places for each particle to be. Adding more molecules of gas increases the number of microstates further and thus increases the entropy.
To see how entropy correlates with spontaneity, let's consider the possible arrangements of four gas molecules in a two-bulb container (Figure \(\PageIndex{3}\)). There are five possible arrangements: all four molecules in the left bulb (I); three molecules in the left bulb and one in the right bulb (II); two molecules in each bulb (III); one molecule in the left bulb and three molecules in the right bulb (IV); and four molecules in the right bulb (V). If we assign a different color to each molecule to keep track of it for this discussion (remember, however, that in reality the molecules are indistinguishable from one another), we can see that there are 16 different ways the four molecules can be distributed in the bulbs, each corresponding to a particular microstate. As shown in Figure \(\PageIndex{3}\), arrangement I is associated with a single microstate, as is arrangement V, so each arrangement has a probability of 1/16, not very likely. Arrangements II and IV each have a probability of 4/16 because each can exist in four microstates. Similarly, six different microstates can occur as arrangement III, making the probability of this arrangement 6/16. Notice that this arrangement has the largest number of possible microstates associated with it, and thus the highest entropy. Which arrangement would we expect to encounter? Clearly arrangement III, with half the gas molecules in each bulb, is the most probable arrangement. The others are not impossible but simply less likely. This simple example illustrates the fundamental principle that systems statistically favor situations of highest entropy.
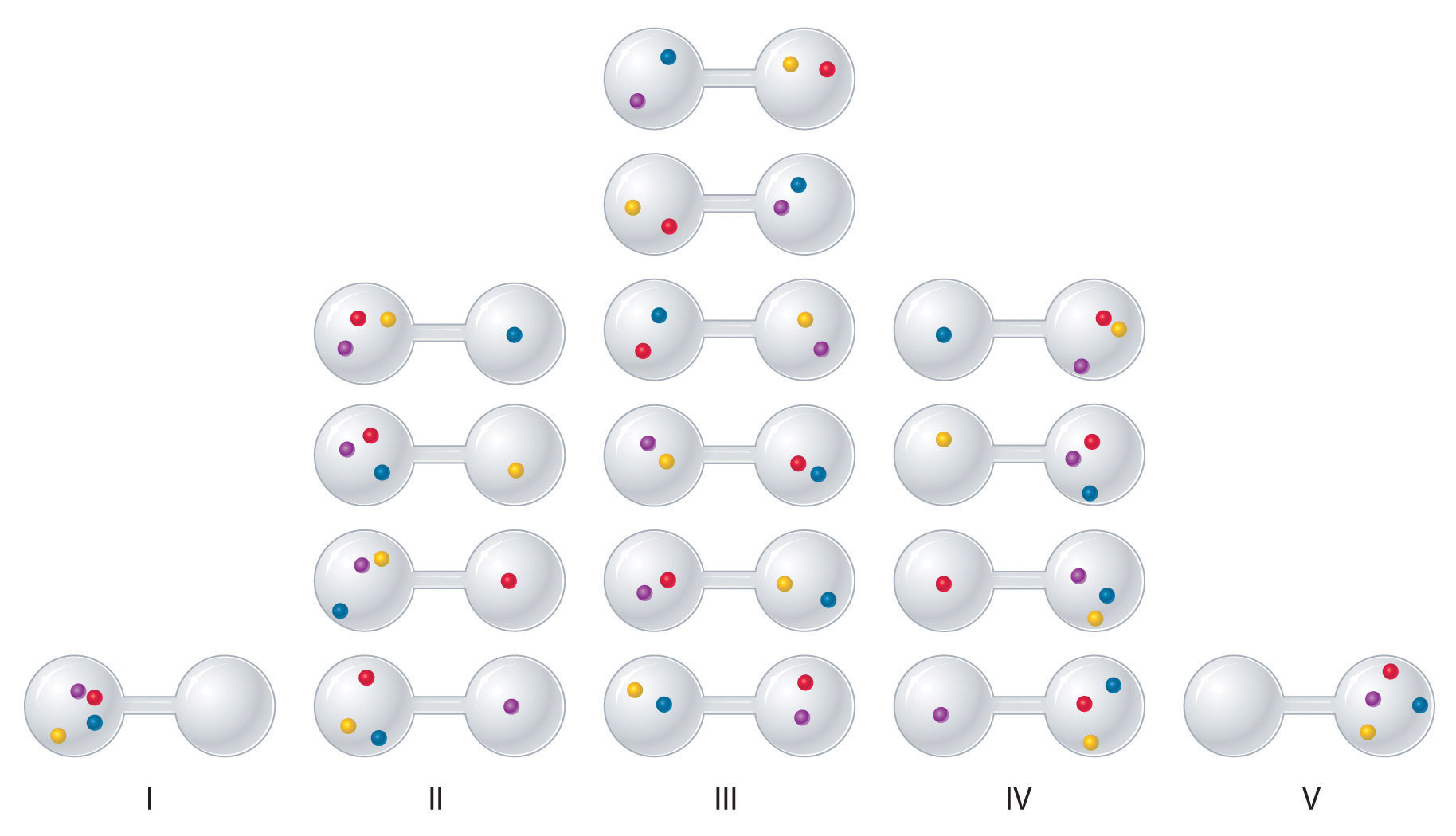
Figure \(\PageIndex{3}\): The Possible Microstates for a Sample of Four Gas Molecules in Two Bulbs of Equal Volume
Instead of four molecules of gas, what if we had one mole of gas, or 6.022 × 1023 molecules in the two-bulb apparatus? If we allow the sample of gas to expand spontaneously in the two containers, the probability of finding all 6.022 × 1023 molecules in one container and none in the other at any given time is extremely small, effectively zero. Although nothing prevents the molecules in the gas sample from occupying only one of the two bulbs, that particular arrangement is so improbable that it is never actually observed. The probability of arrangements with essentially equal numbers of molecules in each bulb is quite high, however, because there are many equivalent microstates in which the molecules are distributed equally. Hence a macroscopic sample of a gas occupies all of the space available to it, simply because this is the most probable arrangement.
Entropy depends not only on the number of atoms or molecules and the volume of available space, but also their freedom of motion, which corresponds to temperature and state of matter. Systems at a higher temperature, where molecules move faster on average, have a greater number of possible microstates for how the kinetic energy is distributed, so entropy increases with temperature. Entropy changes can also be clearly seen in transitions between phases of matter. As you know, a crystalline solid is composed of an ordered array of molecules, ions, or atoms that occupy fixed positions in a lattice, whereas the molecules in a liquid are free to move and tumble within the volume of the liquid; molecules in a gas have even more freedom to move than those in a liquid. Each degree of motion increases the number of available microstates, resulting in a higher entropy. Thus the entropy of a system must increase during melting (solid to liquid) or evaporation (liquid to gas). Conversely, the reverse processes (condensing a vapor to form a liquid or freezing a liquid to form a solid) must be accompanied by a decrease in the entropy of the system.
Another process that is accompanied by entropy changes is the formation of a solution. As illustrated in Figure \(\PageIndex{4}\), the formation of a liquid solution from a crystalline solid (the solute) and a liquid solvent is expected to result in an increase in the number of available microstates of the system and hence its entropy. Indeed, dissolving a substance such as NaCl in water disrupts both the ordered crystal lattice of NaCl and the ordered hydrogen-bonded structure of water, leading to an increase in the entropy of the system. At the same time, however, each dissolved Na+ ion becomes hydrated by an ordered arrangement of at least six water molecules, and the Cl− ions also cause the water to adopt a particular local structure, leading to an opposing decrease in entropy. The overall entropy change for the formation of a solution depends on the relative magnitudes of these opposing factors, but in general, as in the case of NaCl, the magnitude of the increase is greater than the magnitude of the decrease, so the overall entropy change for the formation of a solution is positive.
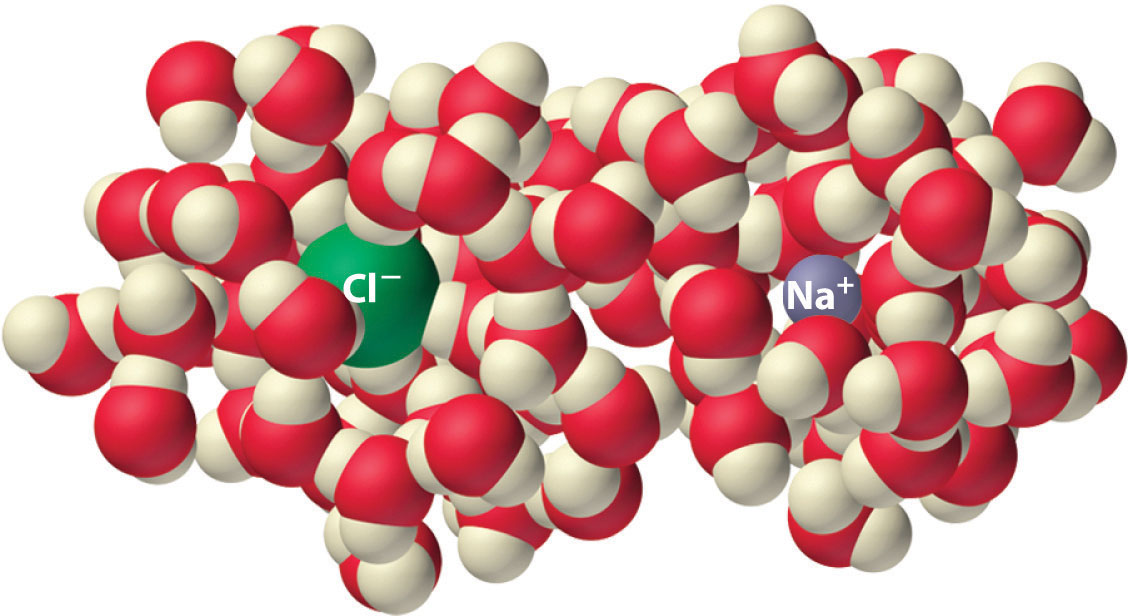
Figure \(\PageIndex{4}\): The Effect of Solution Formation on Entropy
Finally, entropy also increases with molecular size and complexity. A larger, more complicated molecule allows for more different ways that the atoms in that molecule can move relative to each other. This greater freedom of motion results in greater entropy. For example, liquid ethanol (CH3CH2OH) has a higher entropy than liquid water (H2O). It is important to note that this relationship only holds true if the two substances are in the same physical state − gaseous water would still have a higher entropy than liquid ethanol.
Example \(\PageIndex{1}\)
Predict which substance in each pair has the higher entropy and justify your answer.
- 1 mol of NH3(g) or 1 mol of He(g), both at 25°C
- 1 mol of Pb(s) at 25°C or 1 mol of Pb(l) at 800°C
Given: amounts of substances and temperature
Asked for: higher entropy
Strategy:
From the number of atoms present and the phase of each substance, predict which has the greater number of available microstates and hence the higher entropy.
Solution:
- Both substances are gases at 25°C, but one consists of He atoms and the other consists of NH3 molecules. With four atoms instead of one, the NH3 molecules have more motions available, leading to a greater number of microstates. Hence we predict that the NH3 sample will have the higher entropy.
- The nature of the atomic species is the same in both cases, but the phase is different: one sample is a solid, and one is a liquid. Based on the greater freedom of motion available to atoms in a liquid, we predict that the liquid sample will have the higher entropy.
Exercise \(\PageIndex{1}\)
Predict which substance in each pair has the higher entropy and justify your answer.
- 1 mol of He(g) at 10 K and 1 atm pressure or 1 mol of He(g) at 250°C and 0.2 atm
- a mixture of 3 mol of H2(g) and 1 mol of N2(g) at 25°C and 1 atm or a sample of 2 mol of NH3(g) at 25°C and 1 atm
- Answer a
-
1 mol of He(g) at 250°C and 0.2 atm (higher temperature and lower pressure indicate greater volume and more microstates)
- Answer a
-
a mixture of 3 mol of H2(g) and 1 mol of N2(g) at 25°C and 1 atm (more molecules of gas are present)
Entropy and the Second Law of Thermodynamics
Changes in entropy (ΔS), together with changes in enthalpy (ΔH), enable us to predict in which direction a chemical or physical change will occur spontaneously. Any chemical or physical change in a system may be accompanied by either an increase in entropy (ΔS > 0) or a decrease in entropy (ΔS < 0), respectively. As with any other state function, the change in entropy of a system is defined as the difference between the entropies of the final and initial states: ΔSsys = Sf − Si. The change in the system may also be accompanied by a change in entropy of the surroundings, ΔSsurr. However, unlike in the case of internal energy, entropy is not conserved − that is, ΔSsys and ΔSsurr may have different values. In fact, in all observable situations, the sum of ΔSsys and ΔSsurr is greater than or equal to zero. In other words, the entropy of the universe only ever increases or stays the same. This is one way of stating the second law of thermodynamics.
\[ \Delta S_{\textrm{univ}} = \Delta S_{\textrm{sys}}+\Delta S_{\textrm{surr}} \geq 0 \label{Eq1}\]
The second law offers the key to understanding spontaneity. A spontaneous process is one in which the entropy of the universe increases; while a nonspontaneous process would be one in which the entropy of the universe decreases (but this is never observed). In fact, the only way to make a "nonspontaneous" process occur is to drive it forward using another, spontaneous process, which would increase the entropy of the universe by more than the nonspontaneous process decreases entropy. Because the reverse of a spontaneous process would decrease the entropy of the universe, spontaneous processes are said to be irreversible.
The Second Law of Thermodynamics
The entropy of the universe increases during an irreversible (spontaneous or observable nonspontaneous) process, and remains constant during a reversible process.
The only situation where entropy of the universe remains constant is in a reversible process. In a thermodynamically reversible process, every intermediate state between the extremes is an equilibrium state. As a result, a reversible process can change direction at any time and is not spontaneous in one direction or another. When a gas expands reversibly against an external pressure such as a piston, for example, the expansion can be reversed at any time by reversing the motion of the piston; once the gas is compressed, it can be allowed to expand again, and the process can continue indefinitely. In contrast, the expansion of a gas into a vacuum (Pext = 0) is irreversible because the external pressure is measurably less than the internal pressure of the gas. No equilibrium states exist, and the gas expands irreversibly. When gas escapes from a microscopic hole in a balloon into a vacuum, for example, the process is irreversible; the direction of airflow cannot change. This distinction between reversible and irreversible changes will become important when we discuss the concept of chemical equilibrium in the second semester.
It would be difficult to measure entropy changes for the entire universe at once; therefore, we need to find a way to define entropy changes in terms of quantities we can easily measure, such as heat. For any process, we can determine the quantity of heat transferred between the system and the surroundings, q. In order to define entropy quantitatively, we need to consider the amount of heat transferred in the hypothetical situation where the change occurs reversibly, qrev. (This is necessary because q is not a state function, but entropy is; qrev is the minimum amount of heat that could be transferred in a process, regardless of the path taken.) Adding heat to a system increases the kinetic energy of the component atoms and molecules and hence their entropy (ΔS ∝ qrev). Moreover, because the quantity of heat transferred is directly proportional to the absolute temperature of an object (T) (qrev ∝ T), the hotter the object, the greater the amount of heat transferred. Combining these relationships for any reversible process,
Because the numerator (qrev) is expressed in units of energy (joules), the units of ΔS are joules/kelvin (J/K). Recognizing that the work done in a reversible process at constant pressure is wrev = −PΔV, we can also express the relationship between ΔS and ΔU as follows:
\[ \begin{align} ΔU &= q_{rev} + w_{rev} \\[5pt] &= TΔS − PΔV \label{Eq3} \end{align}\]
Thus the change in the internal energy of the system is related to the change in entropy, the absolute temperature, and the \(PV\) work done. In a process that occurs at constant pressure with little change in volume, such as a reaction involving only solids or liquids, ΔU depends only on qrev, which is therefore also equal to the enthalpy, ΔH. Therefore, changes in enthalpy can be used to approximate changes in entropy for both the system and the surroundings.
To illustrate this definition of entropy, consider the entropy changes that accompany the spontaneous and irreversible transfer of heat from a hot object to a cold one, as occurs when lava spewed from a volcano flows into cold ocean water. The cold substance, the water, gains heat (q > 0), so the change in the entropy of the water can be written as ΔScold = q/Tcold. Similarly, the hot substance, the lava, loses heat (q < 0), so its entropy change can be written as ΔShot = −q/Thot, where Tcold and Thot are the temperatures of the cold and hot substances, respectively. The total entropy change of the universe accompanying this process is therefore
The numerators on the right side of Equation \(\ref{Eq4}\) are the same in magnitude but opposite in sign. Whether ΔSuniv is positive or negative depends on the relative magnitudes of the denominators. By definition, Thot > Tcold, so −q/Thot must be less than q/Tcold, and ΔSuniv must be positive. As predicted by the second law of thermodynamics, the entropy of the universe increases during this irreversible process. Any process for which ΔSuniv is positive is, by definition, a spontaneous one that will occur as written. Conversely, any process for which ΔSuniv is negative will not occur as written but will occur spontaneously in the reverse direction. We see, therefore, that heat is spontaneously transferred from a hot substance, the lava, to a cold substance, the ocean water. In fact, if the lava is hot enough (e.g., if it is molten), so much heat can be transferred that the water is converted to steam (Figure \(\PageIndex{5}\)).

Figure \(\PageIndex{5}\): Spontaneous Transfer of Heat from a Hot Substance to a Cold Substance
Example \(\PageIndex{2}\): Tin Pest
Tin has two allotropes with different structures. Gray tin (α-tin) has a structure similar to that of diamond, whereas white tin (β-tin) is denser, with a unit cell structure that is based on a rectangular prism. At temperatures greater than 13.2°C, white tin is the more stable phase, but below that temperature, it slowly converts reversibly to the less dense, powdery gray phase. This phenomenon can degrade objects made out of tin (such as cans, utensils, or pipes) if exposed to very cold temperatures for long periods of time. The conversion of white tin to gray tin is exothermic, with ΔH = −2.1 kJ/mol at 13.2°C.
- What is ΔS for this process?
- Which is the more highly ordered form of tin—white or gray?
Given: ΔH and temperature
Asked for: ΔS and relative degree of order
Strategy:
Use Equation \(\ref{Eq2}\) to calculate the change in entropy for the reversible phase transition. From the calculated value of ΔS, predict which allotrope has the more highly ordered structure.
Solution:
- We know from Equation \(\ref{Eq2}\) that the entropy change for any reversible process is the heat transferred (in joules) divided by the temperature at which the process occurs. Because the conversion occurs at constant pressure, and ΔH and ΔU are essentially equal for reactions that involve only solids, we can calculate the change in entropy for the reversible phase transition where qrev = ΔH. Substituting the given values for ΔH and temperature in kelvins (in this case, T = 13.2°C = 286.4 K),
- The fact that ΔS < 0 means that entropy decreases when white tin is converted to gray tin. Thus gray tin must be the more highly ordered structure.
Exercise \(\PageIndex{2}\)
Elemental sulfur exists in two forms: an orthorhombic form (Sα), which is stable below 95.3°C, and a monoclinic form (Sβ), which is stable above 95.3°C. The conversion of orthorhombic sulfur to monoclinic sulfur is endothermic, with ΔH = 0.401 kJ/mol at 1 atm.
- What is ΔS for this process?
- Which is the more highly ordered form of sulfur—Sα or Sβ?
- Answer a
-
1.09 J/(mol•K)
- Answer b
-
Sα
Standard Molar Entropy, S0
We have seen that the energy given off (or absorbed) by a reaction, and monitored by noting the change in temperature of the surroundings, can be used to determine the enthalpy of a reaction (e.g. by using a calorimeter). Unfortunately, there is not always an easy way to measure the change in entropy for a reaction experimentally . Suppose we know that energy is going into a system (or coming out of it), and yet we do not observe any change in temperature. What is going on in such a situation? Changes in internal energy, that are not accompanied by a temperature change, might reflect changes in the entropy of the system.
For example, consider water at °0 C at 1 atm pressure. This is the temperature and pressure condition where liquid and solid phases of water are in equilibrium (also known as the melting point of ice)
\[\ce{H2O(s) \rightarrow H2O(l)} \]
At such a temperature and pressure we have a situation (by definition) where we have some ice and some liquid water. If a small amount of energy is input into the system the equilibrium will shift slightly to the right (i.e. in favor of the liquid state). Likewise if a small amount of energy is withdrawn from the system, the equilibrium will shift to the left (more ice). However, in both of these situations, the energy change is not accompanied by a change in temperature (the temperature will not change until we no longer have an equilibrium condition; i.e. all the ice has melted or all the liquid has frozen)
Since the quantitative term that relates the amount of heat energy input vs. the rise in temperature is the heat capacity, it would seem that in some way, information about the heat capacity (and how it changes with temperature) would allow us to determine the entropy change in a system. In fact, values for the "standard molar entropy" of a substance have units of J/mol K, the same units as for molar heat capacity.
The same hardworking physical chemists who gave us standard enthalpies of formation have also constructed tables of standard molar entropy, S0, for a wide variety of substances under standard conditions. Standard molar entropy values are listed for a variety of substances in Table T2. These tabulated values allow us to calculate the entropy changes in various chemical reactions.
Rules about standard molar entropies:
- Remember that the entropy of a substance increases with temperature. The entropy of a substance has an absolute value of 0 entropy at 0 K. (This, by the way, is a statement of the third law of thermodynamics.)
- Standard molar entropies are listed for a reference temperature (like 298 K) and 1 atm pressure (i.e. the entropy of a pure substance at 298 K and 1 atm pressure). A table of standard molar entropies at 0 K would be pretty useless because it would be 0 for every substance (duh!)
- When comparing standard molar entropies for a substance that is either a solid, liquid or gas at 298 K and 1 atm pressure, the gas will have more entropy than the liquid, and the liquid will have more entropy than the solid
- Unlike enthalpies of formation, standard molar entropies of elements are not 0.
The entropy change in a chemical reaction is given by the sum of the entropies of the products minus the sum of the entropies of the reactants. As with other calculations related to balanced equations, the coefficients of each component must be taken into account in the entropy calculation (the n, and m, terms below are there to indicate that the coefficients must be accounted for):
\[ \Delta S^0 = \sum_n nS^0(products) - \sum_m mS^0(reactants)\]
Example \(\PageIndex{3}\): Haber Process
Calculate the change in entropy associated with the Haber process for the production of ammonia from nitrogen and hydrogen gas.
\[\ce{N2(g) + 3H2(g) \rightleftharpoons 2NH3(g)} \nonumber \]
At 298K as a standard temperature:
- S0(NH3) = 192.5 J/mol K
- S0(H2) = 130.6 J/mol K
- S0(N2) = 191.5 J/mol K
Solution
From the balanced equation we can write the equation for ΔS0 (the change in the standard molar entropy for the reaction):
ΔS0 = 2*S0(NH3) - [S0(N2) + (3*S0(H2))]
ΔS0 = 2*192.5 - [191.5 + (3*130.6)]
ΔS0 = -198.3 J/mol K
It would appear that the process results in a decrease in entropy - i.e. a decrease in disorder. This is expected because we are decreasing the number of gas molecules. In other words the N2(g) used to float around independently of the H2 gas molecules. After the reaction, the two are bonded together and can't float around freely from one another. This decreases the overall freedom of motion of the particles involved and therefore their entropy.
To calculate ΔS° for a chemical reaction from standard molar entropies, we use the familiar “products minus reactants” rule, in which the absolute entropy of each reactant and product is multiplied by its stoichiometric coefficient in the balanced chemical equation. Example \(\PageIndex{4}\) illustrates this procedure for the combustion of the liquid hydrocarbon isooctane (C8H18; 2,2,4-trimethylpentane).
ΔS° for a reaction can be calculated from absolute entropy values using the same “products minus reactants” rule used to calculate ΔH°.
Example \(\PageIndex{4}\): Combustion of Octane
Use the data in Table T2 to calculate ΔS° for the combustion reaction of liquid isooctane with O2(g) to give CO2(g) and H2O(g) at 298 K.
Given: standard molar entropies, reactants, and products
Asked for: ΔS°
Strategy:
Write the balanced chemical equation for the reaction and identify the appropriate quantities in Table T2. Subtract the sum of the absolute entropies of the reactants from the sum of the absolute entropies of the products, each multiplied by their appropriate stoichiometric coefficients, to obtain ΔS° for the reaction.
Solution:
The balanced chemical equation for the complete combustion of isooctane (C8H18) is as follows:
We calculate ΔS° for the reaction using the “products minus reactants” rule, where m and n are the stoichiometric coefficients of each product and each reactant:
\begin{align*}\Delta S^\circ_{\textrm{rxn}}&=\sum mS^\circ(\textrm{products})-\sum nS^\circ(\textrm{reactants})
\\ &=[8S^\circ(\mathrm{CO_2})+9S^\circ(\mathrm{H_2O})]-[S^\circ(\mathrm{C_8H_{18}})+\dfrac{25}{2}S^\circ(\mathrm{O_2})]
\\ &=\left \{ [8\textrm{ mol }\mathrm{CO_2}\times213.8\;\mathrm{J/(mol\cdot K)}]+[9\textrm{ mol }\mathrm{H_2O}\times188.8\;\mathrm{J/(mol\cdot K)}] \right \}
\\ &-\left \{[1\textrm{ mol }\mathrm{C_8H_{18}}\times329.3\;\mathrm{J/(mol\cdot K)}]+\left [\dfrac{25}{2}\textrm{ mol }\mathrm{O_2}\times205.2\textrm{ J}/(\mathrm{mol\cdot K})\right ] \right \} \\ &=515.3\;\mathrm{J/K}\end{align*}
ΔS° is positive, as expected for a combustion reaction in which one large hydrocarbon molecule is converted to many molecules of gaseous products.
Exercise \(\PageIndex{4}\)
Use the data in Table T2 to calculate ΔS° for the reaction of H2(g) with liquid benzene (C6H6) to give cyclohexane (C6H12).
- Answer
-
−361.1 J/K
Summary
A measure of the disorder of a system is its entropy (S), a state function whose value increases with an increase in the number of available microstates. For a given system, the greater the number of microstates, the higher the entropy. The second law of thermodynamics states that in a reversible process, the entropy of the universe is constant, whereas in an irreversible process, such as the transfer of heat from a hot object to a cold object, the entropy of the universe increases. During a spontaneous process, the entropy of the universe increases. Entropy changes in chemical reactions can be calculated using standard molar entropies in a way analogous to calculating enthalpy changes.

