24.5 Biological Amines and the Henderson-Hasselbalch Equation
- Page ID
- 91033
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Objectives
- identify the form that amine bases take within living cells.
- use the Henderson‑Hasselbalch equation to calculate the percentage of a base that is protonated in a solution, given the pKa value of the associated ion and the pH of the solution.
- explain why organic chemists write cellular amines in their protonated form and amino acids in their ammonium carboxylate form.
The Henderson-Hasselbalch equation is a very useful equation relating the pKa of a buffered solution to the relative amounts of an acid and its conjugate base.
The Henderson-Hasselbalch equation:
![pH = pKₐ + log([A⁻]/[HA])](https://chem.libretexts.org/@api/deki/files/388041/Henderson-Hasselbalch.png?revision=1&size=bestfit&width=266&height=63)
If an acid is exactly 50% dissociated in aqueous solution, then the concentration of A- is equal to the concentration of HA, and the fraction term in the Henderson-Hasselbalch equation is equal to 1. Because log(1) = 0, it follows that pH = pKa at these conditions. This is very useful: it means that the pKa of an acid is equal to the pH at which it is 50% disassociated (deprotonated). For example, if a 0.1 M aqueous solution of acetic acid is brought to pH 4.8 by the addition of sodium hydroxide, we know by the Henderson-Hasselbalch equation that the solution is now 0.05 M in acetic acid and 0.05 M in acetate ion.
The above situation – an aqueous solution that contains equal or nearly equal concentrations of a weak acid and its conjugate base – should sound very familiar to you. This is a buffer! As we discuss the organic reactions that occur in living things, it will be very important to always keep in mind that most of these reactions are occurring in an aqueous solution that is buffered to approximately pH 7.3 (the exceptions are reactions occuring in lysosomes and endosomes, specialized organelles in eukaryotic cells that maintain a slightly acidic interior). The buffer in a living cell is not composed of acetic acid/acetate mixture, or course – that would make the pH far too acidic. Rather, the chemistry of life occurs in a buffer that consists of a mixture of various phosphate and ammonium compounds.
So, what does the side chain of an aspartate amino acid residue look like if it is on the surface of a protein in an aqueous solution buffered to pH 7.0? Is it protonated or deprotonated? With an approximate pKa of 3.9, the Henderson-Hasselbalch equation tells us that the side chain should be greater than 99% deprotonated:
7.0 = 3.9 + log ([A-] / [HA])
([A-] / [HA]) = 1.3 x 103
. . . so, [A-] >> [HA]
What about the amino group on a lysine side chain? With an approximate pKa of 10.8, it should be >99% protonated, in the positively-charged, ammonium form:
7.0 = 10.8 + log ([A] / [HA+])
([A] / [HA+]) = 1.6 x 10-4
. . . so, [HA+] >> [A]
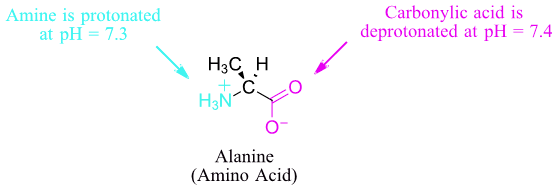
So, in an aqueous solution buffered at pH 7, carboxylic acid groups can be expected to be essentially 100% deprotonated and negatively charged (ie. in the carboxylate form), and amine groups essentially 100% protonated and positively charged (i.e., in the ammonium form). Alcohols are fully protonated and neutral at pH 7, as are thiols. The imidizole group on the histidine side chain has a pKa near 7, and thus exists in physiological solutions as mixture of both protonated and deprotonated forms.
Exercise
Would you expect an aromatic hetererocycle, pyrrole, to be protonated at pH = 7.3? Use the Henderson-Hasselbalch equation to determine your answer. pKa of protonated pyrrole is 0.4.
- Answer
-
7.3 = 0.4 + log ([RNH2] / [RNH3+])
([RNH2] / [RNH3+]) = 7.9 x 106
. . . so, [RNH2] >> [RNH3+] so pyrrole would be almost completely unprotonated at pH = 7.
Contributors and Attributions
Dr. Dietmar Kennepohl FCIC (Professor of Chemistry, Athabasca University)
Prof. Steven Farmer (Sonoma State University)
William Reusch, Professor Emeritus (Michigan State U.), Virtual Textbook of Organic Chemistry
Organic Chemistry With a Biological Emphasis by Tim Soderberg (University of Minnesota, Morris)

