5.7: Meso Compounds
- Page ID
- 67099
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)After completing this section, you should be able to
- determine whether or not a compound containing two chiral carbon atoms will have a meso form, given its Kekulé, condensed or shorthand structure, or its IUPAC name.
- draw wedge-and-broken-line structures for the enantiomers and meso form of a compound such as tartaric acid, given its IUPAC name, or its Kekulé, condensed or shorthand structure.
- make a general comparison of the physical properties of the enantiomers, meso form and racemic mixture of a compound such as tartaric acid.
Make certain that you can define, and use in context, the key term below.
- meso compound
You may be confused by the two sets of structures showing “rotations.” Of course in each case the two structures shown are identical, they represent the same molecule looked at from two different perspectives. In the first case, there is a 120° rotation around the single carbon-carbon bond. In the second, the whole molecule is rotated 180° top to bottom.
Meso Compounds
A meso compound is an achiral compound that has chiral centers. It is superimposed on its mirror image and is optically inactive although it contains two or more stereocenters.
Introduction
In general, a meso compound should contain two or more identical substituted stereocenters. Also, it has an internal symmetry plane that divides the compound in half. These two halves reflect each other by the internal mirror. The stereochemistry of stereocenters should "cancel out". What it means here is that when we have an internal plane that splits the compound into two symmetrical sides, the stereochemistry of both left and right side should be opposite to each other, and therefore, result in optically inactive. Cyclic compounds may also be meso.
Identification
If A is a meso compound, it should have two or more stereocenters, an internal plane, and the stereochemistry should be R and S.
- Look for an internal plane, or internal mirror, that lies in between the compound.
- The stereochemistry (e.g. R or S) is very crucial in determining whether it is a meso compound or not. As mentioned above, a meso compound is optically inactive, so their stereochemistry should cancel out. For instance, R cancels S out in a meso compound with two stereocenters.
.bmp?revision=1&size=bestfit&width=375&height=171)
trans-1,2-dichloro-1,2-ethanediol
.bmp?revision=1&size=bestfit&width=433&height=183)
(meso)-2,3-dibromobutane
Tips: An interesting thing about single bonds or sp3-orbitals is that we can rotate the substituted groups that attached to a stereocenter around to recognize the internal plane. As the molecule is rotated, its stereochemistry does not change. For example:
.bmp?revision=1&size=bestfit&width=412&height=258)
Another case is when we rotate the whole molecule by 180 degree. Both molecules below are still meso.
Remember the internal plane here is depicted on two dimensions. However, in reality, it is three dimensions, so be aware of it when we identify the internal mirror.
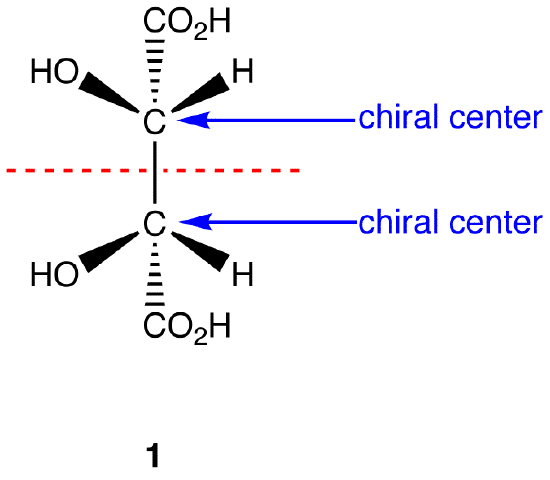
1 has a plane of symmetry (the horizonatal plane going through the red broken line) and, therefore, is achiral; 1 has chiral centers. Thus, 1 is a meso compound.
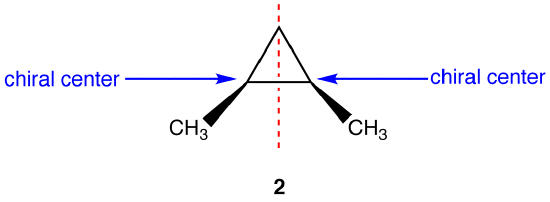
This molecules has a plane of symmetry (the vertical plane going through the red broken line perpendicular to the plane of the ring) and, therefore, is achiral, but has has two chiral centers. Thus, its is a meso compound.
Other Examples of meso compounds
Meso compounds can exist in many different forms such as pentane, butane, heptane, and even cyclobutane. They do not necessarily have to be two stereocenters, but can have more.
.bmp?revision=1&size=bestfit&width=695&height=176)
Optical Activity Analysis
When the optical activity of a meso compound is attempted to be determined with a polarimeter, the indicator will not show (+) or (-). It simply means there is no certain direction of rotation of the polarized light, neither levorotatory (-) and dexorotatory (+).
Achiral Diastereomers (meso-Compounds)
The chiral centers in the preceding examples have all been different. In the case of 2,3-dihydroxybutanedioic acid, known as tartaric acid, the two chiral centers have the same four substituents and are equivalent. As a result, two of the four possible stereoisomers of this compound are identical due to a plane of symmetry, so there are only three stereoisomeric tartaric acids. Two of these stereoisomers are enantiomers and the third is an achiral diastereomer, called a meso compound. Meso compounds are achiral (optically inactive) diastereomers of chiral stereoisomers. Investigations of isomeric tartaric acid salts, carried out by Louis Pasteur in the mid 19th century, were instrumental in elucidating some of the subtleties of stereochemistry. Some physical properties of the isomers of tartaric acid are given in the following table.
| (+)-tartaric acid: | [α]D = +13º | m.p. 172 ºC |
| (–)-tartaric acid: | [α]D = –13º | m.p. 172 ºC |
| meso-tartaric acid: | [α]D = 0º | m.p. 140 ºC |
Fischer projection formulas provide a helpful view of the configurational relationships within the structures of these isomers. In the following illustration a mirror line is drawn between formulas that have a mirror-image relationship. In demonstrating the identity of the two meso-compound formulas, remember that a Fischer projection formula may be rotated 180º in the plane.
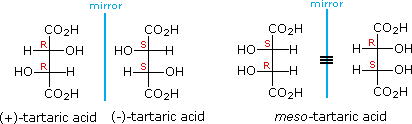
Problems
Beside meso, there are also other types of molecules: enantiomer, diastereomer, and identical. Determine if the following molecules are meso.
Answer key: A C, D, E are meso compounds.
Exercises
Which of the following are meso compounds?
- Answer
-
a) This is a meso compound. There is an internal plane of symmetry (dashed line shown in red) between the C’s (and it has stereochemistry of S & R).
b) This is not a meso compound. No matter how you rotate the C-C bond, you do not see a plane of symmetry (and its stereochemistry is S & S)
c) This is a meso compound. There is an internal plane of symmetry (dashed line shown in red) that can be seen when you rotate the C-C bond (and it has stereochemistry of S & R).
Which of the following are meso compounds?
- Answer
-
a) This is not a meso compound. There is no plane of symmetry and has stereochemistry of S & S.
b) This is a meso compound. There is an internal plane of symmetry (dashed line shown in red) and it has stereochemistry of R & S.
c) This is not a meso compound (even though it has planes of symmetry). The plane of symmetry shown in red makes it so that both chiral centers have symmetrical groups (the ring) and thus the compound is not chiral (so it can’t be a meso compound).
Which of the following are meso compounds?
- Answer
-
a) This is a meso compound. If you rotate between the C-C bond, you can see that it has a mirror plane between the C’s (shown in red on the structure to the right). Notice how rotating a C-C bond doesn’t change the stereochemistry of the molecule (S & R).
b) This is a meso compound. You can see the plane of symmetry in red and the compound has stereochemistry of S & R.
c) This is not a meso compound. There is no plane of symmetry and it has stereochemistry of S & S.
Determine (and draw) if any of the forms of 3,4-dichlorohexane are a meso compound.
- Answer
-
Looking at the 4 different possibilities below, i & ii are equivalent structures (with R & S stereochemistry) so it is a meso compound. iii & iv are not meso compounds but are enantiomers to each other.
Contributors and Attributions
- Duy Dang
- Gamini Gunawardena from the OChemPal site (Utah Valley University)
William Reusch, Professor Emeritus (Michigan State U.), Virtual Textbook of Organic Chemistry
Dr. Dietmar Kennepohl FCIC (Professor of Chemistry, Athabasca University)

