15.7: An Introduction to pH

⚙️ Learning Objectives

• Define pH and acidic, basic, and neutral pH values.
• Determine the magnitude of change in [H₃O⁺] for changing pH values.

Perhaps you have heard of the term pH used to describe the acidity or basicity of a substance or you already know that a pH = 7 is neutral – neither acidic, nor basic. What is the pH and what does it mean? If a carbonated beverage has a pH = 3, how does it compare to a solution that has a pH = 6? Is it half as acidic? Twice as acidic? Or is it something entirely different? (Hint: It is!)
 

Figure \(\PageIndex{1}\): A typical cola has a pH ≤ 3. (rawpixel via FreeRange)

The pH Scale

We have seen that \(\left[{\mathrm H}_3\mathrm O^+\right]\) and \(\left[\mathrm{OH}^-\right]\) values may be very small and vary widely from one solution to another. Before it was known that H⁺ ions were unlikely to exist in aqueous solution, Danish scientist Søren Sørensen (1868-1939) proposed a system for representing the \(\left[\mathrm H^+\right]\) called the pH scale. The letters pH stand for the "power of the hydrogen ion" and was originally defined as the negative logarithm of the hydrogen ion concentration, as shown in Equation \(\PageIndex{1}\) (read about Logarithmic Scales below):

\[\mathrm{pH}=-\log\left[\mathrm H^+\right]\]

Today, we know that acids produce hydronium ions in solution rather than hydrogen ions, so the definition of pH may be slightly reworded to be the negative logarithm of the hydronium ion concentration:

\[\mathrm{pH}=-\log\left[{\mathrm H}_3\mathrm O^+\right]\]

In pure water, we have already established that \(\left[{\mathrm H}_3\mathrm O^+\right]=\left[\mathrm{OH}^-\right]=10^{-7}\;\mathrm M\). Substituting \(\left[{\mathrm H}_3\mathrm O^+\right]=10^{-7}\;\mathrm M\) into the equation, \(\mathrm{pH}=-\log\left[{\mathrm H}_3\mathrm O^+\right]\):

\(\mathrm{pH}=-\log\left[10^{-7}\right]=-\left(-7\right)=7\)

Thus, the pH = 7 for pure water (or any neutral solution). It should also be noted that pH values have no units. The pH of pure water is simply 7.
 

⛓ Logarithmic Scales

What is a logarithm and why is it used to represent the acidity or basicity of a solution? The \(\left[{\mathrm H}_3\mathrm O^+\right]\) of an aqueous solution is almost always in the range of 10^–14 M to 1 M. This is an extremely wide range that is over several orders of magnitude. A logarithmic scale condenses this range of values to numbers that are easier to use, almost always in the range of 0 to 14.

Logarithms have different "bases". Base-10 logarithms, which are based on magnitudes of 10, are used to calculate pH. Some example logarithm calculations:

\(\log\left(10^5\right)=5\)

\(\log\left(10^{-9}\right)=-9\)

Therefore, in general:

\(\log\left(10^x\right)=x\)

Each integer value increment represents a factor of 10. In the case of the pH, we define it as being the negative logarithm of the hydronium ion concentration, \(\mathrm{pH}=-\log\left[{\mathrm H}_3\mathrm O^+\right]\). Therefore, a solution with a pH = 3 has a \(\left[{\mathrm H}_3\mathrm O^+\right]\) = 10^–3 M, which is 10 times larger than a solution with a pH = 4, which has a \(\left[{\mathrm H}_3\mathrm O^+\right]\) = 10^–4 M, and a solution with a pH = 4 has a \(\left[{\mathrm H}_3\mathrm O^+\right]\) that is 10 times larger than a solution with a pH = 5, which has a \(\left[{\mathrm H}_3\mathrm O^+\right]\) = 10^–5 M. This means that a solution with a pH = 3 has a \(\left[{\mathrm H}_3\mathrm O^+\right]\) that is 100 times larger than a solution with a pH = 5. In other words, each whole number decrease in pH value represents a 10-fold increase in the \(\left[{\mathrm H}_3\mathrm O^+\right]\).

To answer the question asked at the beginning of this section, "If a carbonated beverage has a pH = 3, how does it compare to a solution that has a pH = 6?" We can now say that a solution with a pH = 3 is 10×10×10, or 10³ times the acidity of a solution with a pH = 6, in terms of the \(\left[{\mathrm H}_3\mathrm O^+\right]\); not twice as acidic or half as acidic.
 

Figure \(\PageIndex{2}\): Earthquake damage in Portsmouth, Dominica from magnitude 6.2 Les Saintes earthquake. (21 November, 2004). (UWI Seismic Research Centre via Flickr)

Other measurements based on a logarithmic scale include the Richter scale, used to measure earthquake intensity and sound intensity, which is measured in units called decibels (dB). In the case of the Richter scale, each whole number increment in magnitude represents a 10-fold increase in earthquake intensity. An earthquake with a magnitude of 7.2 has 10 times the intensity of an earthquake with a magnitude of 6.2, which has 10 times the intensity of an earthquake with a magnitude of 5.2. This means that an earthquake with a magnitude of 7.2 has 100 times the intensity of an earthquake with a magnitude of 5.2.

In the case of sound intensity, each decibel (dB) represents ⅒ bel (B). This means that each increment of 10 dB represents a 10-fold increase in sound intensity. A sound intensity level of 98 dB has 10 times the intensity of 88 dB, which has 10 times the intensity of 78 dB. In other words, a sound intensity level of 98 dB has 100 times the intensity of 78 dB. 

As established in the previous section, a solution with a \(\left[{\mathrm H}_3\mathrm O^+\right]\) greater than \(1.0\times10^{-7}\;\mathrm M\) is acidic, while a solution with a \(\left[{\mathrm H}_3\mathrm O^+\right]\) less than \(1.0\times10^{-7}\;\mathrm M\) is basic. In terms of pH, this may be summarized as follows:

• If pH < 7, then the solution is acidic.
• If pH = 7, then the solution is neutral.
• If pH > 7, then the solution is basic.

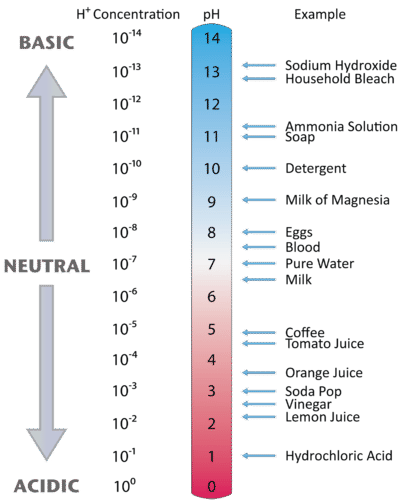
Figure \(\PageIndex{3}\) shows the pH scale in relation to several common materials (the H⁺ concentration in the figure below is the same as the \(\left[{\mathrm H}_3\mathrm O^+\right]\)).
 

Figure \(\PageIndex{3}\): The pH values for several common materials.

 

✅ Example \(\PageIndex{1}\)

Identify each solution as acidic, basic, or neutral.

1. milk of magnesia, pH = 10.5
2. a salt solution, pH = 7
3. wine, pH = 3.0

Solution

1. With a pH >7, milk of magnesia is basic. [Note: Milk of magnesia is the common name for Mg(OH)₂.]
2. With a pH = 7, a salt solution is neutral.
3. With a pH < 7, wine is acidic.

 

✏️ Exercise \(\PageIndex{1}\)

Identify each substance as acidic, basic, or neutral.

1. Human blood with a pH = 7.4
2. Household ammonia with a pH = 11.0
3. Cherries with a pH = 3.6

Answer A

basic

Answer B

basic

Answer C

acidic

 

     

---

This page is shared under CK-12 and CC BY-NC-SA 4.0 licenses and was authored, remixed, and/or curated by Lance S. Lund (Anoka-Ramsey Community College), Peggy Lawson (Oxbow Prairie Heights School, funded by Saskatchewan Educational Technology Consortium), Marisa Alviar-Agnew, and Henry Agnew. Original sources: https://www.ck12.org/c/chemistry/ and https://openstax.org/details/books/chemistry-2e.

LICENSED UNDER