9.4: Pressure and Volume
- Page ID
- 289438
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)⚙️ Learning Objectives
- Learn what is meant by the term gas laws.
- Learn and apply Boyle’s Law.
When seventeenth-century scientists began studying the physical properties of gases, they noticed some simple relationships between some of the measurable properties of the gas. Consider the relationship between pressure (P) and volume (V), as shown in Figure \(\PageIndex{1}\).
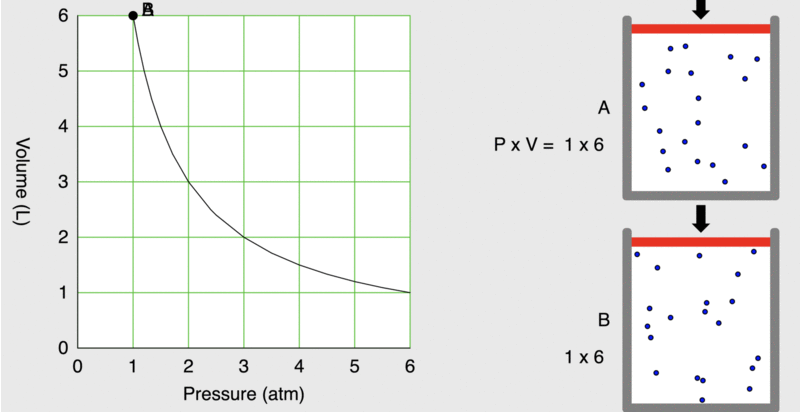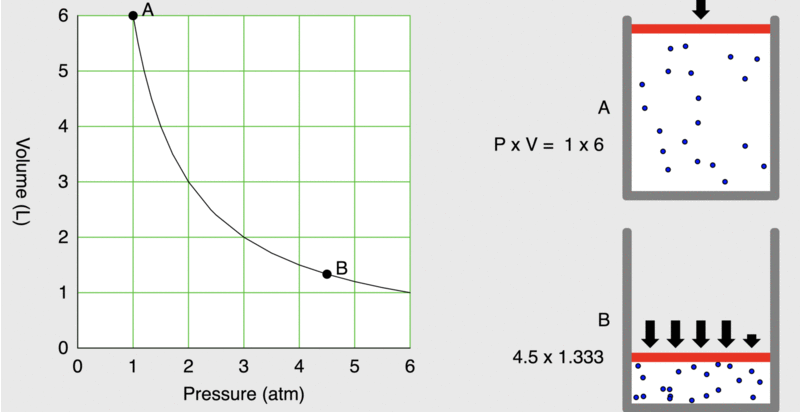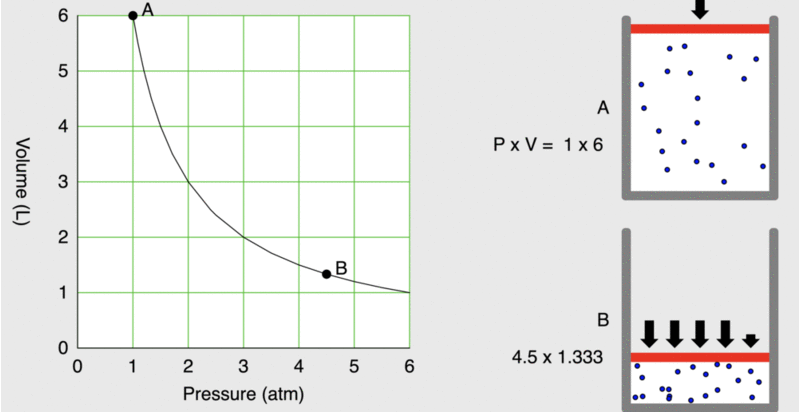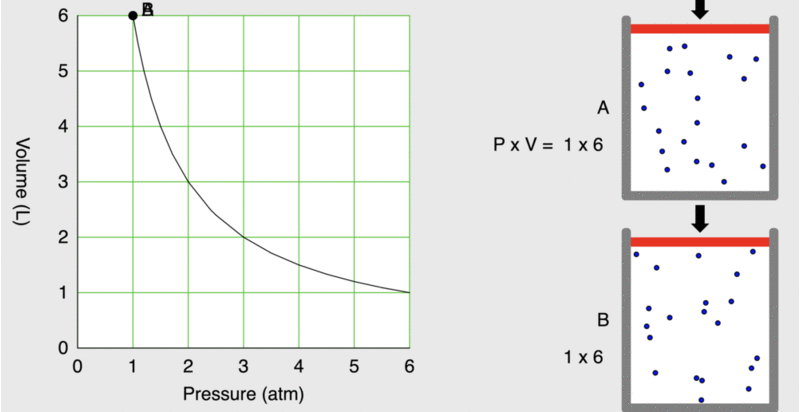
Figure \(\PageIndex{1}\): As the pressure on a piston increases, the volume inside the piston decreases. Note that the product, P×V, remains constant.
Boyle's Law
Assuming that the amount of a gas and the temperature (T) of the gas were kept constant, scientists found that pressure and volume were inversely proportional, i.e. as one increased, the other decreased in a proportionate manner. Or, as one decreased, the other increased in a proportionate manner.
This means that when two variables are inversely proportional, doubling one variable causes the other to be cut in half. Reducing one variable to ⅕ of its original value will cause the other variable to increase by a factor of 5. As a result, the product of the two variables remains constant. In the case of pressure and volume,
\[P\times V=\mathrm{constant}\]
Once again, this is for a given amount of gas at a constant temperature. If either volume or pressure changes while amount and temperature stay the same, then the other property must change so that the product of the two properties still equals that same constant. That is, if the original conditions are labeled \(P_1\) and \(V_1\) and the new conditions are labeled \(P_2\) and \(V_2\), we obtain
Equation \(\PageIndex{2}\) is an example of a gas law. A gas law is a simple mathematical formula that allows you to model, or predict, the behavior of a gas. This particular gas law is called Boyle's Law, after the English scientist Robert Boyle, who first announced it in 1662.
Tactics for working with mathematical formulas are different from tactics for working with conversion factors.
- First, most of the questions you will have to answer using formulas are word-type questions, so the first step is to identify what quantities are known and assign them to variables.
- Second, in most formulas, some mathematical rearrangements that require basic algebra must be performed to solve for an unknown variable. The rule is that to find the value of the unknown variable, you must mathematically isolate the unknown variable by itself and in the numerator of one side of the equation.
- Finally, units must be consistent. For example, in Boyle’s Law there are two pressure variables; they must have the same unit. There are also two volume variables; they also must have the same units. In most cases, it won’t matter what the unit is, but the unit must be the same on both sides of the equation.
✅ Example \(\PageIndex{1}\)
4.01 L of nitrogen gas has an initial pressure of 2.44 atm. What is the volume of the gas if the pressure changes to 1.93 atm? Assume a constant temperature.
Solution
| Steps for Problem Solving | |
|---|---|
Identify the "given" information and what the problem is asking you to "find." |
Given: P1 = 2.44 atm, V1 = 4.01 L, P2 = 1.93 atm Find: V2 = ? L |
List other known quantities. |
none |
Plan the problem. |
Rearrange the equation to solve for \(V_2\). \(V_2 = \dfrac{P_1 \times V_1}{P_2}\) |
| Calculate and cancel units. | Substitute the given quantities into the equation and solve. \(V_{\mathit2}=\dfrac{2.44\:\cancel{\mathrm{atm}}\times4.01\;\mathrm L}{1.93\;\cancel{\mathrm{atm}}}=5.07\;\mathrm L\) |
| Think about your result. | Pressure and volume are inversely proportional. The pressure decreased from 2.44 atm to 1.93 atm, so volume should increase to compensate, which it did (from 4.01 L to 5.07 L). |
✅ Example \(\PageIndex{2}\):
An 88.8 mL sample of carbon dioxide has an initial pressure of 722 mm Hg. What is the pressure of the gas if its volume changes to 0.663 L.
Solution
| Steps for Problem Solving | |
|---|---|
Identify the "given" information and what the problem is asking you to "find." |
Given: P1 = 722 mm Hg, V1 = 88.8 mL, V2 = 0.633 L Find: P2 = ? mm Hg |
List other known quantities. |
1 L = 1000 mL |
| Plan the problem. | Rearrange the equation to solve for \(P_2\). \(P_2 = \dfrac{P_1 \times V_1}{V_2}\) |
| Calculate and cancel units. | \(0.663\;\cancel{\mathrm L}\times\dfrac{1000\;\mathrm{mL}}{1\;\cancel{\mathrm L}}=663\;\mathrm{mL}\) Substitute the known quantities into the equation and solve. \(P_2=\dfrac{722\;\mathrm{mm}\;\mathrm{Hg}\;\times\;88.8\;\cancel{\mathrm{mL}}}{663\;\cancel{\mathrm{mL}}}=96.7\;\mathrm{mm}\;\mathrm{Hg}\) |
Think about your result. |
The volume increased, so the pressure should have decreased, which it did (from 722 mm Hg to 96.7 mm Hg). |
✏️ Exercise \(\PageIndex{1}\)
- What pressure is required to compress a 124 mL of oxygen gas at 102 torr to a volume of 37.8 mL?
- Suppose that the pressure of 456 mL of helium at 5.96 psi was changed to 1.55 atm. What is the new volume of the helium, in units of milliliters?
- Answer A
- 335 torr (Note: temperature may be assumed to be constant in instances where temperature data is not provided.)
- Answer B
- 119 mL (Note: temperature may be assumed to be constant in instances where temperature data is not provided.)
Summary
- The behavior of gases can be modeled with gas laws.
- Boyle’s Law relates the pressure and volume of a gas at constant temperature and amount.
