9.3: Gas Pressure
- Page ID
- 289434
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)⚙️ Learning Objectives
- Define pressure.
- Learn the units of pressure and how to convert between them.
The kinetic molecular theory of gases indicates that gas particles are always in motion and are colliding with other particles and the walls of the container holding them. Although collisions with container walls are elastic (i.e., there is no net energy gain or loss because of the collision), a gas particle does exert a force on the wall during the collision. The accumulation of all these forces distributed over the area of the walls of the container causes something we call pressure. Pressure (P) is defined as the force of all the gas particle/wall collisions divided by the area of the wall:
\[\mathrm{pressure}=\dfrac{\mathrm{force}}{\mathrm{area}}\Rightarrow P=\dfrac FA\]
All gases exert pressure; it is one of the fundamental measurable quantities of this phase of matter. Even our atmosphere exerts pressure. In this case, the gas is being “held in” by the earth’s gravity, rather than the gas being in a container. The pressure of the atmosphere at sea level is about 14.7 pounds of force for every square inch of surface area: 14.7 lb/in2.
Pressure has a variety of units. The formal, SI unit of pressure is the pascal (Pa), which is defined as 1 N/m2 (one newton of force over an area of one square meter). However, this is usually too small in magnitude to be useful. A common unit of pressure is the atmosphere (atm), which was originally defined as the average atmospheric pressure at sea level.
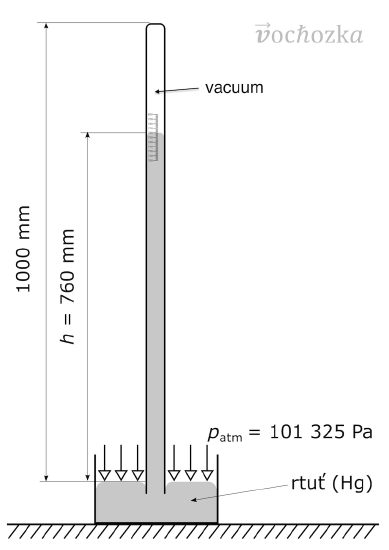
However, “average atmospheric pressure at sea level” is difficult to pinpoint because of atmospheric pressure variations. A more reliable and common unit is millimeters of mercury (mm Hg), which is the amount of pressure exerted by a column of mercury exactly 1 mm high. An equivalent unit is the torr, which equals 1 mmHg. The torr is named after Evangelista Torricelli, a seventeenth-century Italian scientist who invented the mercury barometer (see Figure \(\PageIndex{1}\)).
With these definitions of pressure, the atmosphere unit is redefined: 1 atm is defined as exactly 760 mm Hg, or 760 torr. We thus have the following equivalents:
1 atm = 760 mm Hg = 760 torr
Additional pressure conversions include:
1 atm = 29.92 in. Hg = 14.7 psi (14.7 lb/in2) = 101,325 Pa = 1.01325 bars
We can use these equivalents as with any equivalence – to perform conversions from one unit to another. A more complete set of conversions used throughout this text may be found in Section 17.2.
✅ Example \(\PageIndex{1}\): Pressure Conversion
Express a pressure of 11.7 psi in units of mm Hg and Pa.
Solution
| Steps for Problem Solving | |
|---|---|
| Identify the "given” information and what the problem is asking you to "find." | Given: 11.7 psi Find: ? mm Hg, ? Pa |
| List other known quantities. | 1 atm = 760 mm Hg 1 atm = 14.7 psi = 101,325 Pa Therefore, 760 mm Hg = 14.7 psi = 101,325 Pa |
| Prepare concept maps using the proper conversion factor(s). | \({\color[rgb]{0.8, 0.0, 0.0}\boxed{\;\;\;\;\mathrm{psi}\;\;\;\;}}\xrightarrow[{14.7\;\mathrm{psi}}]{760\;\mathrm{mm}\;\mathrm{Hg}}{\color[rgb]{0.0, 0.0, 1.0}\boxed{\;\mathrm{mm}\;\mathrm{Hg}\;}}\) \({\color[rgb]{0.8, 0.0, 0.0}\boxed{\;\;\;\mathrm{psi}\;\;\;}}\xrightarrow[{14.7\;\mathrm{psi}}]{101,325\;\mathrm{Pa}}{\color[rgb]{0.0, 0.0, 1.0}\boxed{\;\;\;\mathrm{Pa}\;\;\;}}\) |
| Calculate and cancel units. | \(11.7\;\cancel{\mathrm{psi}}\times\dfrac{760\;\mathrm{mm}\;\mathrm{Hg}}{14.7\;\cancel{\mathrm{psi}}}=605\;\mathrm{mm}\;\mathrm{Hg}\) \(11.7\;\cancel{\mathrm{psi}}\times\dfrac{101,325\;\mathrm{Pa}}{14.7\;\cancel{\mathrm{psi}}}=8.06\times10^4\;\mathrm{Pa}\) |
Think about your results. |
11.7 psi torr is less than 1 atm, as are the final answers. (605 mm Hg, 8.06×104 Pa) |
✏️ Exercise \(\PageIndex{1}\)
- How many atmospheres are there in 1,022 torr?
- Atmospheric pressure is low in the eye of a hurricane. In a 1979 hurricane in the Pacific Ocean, a pressure of 0.859 atm was reported inside the eye. What is this pressure in torr?
- Answer A
- 1.345 atm
- Answer B
- 653 torr
Summary
- Pressure is a force exerted over an area.
- Pressure has several common units that can be converted.
This page is shared under a CC BY-NC-SA 4.0 license and was authored, remixed, and/or curated by Marisa Alviar-Agnew, Lance S. Lund (Anoka-Ramsey Community College), and Henry Agnew.