9.5: Volume and Temperature
- Page ID
- 289439
⚙️ Learning Objectives
- Learn and apply Charles's Law.
Everybody enjoys the smell and taste of freshly-baked bread. It is light and fluffy as a result of the action of yeast on sugar. The yeast converts the sugar to carbon dioxide, which causes the dough to expand. The end result is an enjoyable treat, especially when covered with melted butter.
Charles's Law
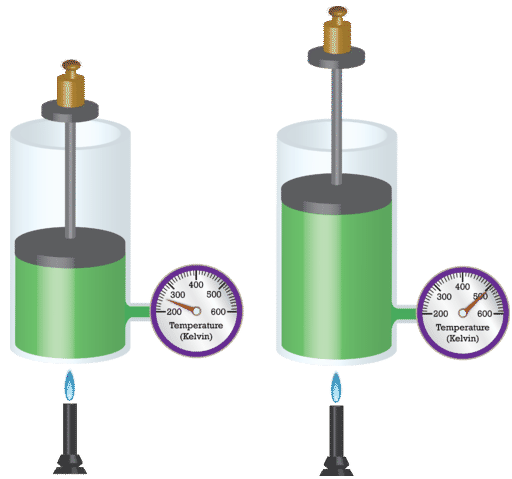
Consider the relationship between the volume of a gas (V) and its temperature (T), as shown in Figure \(\PageIndex{2}\). Change the temperature on the simulator on the right side of the figure by dragging the liquid level in the thermometer up and down. Notice the effect of changing the temperature on the volume.
(a)
French physicist Jacques Charles (1746-1823) studied the effect of temperature on the volume of a gas at constant pressure. Charles found that the volume of a given amount of gas increased in proportion with the absolute temperature of the gas. This means volume and absolute temperature are directly proportional, i.e. as one increases, the other increases in a proportionate manner. Or, as one decreases, the other decreases in a proportionate manner.
When two variables are directly proportional, doubling one variable causes the other to double as well. Reducing one variable to ⅕ of its original value will cause the other variable to decrease to ⅕ of its original. As a result, the ratio of the two variables remains constant. In the case of volume and absolute temperature,
\[\dfrac VT=\mathrm{constant}\]
Once again, this is for a given amount of gas at a constant pressure. If either volume or temperature changes while amount and pressure stay the same, then the other property must change so that the ratio of the two properties still equals that same constant. That is, if the original conditions are labeled \(V_1\) and \(T_1\) and the new conditions are labeled \(V_2\) and \(T_2\), we obtain
\[\dfrac{V_1}{T_1}=\dfrac{V_2}{T_2}\]
This relationship is known as Charles's Law. It is important to note that the temperatures are absolute temperatures. The absolute temperature is temperature measured with the Kelvin scale. The Kelvin scale must be used because zero on the Kelvin scale corresponds to a complete stop of molecular motion.
When volume and absolute temperature data are graphed, the result is a straight line, indicative of a direct proportion, shown in the figure below.
Notice that the line goes exactly toward the origin, meaning that as the absolute temperature of the gas approaches zero, its volume approaches zero. However, when a gas is brought to extremely cold temperatures, its molecules would eventually condense into the liquid state before reaching absolute zero. The temperature at which this change into the liquid state occurs varies for different gases.
The direct relationship will only hold if the temperatures are expressed in kelvins; Celsius temperatures will not work. Recall that TK = T°C + 273.15.
✅ Example \(\PageIndex{1}\):
A balloon is filled to a volume of 2.20 L at a temperature of 22°C. The balloon is then heated to a temperature of 71°C. Find the new volume of the balloon.
Solution
| Steps for Problem Solving | |
|---|---|
Identify the "given" information and what the problem is asking you to "find." |
Given: V1 = 2.20 L, T1 = 22°C = 295 K, T2 = 71°C = 344 K Find: V2 = ? L |
List other known quantities. |
The temperatures were first converted to kelvins. TK = T°C + 273.15 |
| Plan the problem. | Rearrange the equation to solve for V2. \(V_2 = \dfrac{V_1 \times T_2}{T_1}\) |
| Calculate and cancel units. | Substitute the given quantities into the equation and solve. \(V_2=\dfrac{2.20\;\mathrm L\;\times\;344\;\cancel{\mathrm K}}{295\;\cancel{\mathrm K}}=2.57\;\mathrm L\) |
| Think about your result. | The volume increases as the temperature increases. Note: Pressure was assumed to be constant. |
An air sample has a volume of 34.8 L and at −67ºC. What must be the temperature of the air, in ºC, for the volume to decrease to 25.0 L?
Solution
| Steps for Problem Solving | |
|---|---|
| Identify the "given" information and what the problem is asking you to "find." | Given: V1 = 34.8 L, T1 = –67ºC = 206 K, V2 = 25.0 L Find: T2 = ? K |
| List other known quantities. | The temperatures were first converted to kelvins. TK = T°C + 273.15 |
| Plan the problem. | Rearrange the equation to solve for T2. \(\dfrac{V_1}{T_1}=\dfrac{V_2}{T_2}\) Cross multiply to yield \(V_1\times T_2=V_2\times T_1\) \(\dfrac{\displaystyle\cancel{V_1\times}T_2}{\cancel{V_1}}=\dfrac{\displaystyle V_2\times T_1}{V_1}\Rightarrow\boxed{T_2=\dfrac{\displaystyle V_2\times T_1}{V_1}}\) |
| Calculate and cancel units. | Substitute the known quantities into the equation and solve. \(T_2=\dfrac{\displaystyle V_2\times T_1}{V_1}=\dfrac{(25.0\;\cancel{\mathrm L})(206\;\mathrm K)}{34.8\;\cancel{\mathrm L}}=148\;\mathrm K\) T°C = TK – 273.15 = 148 – 273.15 = −125ºC |
| Think about your result. | The temperature decreased, meaning the volume decreased (which it did). Note: Pressure was assumed to be constant. |
✏️ Exercise \(\PageIndex{1}\)
- What is the volume of a balloon if it was initially filled with helium to a volume of 3.77 L at –18°C and cooled much further to a temperature of –150°C?
- A sample of nitrogen gas has a volume of 277 mL at −38°C. If the sample originally had a volume of 623 mL, what was its temperature at that volume, in °C?
- Answer A
- 1.82 L
- Answer B
- 256°C
Summary
- Charles’s Law relates the volume and temperature of a gas at constant pressure and amount.
