8.7: Ionization of Water and The pH Scale
- Page ID
- 432734
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)↵
- Define and use the ion product constant for water to calculate concentrations of H3O+ and OH− in aqueous solutions.
- Define the pH scale and use it to describe acids and bases.
Ionization of Water
As we have already seen, H2O can act as an acid or a base. Within any given sample of water, some H2O molecules are acting as acids, and other H2O molecules are acting as bases. The chemical equation is as follows:

Similar to a weak acid, the autoionization of water is an equilibrium process, and is more properly written as follows:
H2O(ℓ)+H2O(ℓ) ⇌ H3O+(aq)+OH−(aq)
The equilibrium constant for the autoionization of water is referred to as the ion-product for water and is given the symbol Kw.
Kw = [H3O+][OH−]
The ion-product constant for water (Kw) is the mathematical product of the concentration of hydronium ions and hydroxide ions. Note that H2O is not included in the ion-product expression because it is a pure liquid. The value of Kw is very small, in accordance with a reaction that favors the reactants. At 25oC, the experimentally determined value of Kw in pure water is 1.0×10−14.
Kw = [H3O+][OH−] = 1.0×10−14
In a sample of pure water, the concentrations of hydronium and hydroxide ions are equal to one another. Pure water or any other aqueous solution in which this ratio holds is said to be neutral.
[H3O+] = [OH−] = 1.0×10−7
The product of these two concentrations is 1.0×10−14
[H3O+]×[OH−]=(1.0×10−7)(1.0×10−7)=1.0×10−14
- For acids, the concentration of H3O+ is greater than 1.0×10−7 M
- For bases, the concentration of OH− is greater than 1.0×10−7 M.
No matter whether the aqueous solution is an acid, a base, or neutral the Kw remains constant.
- For acidic solutions, [H3O+] is greater than [OH−].
- For basic solutions, [OH−] is greater than [H3O+].
- For neutral solutions, [H3O+] = [OH−] = 1.0×10−7M
NOTE: It is rare to truly have pure water. Water exposed to air will usually be slightly acidic because dissolved carbon dioxide gas, or carbonic acid, decreases the pH slightly below 7. Alternatively, dissolved minerals, like calcium carbonate (limestone), can make water slightly basic.
Knowing the amount of acid and base in solutions is extremely important for a wide variety of applications ranging from brewing beer or wine to studying the effects of river and creek water acidification to health and medicine. Scientists are good at calculating and measuring the concentration of hydronium in a solution, however, there is a more convenient way to make comparisons between solutions – the pH scale.
The pH Scale
One qualitative measure of the strength of an acid or a base solution is the pH scale, which is based on the concentration of the hydronium in aqueous solution.
\[pH = -\log[H_3O^+] \nonumber \]
Figure \(\PageIndex{1}\) illustrates this relationship, along with some examples of various solutions. Because hydronium ion concentrations are generally less than one (for example \(1.3 \times 10^{-3}\,M\), the log of the number will be a negative number. To make pH even easier to work with, pH is defined as the negative log of \([H_3O^+]\), which will give a positive value for pH. Note that [H3O+] may be addressed as [H+].
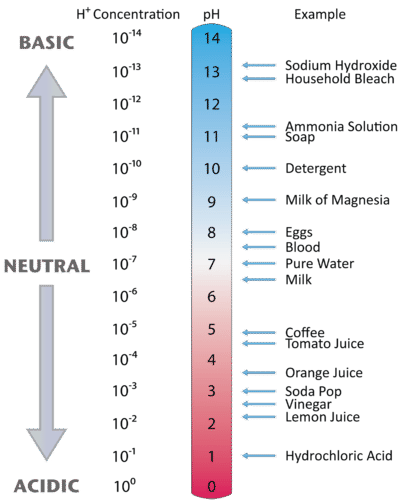
A neutral (neither acidic nor basic) solution has a pH of 7. A pH below 7 means that a solution is acidic, with lower values of pH corresponding to increasingly acidic solutions. A pH greater than 7 indicates a basic solution, with higher values of pH corresponding to increasingly basic solutions. Thus, given the pH of several solutions, you can state which ones are acidic, which ones are basic, and which are more acidic or basic than others. These are summarized in table below.
Table \(\PageIndex{1}\): Acidic, Basic and Neutral pH Values
| Classification | Relative Ion Concentrations | pH at 25 °C |
|---|---|---|
| acidic | [H3O+] > [OH−] | pH < 7 |
| neutral | [H3O+] = [OH−] | pH = 7 |
| basic | [H3O+] < [OH−] | pH > 7 |
Find the pH, given the [H3O+] of the following:
- 1 ×10-3 M
- 2.5 ×10-11 M
- 4.7 ×10-9 M
Solution
pH = - log [H3O+]
Substitute the known quantity into the equation and solve. Use a scientific calculator for b and c.
- pH = - log [1 × 10−3 ] = 3.0 (1 decimal place since 1 has 1 significant figure)
- pH = - log [2.5 ×10-11] = 10.60 (2 decimal places since 2.5 has 2 significant figures)
- pH = - log [4.7 ×10-9] = 8.33 (2 decimal places since 4.7 has 2 significant figures)
Note on significant figures:
Because the number(s) before the decimal point in the pH value relate to the power on 10, the number of digits after the decimal point (underlined) is what determines the number of significant figures in the final answer.
Exercise \(\PageIndex{1}\)
Find the pH, given [H3O+] of the following:
- 5.8 ×10-4 M
- 1.0×10-7 M
- Answer
-
a. 3.24
b. 7.00
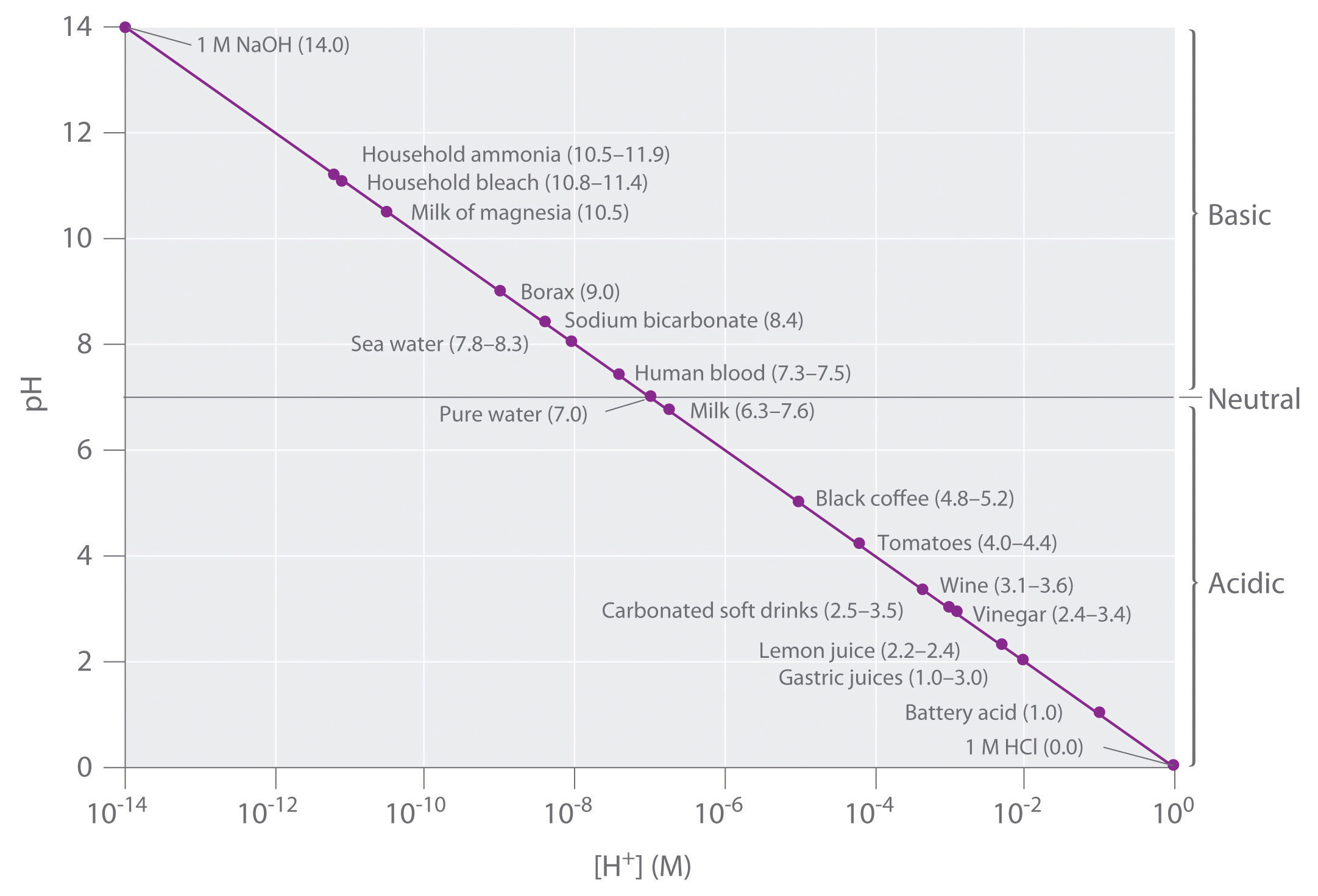
Figure \(\PageIndex{2}\) lists the pH of several common solutions. The most acidic among the listed solutions is 1 M HCl with the lowest pH value (0.0): battery acid is the next most acidic solution with a pH value of 0.3. The most basic is 1M NaOH solution with the highest pH value of 14.0. Notice that some biological fluids (gastric juices and blood) are not neutral. You may also notice that many food products are slightly acidic. They are acidic because they contain solutions of weak acids. If the acid components of these foods were strong acids, the food would likely be inedible.
Label each solution as acidic, basic, or neutral based only on the stated \(pH\).
- milk of magnesia, pH = 10.5
- pure water, pH = 7
- wine, pH = 3.0
Solution
- With a pH greater than 7, milk of magnesia is basic. (Milk of magnesia is largely Mg(OH)2.)
- Pure water, with a pH of 7, is neutral.
- With a pH of less than 7, wine is acidic.
Exercise \(\PageIndex{2}\)
Identify each substance as acidic, basic, or neutral based only on the stated \(pH\).
- human blood with \(pH\) = 7.4
- household ammonia with \(pH\) = 11.0
- cherries with \(pH\) = 3.6
- Answer
-
a. slightly basic
b. basic
c. acidic
Measuring pH
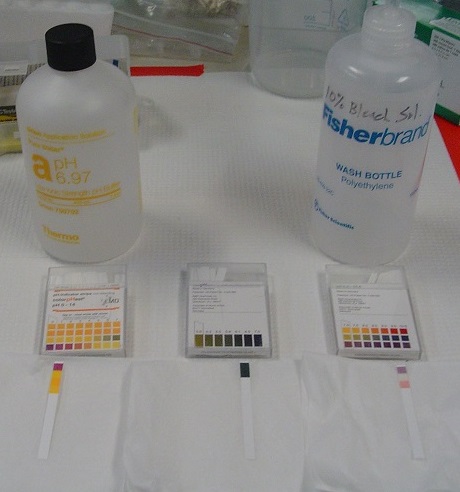
Tools have been developed that make the measurement of pH simple and convenient (Figures 8.7.3). For example, pH paper consists of strips of paper impregnated with one or more acid–base indicators, which are intensely colored organic molecules whose colors change dramatically depending on the pH of the solution. Placing a drop of a solution on a strip of pH paper and comparing its color with standards give the solution’s approximate pH. A more accurate tool, the pH meter, uses a glass electrode, a device whose voltage depends on the H+ ion concentration (Figure \(\PageIndex{3}\)).

Normal rainwater has a pH between 5 and 6 due to the presence of dissolved CO2 which forms carbonic acid:
\[\ce{H2O (l) + CO2(g) ⇌ H2CO3(aq)} \label{14} \]
H2CO3 (aq) + H2O (l) ⇌ H3O+(aq) + HCO3- (aq)
Acid rain is rainwater that has a pH of less than 5, due to a variety of nonmetal oxides, including CO2, SO2, SO3, NO, and NO2 being dissolved in the water and reacting with it to form not only carbonic acid, but sulfuric acid and nitric acid. The formation and subsequent ionization of sulfuric acid are shown here:
\[\ce{H2O (l) + SO3(g) ⇌ H2SO4(aq)} \label{16} \]
H2SO4(aq) + H2O (l) → H3O+(aq)+ HSO4- (aq)
Carbon dioxide is naturally present in the atmosphere because we and most other organisms produce it as a waste product of metabolism. Carbon dioxide is also formed when fires release carbon stored in vegetation or when we burn wood or fossil fuels. Sulfur trioxide in the atmosphere is naturally produced by volcanic activity, but it also stems from burning fossil fuels, which have traces of sulfur, and from the process of “roasting” ores of metal sulfides in metal-refining processes. Oxides of nitrogen are formed in internal combustion engines where the high temperatures make it possible for the nitrogen and oxygen in air to chemically combine.
Acid rain is a particular problem in industrial areas where the products of combustion and smelting are released into the air without being stripped of sulfur and nitrogen oxides. In North America and Europe until the 1980s, it was responsible for the destruction of forests and freshwater lakes, when the acidity of the rain actually killed trees, damaged soil, and made lakes uninhabitable for all but the most acid-tolerant species. Acid rain also corrodes statuary and building facades that are made of marble and limestone (Figure \(\PageIndex{4}\)). Regulations limiting the amount of sulfur and nitrogen oxides that can be released into the atmosphere by industry and automobiles have reduced the severity of acid damage to both natural and manmade environments in North America and Europe. It is now a growing problem in industrial areas of China and India.

Figure \(\PageIndex{4}\): (a) Acid rain makes trees more susceptible to drought and insect infestation, and depletes nutrients in the soil. (b) It also is corrodes statues that are carved from marble or limestone. (credit a: modification of work by Chris M Morris; credit b: modification of work by “Eden, Janine and Jim”/Flickr)


