4.2: Legendre Transforms
- Page ID
- 5166
The microcanonical ensemble involved the thermodynamic variables \(N\), \(V\) and \(E\) as its variables. However, it is often convenient and desirable to work with other thermodynamic variables as the control variables. Legendre transforms provide a means by which one can determine how the energy functions for different sets of thermodynamic variables are related. The general theory is given below for functions of a single variable.
Consider a function \(f(x)\) and its derivative
\[y=f'(x) = {df \over dx} \equiv g(x) \nonumber \]
The equation \(y = g (x) \) defines a variable transformation from \(x\) to \(y\). Is there a unique description of the function \(f(x)\) in terms of the variable \(y\)? That is, does there exist a function \(\phi (y) \) that is equivalent to \(f(x)\)?
Given a point \(x_0\), can one determine the value of the function \(f (x_0)\) given only \(f' (x_0)\) ? No, for the reason that the function \( f (x_0) + c \) for any constant \(c\) will have the same value of \( f' (x_0 ) \) as shown in Figure \(\PageIndex{1}\).
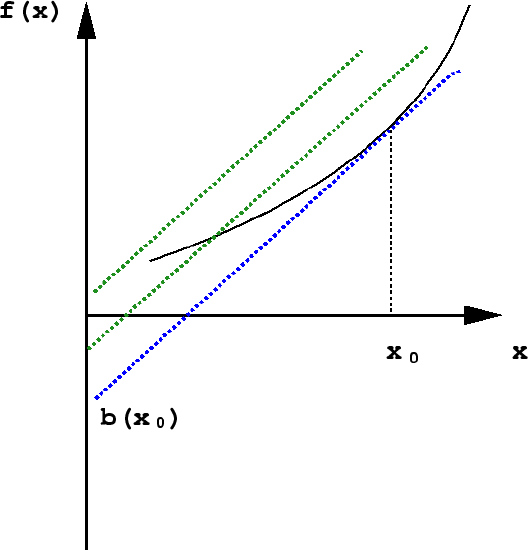
However, the value \(f (x_0)\) can be determined uniquely if we specify the slope of the line tangent to \(f\) at \(x_0\), i.e., \(f' (x_0) \) and the \(y\)-intercept, \(b (x_0)\) of this line. Then, using the equation for the line, we have
\[ f (x_0) = x_0 f' (x_0 ) + b ( x_0 ) \nonumber \]
This relation must hold for any general \(x\):
\[ f (x) = x f' (x) + b (x) \nonumber \]
Note that \(f' (x)\) is the variable \(y\), and \( x = g^{-1} (y) \), where \(g_{-1} \) is the functional inverse of \(g\), i.e., \(g ( g^{-1} (x) ) = x \). Solving for \( b (x) = b ( g^{-1} (y) ) \) gives
\[ b (g^{-1} (y)) = f ( g^{-1} (y)) - y g^{-1} (y) \equiv \phi (y) \nonumber \]
where \(\phi (y) \) is known as the Legendre transform of \(f (x) \). In shorthand notation, one writes
\[ \phi (y) = f (x) - xy \nonumber \]
however, it must be kept in mind that \(x\) is a function of \(y\).


