Significant Figures
- Page ID
- 354
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Significant figures are used to keep track of the quality (variability) of measurements. This includes propagating that information during calculations using the measurements. The purpose of this page is to help you organize the information about significant figures -- to help you set priorities. Sometimes students are overwhelmed by too many rules, and lack guidance about how to sort through them. What is the purpose? Which rules are most important?
The following points as being most important:
- Significant Digits relate to measurements. When you think about how many Significant Digits a number has, think about where the number came from.
- The most important rule for handling Significant Digits when doing calculations is the rule for multiplication.
I will de-emphasize the following:
- Whether zeroes are significant.
- The rules for handling Significant Digits in other types of calculations.
What if the advice given here disagrees with what your book or instructor says?
Let's break that into two parts. One is about the information per se, and the other is about priorities, about the approach to thinking about Significant Digits. The information here should agree, for the most part. However, what may be different is the order of presenting things, with a different perspective in the approach -- the steps -- to learning Significant Digits. We will all end up in the same place.
If you were completely happy with how the Significant Digits topic is presented in your own course, you probably wouldn't be reading this page. Think of it as another approach -- to the same thing. Sometimes, looking at things differently can help. Trying two approaches can be better than trying only one. There is no claim that one approach is "right" or even "better". If there is a discrepancy between any information here and your own course, please let me know -- or check with your own instructor. Some details are a matter of preference. In the lab. When you take a measurement, you record not only the value of the measurement, but also some information about its quality. Using Significant Digits is one simple way to record the quality of the information.
A simple and useful statement is that the significant figures (Significant Digits) are the digits that are certain in the measurement plus one uncertain digit.
Significant Digits is not a set of arbitrary rules. Almost everything about Significant Digits follows from how you make the measurements, and then from understanding how numbers work when you do calculations. Unfortunately, there are "special cases" that can come up with Significant Digits. If all the rules are presented together, it is easy to get lost in the rules. Better -- and what we will do here -- is to emphasize the logic of using Significant Digits. This involves a few basic ideas, which can be stated as rules. We will leave special cases for a while, so they do not confuse the big picture. The number of high priority rules about Significant Digits is small.
The best way to start with Significant Digits is in the lab, taking measurements. An alternative is to use an activity that simulates taking measurements -- of various accuracy. We will do that here, using drawings of measurement scales. A bad way to start with Significant Digits is to learn a list of rules.
How many significant figures does a measurement have?
When you take a measurement, you write down the correct number of digits. You write down the significant digits. That is, the way you write a number conveys some information about how accurate it is. It is up to you to determine how many digits are worth writing down. It is important that you do so, since what you write conveys not only the measurement but something about its quality. For many common lab instruments, the proper procedure is to estimate one digit beyond those shown directly by the measurement scale. If that one estimated digit seems meaningful, then it is indeed a significant digit.
The scale shown here is a "typical" measurement scale. The specific scale is from a 10 mL graduated cylinder -- shown horizontally here for convenience. The arrow marks the position of a measurement.
Glossary entry: Scale.
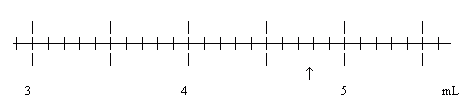
Our goal is to read the scale at the position of the arrow. Let's go through this in detail.
- The numbered lines are 1 mL apart.
- The little lines (between the numbered lines) are 0.1 mL apart.
- The arrow is clearly between 4.7 and 4.8 mL.
- We will estimate the position of the arrow to 1/10 the distance between the little lines, that is, to the nearest 0.01 mL. (It is a common rule of thumb to estimate the last digit to 1/10 the distance between the lines. This corresponds, of course, to writing one more digit "as best we can".)
- A reasonable estimate is 4.78 mL. Some people might say 4.77 mL or 4.79 mL. No one should say 4.72 mL! That is, the estimate is 4.78 mL to about +/- 0.01 mL. 4.78 mL is 3 Significant Digits; the last Significant Digits is not certain, but is "close".
How meaningful is a drawing of a measurement scale, such as the one in the example above? It illustrates one particular issue very well: how to read a scale per se, figure out what the marks and labels mean, and how to estimate the final digit. Real measuring instruments, such as graduated cylinders, have those issues. Depending on the situation, there may be other issues that affect the ease of reading. In the drawing above, the goal is to read a well-defined arrow. With a real graduated cylinder, you may need to deal with a meniscus (curved surface) and parallax. Those issues are beyond our topic here.
A final zero? In estimating that last digit, be sure to write down the zero if your best estimate is indeed zero. For example, if the last digit reflects hundredths of a mL, you might estimate in one case that there are 6 hundredths; thus you would write 6 as the last digit (e.g., 8.16 mL -- 3 Significant Digits). But you might (in another case) estimate that there are 0 hundredths; it is important that you write that zero (e.g., 8.10 mL -- 3 Significant Digits). That final zero says you looked for hundredths and found none. If you wrote only 8.1 mL (2 Significant Digits), it would imply that you did not look for hundredths.
The arrow below appears to be "right on" the "4.7" line. (Let's assume that. The point here is to deal with the case where you think the arrow is "on" the line.) Thus we estimate that the hundredths place is 0. The proper reading, then, is 4.70 mL (3 Significant Digits). That final zero means that we looked for hundredths, and found none. If we wrote 4.7 mL (2 Significant Digits), it would imply that we didn't look for hundredths.
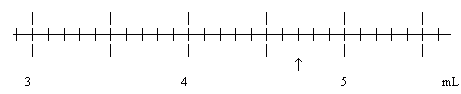
The scale shown in Example 2 is the same scale as in Example 1. In Example 1 our proper reading had 3 Significant Digits. That is also true in Example 2. That final 0 in Example 2 is an estimate; it is entirely equivalent to the final 8 estimated in Example 1.
When I look at a measurement that someone else has given me, how can I tell how many significant figures it has?
There are a couple of ways to approach this:
- You can look at the number and analyze the digits, using your rules for Significant Digits.
- You can think about the measurement scale that resulted in this measurement. Think about how the scale was read, with one digit being estimated.
Both approaches will work. They reflect the same principles. Often, simply looking at the number will be sufficient. However, when you are not sure, it helps to go back to basics: think about the underlying measurement. We will illustrate this in the next section, on zeroes -- the situation most likely to cause confusion.
What about the zeroes? Are they significant or not?
We tend to spend more time on this issue than it really is worth. Only one tenth of all digits are zeroes, yet the bulk of a list of Significant Digits rules may be about how to treat the zeroes. Many zeroes are clear enough, but indeed it can take a bit of thought to decide whether some zeroes are or are not significant.
If you understand where Significant Digits come from, then whether a zero is significant should be clear -- at least most of the time. If you are learning Significant Digits by memorizing rules, then you are doing it the hard way -- not understanding the meaning. If, for whatever reason, you are struggling with Significant Digits, the problem of the zeroes is a low priority problem.
Here is what I usually suggest to students. Don't worry too much about the rules for zeroes, especially when you are just starting. As you go on, ask about specific cases where you are not sure about the zeroes. That way, you will gradually learn how to deal with the zeroes, but not get bogged down with what can seem to be a bunch of picky rules.
The key point in deciding whether a zero is significant is to decide if it is part of the measurement, or simply a digit that is there to "fill space". The next section will help with much of the "zeroes problem".
Why is scientific notation helpful?
When a number is written in standard scientific (exponential) notation format, there should be no problem with zeroes. In this format, with one digit before the decimal point and only Significant Digits after the decimal point, all digits shown are significant.
How many Significant Digits are in the measurement 0.00023456 m?
Solution
In scientific notation that is 2.3456x10-4 m. 5 Significant Digits. Scientific notation makes clear that all the zeroes to the left are not significant. The first zero is just decorative and could be omitted; the others are place-holders, so you can show that the 2 is the fourth decimal place.
The "rule" that covers this case may be stated: zeroes on the left end of a number are not significant -- regardless of where the decimal point is. Hopefully, the example, showing how this plays out in scientific notation, makes this rule clearer.
How many Significant Digits are in the measurement 0.00023450 m?
Solution
In scientific notation that is 2.3450x10-4 m. 5 Significant Digits. That final zero is part of the measurement. If it weren't, why would it be there?
The "rule" that covers this case may be stated: zeroes on the right end of a number are significant -- if they are to the right of the decimal point. This rule may seem confusing in words, but showing the case in scientific notation should make it clearer.
How many Significant Digits are in the measurement 234000 m?
Solution
In scientific notation that is ... Hm, what is it? It's not really clear. Let's suggest that it is 2.34x105 m. That is clearly 3 Significant Digits.
Why did I choose to not consider the zeroes significant? Maybe they are significant. Or maybe one of them is significant. The problem is that there is no way to tell from the number 234000 whether those zeroes are significant or are merely place holders, telling us (for example) that the 4 is in the thousands place. So why choose to make them not significant? First, that is the conservative position. I don't know whether they are significant, and to claim that they are is an unwarranted claim of quality. Second, 3 Significant Digits is reasonable -- a common way to measure distances; 6 Significant Digits is not likely. What if the person making the measurement knows that the measurement is good to 4 Significant Digits, with the first zero being significant? Then, somehow, they need to say so. One good way is to put the measurement in proper scientific notation in the first place: 2.340x105 m, 4 Significant Digits.
How do I handle significant figures in calculations?
It depends on the type of calculation. Each math operation has its own rules for handling Significant Digits. More precisely, there is one rule each for:
- multiplication and division (which are basically the same thing, so they share a rule);
- addition and subtraction (which are basically the same thing, so they share a rule);
- logs and antilogs (which are basically the same thing, so they share a rule).
Those three rules are distinct; you must be careful to use the right rule for the right operation. But there is good news: The multiplication rule is by far the most important in basic chemistry -- and it is perhaps also the simplest. So, as a matter of priority, emphasize the multiplication rule. When you have mastered it, you can go on and learn the addition rule. It is useful, though much less important. Whether you need the rule for logs will depend on your course; some courses manage to avoid this rule completely.
In summary ... there are three rules, but there is a clear set of priorities with them. Emphasize the multiplication rule. It is the most important rule, and the easiest one.
Multiplication Rule
If you multiply two numbers with the same number of Significant Digits, then the answer should have that same number of Significant Digits. If you multiply together two numbers that each have 4 Significant Digits, then the answer should have 4 Significant Digits.
Multiply 12.3 cm by 2.34 cm.
Solution
Doing the arithmetic on the calculator gives 28.782. In this case, each number has 3 Significant Digits. Thus we report the result to 3 Significant Digits. Proper rounding of 28.782 to 3 Significant Digits gives 28.8. With the units, the final answer is 28.8 cm2.
If you multiply together two numbers with different numbers of Significant Digits, then the answer should have the same number of Significant Digits as the "weaker" number. Hm, that is a lot of words. An example should help. Multiply a number with 3 Significant Digits and a number with 4 Significant Digits. Keep 3 Significant Digits in the answer.
Multiply 24 cm by 268 cm.
Solution
Doing the arithmetic on the calculator gives 6432. One measurement has 2 Significant Digits and one has 3 Significant Digits. The 2 Significant Digits number is "weaker": it has less information; it has only two digits of information in it. That is, the 2 Significant Digits number limits the calculation. Thus we report the result to 2 Significant Digits. Proper rounding of 6432 to 2 Significant Digits gives 6400. That is clearer in scientific notation, as 6.4x103. With the units, the final answer is 6.4x103 cm2. [Recall section Why is scientific notation helpful?, especially Example 5.]
The following two examples serve as reminders that it is important to understand the context of the particular problem. In Example 7, we reported the product of 24 & 268 to 2 Significant Digits. But in Example 8, which follows, we report the product of those same two numbers to 3 Significant Digits. Both are correct -- because the contexts are different. Example 9 reminds us of another issue in carefully recording measurements.
You have an object that is 268 cm long. What would be the total length of 24 such objects?
Solution
The calculator gives 6432, as in Example 7. Now we look at the Significant Digits; we must carefully think about what each number means. "268 cm" is an ordinary measurement; it has 3 Significant Digits. But the "24" is a count, and is taken as exact (with no uncertainty). That is, the "24" does not limit the calculation, and we report 3 Significant Digits. With the units, the final answer is 6.43x103 cm.
You measure the sides of a rectangle. The sides are 28.2 cm and 25 cm. What is the area? But before you calculate the area... There is probably something wrong with the statement of this question. What?
What's wrong? Well, we have an object, approximately square. Someone has measured two sides. One would think they used the same measuring instrument -- the same ruler. But the two reported measurements are inconsistent. One is reported to the nearest cm, and one is reported to the nearest tenth. That is suspicious. Why were they not reported the same way?
The purpose of this example is to remind you of the importance of reading the measuring instrument carefully and consistently, and recording the final zero if indeed that is your estimate. There is no need to carry out the calculation in this case.
Notes...
- The position of the decimal point is irrelevant in determining Significant Digits for multiplication. Just count how many Significant Digits there are.
- We discussed the multiplication rule for the case of multiplying two numbers. If there are more than two numbers, the rule is the same. You can think of this as multiplying two numbers at a time.
- Multiplication and division are basically the same operation. Dividing by "x" is equivalent to multiplying by "1/x". The rule for Significant Digits is the same for multiplication and division, and for operations involving any combination of them.
- Ordinary calculators have no idea about Significant Digits at all. They may give you too many digits or too few digits. Use the calculator to do the arithmetic, but then you take responsibility for the Significant Digits.
Addition Rule
For students who are just starting chemistry, the addition rule for Significant Digits is not as important as the multiplication rule. The intent of that statement is to help you set priorities. Learn one thing at a time -- especially if you are finding the topic difficult. The multiplication rule is more important; learn it first and get comfortable with it.
Most instructors will want you to learn the addition rule. I am not suggesting otherwise. Again, the emphasis here is to guide you to learn one thing at a time.
Here is an example of a basic chem situation that would seem to involve the addition rule, yet where using that rule is not really needed. Consider calculating the molar mass (formula weight) of a compound, say KOH. Using the atomic masses shown on the periodic table, the molar mass of KOH is 39.10 + 16.00 + 1.008 = 56.108 (in g/mol).
So, how many Significant Digits do we keep?
One answer might be to use the Significant Digits rule for addition and note that the result is only good to the hundredths place. Therefore, we round it to 56.11 g/mol.
However, that may be unnecessary -- and even undesirable. The reason for calculating a molar mass is to use it in a real calculation. In real cases, it is usually fine to calculate molar mass by using the atomic masses shown on your periodic table. No rounding, at least now. When you use the molar mass for a calculation, you round the final result. At this step, you should -- in principle -- consider the quality of the molar mass number. However, in practice, it is likely to not matter. It is most likely -- especially in beginning chemistry -- that the Significant Digits of the final result will be limited by other parts of the calculation, not the molar mass.
Therefore, I encourage beginning students to use the procedure above... Use all the digits of the atomic weights shown on their periodic table. Just add them up, and use the molar mass you get. Don't round the molar mass. Round the final result for the overall calculation, assuming that the molar mass Significant Digits is not a concern. This is usually fine, and lets you worry about the addition rule a bit later.
Now, it is easy enough for the textbook to make up problems where the above method would not be satisfactory. My point is that such cases are uncommon in real problems, especially in introductory chemistry. In fact, a simple example of a question is "Calculate the molar mass of ... [some chemical]." How many Significant Digits do you report? Well, you'll need to use the addition rule for Significant Digits. But that is an artificial question; in the real world one almost always wants to know a molar mass in the context of a specific calculation involving some measurement, and it is quite likely that the measurement will limit the quality of the result.
Logarithm Rule
The logarithm of 74 is 1.87. (We will use base 10 logs here, but the Significant Digits rule is the same in any case.) 74 has 2 Significant Digits, and the log shown, 1.87, has 2 Significant Digits. Why? Because the 1 in the log (the part before the decimal point -- the "characteristic") relates to the exponent, and is an "exact" number.
Whoa! What exponent? Well, it will help to put the number in standard scientific notation. 74 is 7.4x101. Now consider the log of each part: the log of 101 is 1, an exact number; the log of 7.4 is 0.87 -- with a proper 2 Significant Digits. Add those together, and you get log 74 = 1.87 -- with 2 Significant Digits.
Log of 740,000? That is log of 7.4x105. 5.87. In scientific notation only the exponent is different from the previous number; therefore in the logarithm, only the leading integer is different.
This log rule is often skipped in an intro chem course for a couple of reasons. First, logs may come up only once, with pH. Second, students in an intro chem course often are weak with using exponents -- and may not have learned about logs at all. So, sometimes one just suggests that pH be reported to two decimal places -- a usable if rough approximation.
Should I round off to the proper number of significant figures at each step?
The short answer is "no".
It is common now that most calculations are done on a calculator. Just do all the steps with the calculator, letting the machine keep track of the intermediate results. There is no need to even write down intermediates, much less round them. Why avoid rounding at each step? Each time you round, you are throwing away some information. If you do it over and over, it gets worse and worse; you accumulate rounding errors -- and that is not so good.
Imagine that we want to calculate 1.00 * (1.127)10. For our purposes here, the numbers are measurements, and we are to give the answer with proper Significant Digits. Proper Significant Digits in this case is 3 (because 1.00 is 3 Significant Digits). (For a clarification, see * note at end of this example box.)
We might consider two ways to do this:
- Do the indicated calculation; then, at the end, round to 3 Significant Digits. This gives 3.31.
- First round the 1.127 to 3 Significant Digits: 1.13. Now do the calculation and round the answer to 3 Significant Digits. This gives 3.39.
Well, those two calculations give answers that are quite different! How can we judge them? Here is one approach... The original number 1.127, by convention, means 1.127 +/- 0.001. That is, this measurement might be 1.126 to 1.128. If we do the calculation with 1.126, we get 3.28. If we do the calculation with 1.128, we get 3.34. Thus it seems that the result should be in the range of those two numbers, 3.28-3.34. In fact, method 1 (calculate with the original number and round only at the end) gives 3.31 -- which is in the middle of that range. However, method 2 (round first), gives 3.39 -- which is outside the range, by quite a bit. The reason should be clear enough in this example: we have rounded "up" ten times, and thus biased the result upwards. This is an example of how rounding errors can accumulate. It is better to round only at the end.
At the start of this example we said that the proper number of Significant Digits in this case was 3. As we went on, we found that the range of possible answers was 3.28-3.34, or 3.31 +/- 0.03. Obviously, this means that stating the answer as 3.31, to 3 Significant Digits with an implication of +/- 0.01, is not so good. This illustrates a limitation of Significant Digits; it is not so good when there are many error terms to keep track of (10, in this case). The main point of this example was to show the effect of compounding rounding errors -- hence the desirability of not rounding off at intermediate stages. (For more about such limitations of Significant Digits, see the section below: Limitations and complications of Significant Digits.)
The discussion of Significant Digits when adding up atomic weights to calculate a molecular weight, in the section Significant figures in addition, is consistent with this point. The question of how to round when the final digit is a 5 -- or at least appears to be a 5 -- is discussed below in the Special cases section on Rounding: What to do with a final 5.
Conversion factors
How many Significant Digits do conversion factors have? Well, it depends. Conversion factors within the metric system, i.e., involving only metric prefixes, are exact. Similarly, conversion factors between large and small units within the American system (e.g., 12 inches per foot, are exact). Conversion factors between metric and American systems are typically not exact, and it is your responsibility to try to make sure you use a conversion factor that has enough Significant Digits for your case. It is generally not good to allow a conversion factor to limit the quality of a calculation.
The conversion factor between centimeters and inches, 2.54 cm = 1 inch, is exact -- because it has been defined to be exact. If you convert 14.626 cm to inches, at 2.54 cm/inch, you can properly report the result as 5.7583 inches -- 5 Significant Digits, like the original measurement -- because the conversion factor is exact.
Many conversion factors we use in chemistry relate one property to another. Examples are density (mass per volume, g/mL) and molar mass (mass per mole, g/mol). These conversion factors are based on measurements, and their Significant Digits must be considered. It is your responsibility to think about the Significant Digits of a conversion factor. The best approach is usually to think about where the number came from. Is it a definition? a measurement?
Limitations and complications of Significant Digits
Using Significant Digits can be a good simple way to introduce students to the idea of measurement errors. It allows us to begin to relate the measurement scale to measurement quality, and does not require much math to implement. However, Significant Digits are only an approximation to true error analysis, and it is important to avoid getting bogged down in trying to make Significant Digits work well when they really don't.
One type of difficulty with Significant Digits can be seen with reading a scale to the nearest "tenth". (The scale shown with Example 1 illustrates this case.) In this case, 1.1 and 9.1 are both proper measurements. If we assume for simplicity that each measurement is good to +/- 0.1, the uncertainty in the first measurement is about 10% and the uncertainty in the second measurement is about 1%. Clearly, simply saying that both numbers are good to two Significant Digits is only a rough indication of the quality of the measurement.
Further, Significant Digits does not convey the magnitude of the reading uncertainty for any specific scale. The common statement, which I used in the previous paragraph, is that readings are assumed to be good to 1 in the last place shown. But on some scales, it would be much more realistic to suggest that the uncertainty is 2 or even 5 in the last place shown. A similar problem can occur when the errors from many numbers are accumulated in one calculation. Example 10 illustrated this.
Another limitation of Significant Digits is that it deals with only one source of error, that inherent in reading the scale. Real experimental errors have many contributions, including operator error and sometimes even hidden systematic errors. One cannot do better than what the scale reading allows, but the total uncertainty may well be more than what the Significant Digits of the measurements would suggest.
I have found that, even in introductory courses, some of the students will realize some of these limitations. When they point them out to me, I am happy to compliment them on their understanding. I then explain that Significant Digits is a simple and approximate way to start looking at measurement errors, and assure them that more sophisticated -- but more labor-intensive -- ways are available.
Scale Reading: Digital instruments
Some modern measuring instruments have a digital scale. Electronic balances are particularly common. How do you know how many Significant Digits to write down from a digital scale? Good question. Most such instruments will display the proper number of digits. However, you should watch the instrument and see if that seems reasonable. Remember that we usually estimate one digit beyond what is certain. With a digital scale, this is reflected in some fluctuation of the last digit. So if you see the last digit fluctuating by 1 or 2, that is fine. Write down that last digit; you should try to write down a value that is about in the middle of the range the scale shows.
If the fluctuation is more than 2 or so in the last digit, it may mean that the instrument is not working properly. For example, if the balance display is fluctuating much, it may mean that the balance is being influenced by air currents -- or by someone bumping the bench. Regardless of the reason, a large fluctuation may mean that a displayed digit is not really significant.
Scale Reading: Volumetric pipets or volumetric flasks
These measuring instruments have only one calibration line. You adjust the liquid level to the calibration line -- as close as you can; you then have the volume that is shown on the device. A 10 mL volumetric pipet measures 10 mL; that is the only thing it can do. So, how many Significant Digits do we report in such a measurement? Obviously the usual procedures for determining Significant Digits are not applicable.
One key determinant of the quality of a measurement with a volumetric pipet is the tolerance -- the accuracy of the device as guaranteed by the manufacturer. The tolerance may be shown on the instrument; if not, it can be obtained from the catalog or other reference source.
There is no necessary relationship between the tolerance and measurement error. However, it turns out that these instruments have been designed so that the tolerance is close to the typical measurement error. Thus, as an approximation, but a useful one, one can treat the stated tolerance as the measurement error. As a rule of thumb, high quality ("Class A") volumetric glassware will give 4 Significant Digits measurements. (In contrast, ordinary glassware will give about 3 Significant Digits at best.) Of course, this assumes that the instrument is being used by trained personnel. In serious work, one would take care to measure actual experimental errors.
Rounding: What to do with a final 5
There are two points to be made here. The first is to make sure that the final 5 really is a final 5. And then, if it is, what to do.
Is the final 5 really a final 5? This might seem to be simple enough, but with common calculators it is easy to be misled. Calculators know nothing about Significant Digits; how many digits they display depends on various things, including how you set them. It is easy for a calculator to mislead you about a final 5. For example, imagine that the true result of a calculation is 8.347, but that the calculator is set to display two decimal places (two digits beyond the decimal point). It will show 8.35. If you want 2 Significant Digits, you would be tempted to round to 8.4. However, that is clearly incorrect, if you look at the complete result 8.347, which should round to 8.3 for 2 Significant Digits. How do you avoid this problem? If you see a final 5 that you want to round off, increase the number of digits displayed before making your decision.
What to do if you really have a final 5. There are two schools of thought on this.
- Some people will suggest that you always round a final 5 up.
- Others will suggest that you round it up and down each half of the time; the usual way to do this is to round a final 5 to make the previous digit an even number. For example, 0.35 becomes 0.4 and 0.65 becomes 0.6.
What should you do? Well, this is really a rather arcane point, not worth much attention. If your instructor prefers a particular way, do it. It really is not a big deal, one way or the other. If you are looking to decide your own preferred approach, I'd suggest you read a bit about what various people suggest, and why. If you just want my opinion, well, I suggest "rounding even".

