Uncertainties in Measurements

All measurements have a degree of uncertainty regardless of precision and accuracy. This is caused by two factors, the limitation of the measuring instrument (systematic error) and the skill of the experimenter making the measurements (random error).

Introduction

The graduated buret in Figure 1 contains a certain amount of water (with yellow dye) to be measured. The amount of water is somewhere between 19 ml and 20 ml according to the marked lines. By checking to see where the bottom of the meniscus lies, referencing the ten smaller lines, the amount of water lies between 19.8 ml and 20 ml. The next step is to estimate the uncertainty between 19.8 ml and 20 ml. Making an approximate guess, the level is less than 20 ml, but greater than 19.8 ml. We then report that the measured amount is approximately 19.9 ml. The graduated cylinder itself may be distorted such that the graduation marks contain inaccuracies providing readings slightly different from the actual volume of liquid present.

Figure 1: A meniscus as seen in a burette of colored water. '20.00 mL' is the correct depth measurement. Click here for a more complete description on buret use, including proper reading. Figure used with permission from Wikipedia.

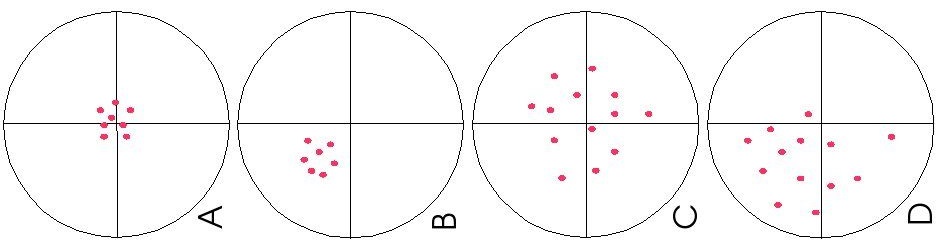
Systematic vs. Random Error

The diagram below illustrates the distinction between systematic and random errors.

Figure 2: Systematic and random errors. Figure used with permission from David DiBiase (Penn State U).

Systematic errors: When we use tools meant for measurement, we assume that they are correct and accurate, however measuring tools are not always right. In fact, they have errors that naturally occur called systematic errors. Systematic errors tend to be consistent in magnitude and/or direction. If the magnitude and direction of the error is known, accuracy can be improved by additive or proportional corrections. Additive correction involves adding or subtracting a constant adjustment factor to each measurement; proportional correction involves multiplying the measurement(s) by a constant.

Random errors: Sometimes called human error, random error is determined by the experimenter's skill or ability to perform the experiment and read scientific measurements. These errors are random since the results yielded may be too high or low. Often random error determines the precision of the experiment or limits the precision. For example, if we were to time a revolution of a steadily rotating turnable, the random error would be the reaction time. Our reaction time would vary due to a delay in starting (an underestimate of the actual result) or a delay in stopping (an overestimate of the actual result). Unlike systematic errors, random errors vary in magnitude and direction. It is possible to calculate the average of a set of measured positions, however, and that average is likely to be more accurate than most of the measurements.

5. Since Tom must rely on the machine for an absorbance reading and it provides consistently different measurements, this is an example of systematic error.
6. The majority of Claire's variation in time can likely be attributed to random error such as fatigue after multiple laps, inconsistency in swimming form, slightly off timing in starting and stopping the stop watch, or countless other small factors that alter lap times. To a much smaller extent, the stop watch itself may have errors in keeping time resulting in systematic error.
7. The researcher's percent error is about 0.62%.
8. This is known as multiplier or scale factor error.
9. This is called an offset or zero setting error.
10. Susan's percent error is -7.62%. This percent error is negative because the measured value falls below the accepted value. In problem 7, the percent error was positive because it was higher than the accepted value.
11. You would first weigh the beaker itself. After obtaining the weight, then you add the graphite in the beaker and weigh it. After obtaining this weight, you then subtract the weight of the graphite plus the beaker minus the weight of the beaker.