10.2: Correlation Function from a Discrete Trajectory
- Page ID
- 107273
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
In practice classical correlation functions in molecular dynamics simulations or single molecule experiments are determined from a time-average over a long trajectory at discretely sampled data points. Let’s evaluate \(C _ {A A} \)for a discrete and finite trajectory in which we are given a series of \(N\) observations of the dynamical variable \(A\) at equally separated time points ti. The separation between time points is \(t _ {i + 1} - t _ {i} = \Delta t\), and the length of the trajectory is \(T = N \Delta t\). Then we have ,
\[C _ {A A} = \frac {1} {T} \sum _ {i , j = 1}^{N} \Delta t A \left( t _ {i} \right) A \left( t _ {j} \right) = \frac {1} {N} \sum _ {i , j = 1}^{N} A _ {i} A _ {j} \label{9.16}\]
where \(A _ {i} = A \left( t _ {i} \right)\). To make this more useful we want to express it as the time interval between points \(\tau = t _ {j} - t _ {i} = ( j - i ) \Delta t\), and average over all possible pairwise products of \(A\) separated by \(\tau\). Defining a new count integer \(n = j -i\), we can express the delay as \(\tau = n \Delta t\). For a finite data set there are a different number of observations to average over at each time interval (n). We have the most pairwise products—\(N\) to be precise—when the time points are equal (ti=tj). We only have one data pair for the maximum delay \(\tau = T\). Therefore, the number of pairwise products for a given delay \(\tau\) is \(N-n\). So we can write Equation \ref{9.16} as
\[C _ {A A} ( \tau ) = C ( n ) = \frac {1} {N - n} \sum _ {i = 1}^{N - n} A _ {i + n} A _ {i} \label{9.17}\]
Note that this expression will only be calculated for positive values of \(n\), for which \(t_j≥t_i\). As an example consider the following calculation for fluctuations in a vibrational frequency \(\omega(t)\), which consists of 32000 consecutive frequencies in units of \(cm^{-1}\) for points separated by 10 femtoseconds, and has a mean value of \(\omega _ {0} = 3244 \mathrm {cm}^{- 1}\). This trajectory illustrates that there are fast fluctuations on femtosecond time scales, but the behavior is seemingly random on 100 picosecond time scales
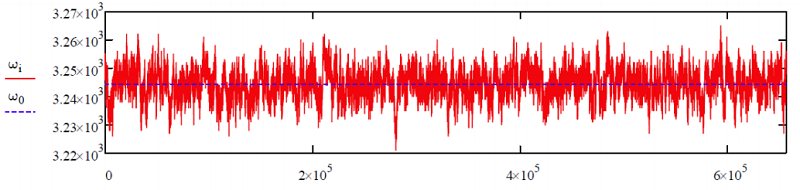
After determining the variation from the mean \(\delta \omega \left( t _ {i} \right) = \omega \left( t _ {i} \right) - \omega 0\), the frequency correlation function is determined from Equation \ref{9.17}, with the substitution \(\delta \omega \left( t _ {i} \right) \rightarrow A _ {i}\).
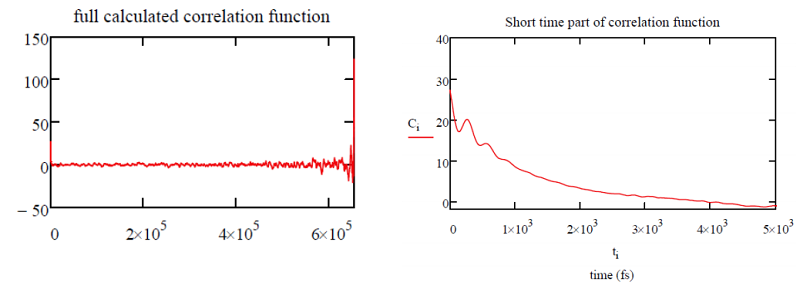
We can see that the correlation function reveals no frequency correlation on the time scale of 104 –105 fs, however a decay of the correlation function is observed for short delays signifying the loss of memory in the fluctuating frequency on the 103 fs time scale. From Equation \ref{9.15}, we find that the correlation time is \(\tau_C = 785\, fs\).


