10.3: Quantum Time-Correlation Functions
- Page ID
- 107274
Quantum correlation functions involve the equilibrium (thermal) average over a product of Hermitian operators evaluated two times. The thermal average is implicit in writing
\[C _ {A A} ( \tau ) = \langle A ( \tau ) A ( 0 ) \rangle.\]
Naturally, this also invokes a Heisenberg representation of the operators, although in almost all cases, we will be writing correlation functions as interaction picture operators
\[A _ {I} (t) = e^{i H _ {0} t} A e^{- i H _ {0} t}.\]
To emphasize the thermal average, the quantum correlation function can also be written as
\[C _ {A A} ( \tau ) = \left\langle \frac {e^{- \beta H}} {Z} A ( \tau ) A ( 0 ) \right\rangle \label{9.18}\]
with \(\beta = \left( k _ {\mathrm {B}} T \right)^{- 1}\). If we evaluate this for a time-independent Hamiltonian in a basis of states n , inserting a projection operator leads to our previous expression
\[C _ {A A} ( \tau ) = \sum _ {n} p _ {n} \langle n | A ( \tau ) A ( 0 ) | n \rangle \label{9.19}\]
with \(p _ {n} = e^{- \beta E _ {n}} / Z\). Given the case of a time-independent Hamiltonian for which we have knowledge of the eigenstates, we can also express the correlation function in the Schrödinger picture as
\[\begin{align} C _ {A A} ( \tau ) &= \sum _ {n} p _ {n} \left\langle n \left| U^{\dagger} ( \tau ) A U ( \tau ) A \right| n \right\rangle \\[4pt] &= \sum _ {n , m} p _ {n} \langle n | A | m \rangle \langle m | A | n \rangle e^{- i \omega _ {m n} \tau} \\[4pt] &= \sum _ {n , m} p _ {n} \left| A _ {m n} \right|^{2} e^{- i \omega _ {m n} \tau} \label{9.20} \end{align}\]
Properties of Quantum Correlation Functions
There are a few properties of quantum correlation functions for Hermitian operators that can be obtained using the properties of the time-evolution operator. First, we can show that correlation functions are stationary:
\[\left.\begin{aligned} \left\langle A (t) A \left( t^{\prime} \right) \right\rangle & = \left\langle U^{\dagger} (t) A ( 0 ) U (t) U^{\dagger} \left( t^{\prime} \right) A ( 0 ) U \left( t^{\prime} \right) \right\rangle \\[4pt] & = \left\langle U \left( t^{\prime} \right) U^{\dagger} (t) A U (t) U^{\dagger} \left( t^{\prime} \right) A \right\rangle \\[4pt] & = \left\langle U^{\dagger} \left( t - t^{\prime} \right) A U \left( t - t^{\prime} \right) A \right\rangle \\[4pt] & = \left\langle A \left( t - t^{\prime} \right) A ( 0 ) \right\rangle \end{aligned} \right. \label{9.21}\]
Similarly, we can show
\[\langle A ( - t ) A ( 0 ) \rangle = \langle A (t) A ( 0 ) \rangle^{*} = \langle A ( 0 ) A (t) \rangle \label{9.22}\]
or in short
\[C _ {A A}^{*} (t) = C _ {A A} ( - t ) \label{9.23}\]
Note that the quantum \(C_{AA}(t)\) is complex. You cannot directly measure a quantum correlation function, but observables are often related to the real or imaginary part of correlation functions.
\[C _ {A A} (t) = C _ {A A}^{\prime} (t) + i C _ {A A}^{\prime \prime} (t) \label{9.24}\]
The real and imaginary parts of \(C_{AA}(t)\) can be separated as
\[\left.\begin{aligned} C _ {A A}^{\prime} (t) & = \frac {1} {2} \left[ C _ {A A} (t) + C _ {A A}^{*} (t) \right] = \frac {1} {2} [ \langle A (t) A ( 0 ) \rangle + \langle A ( 0 ) A (t) \rangle ] \\[4pt] & = \frac {1} {2} \left\langle [ A (t) , A ( 0 ) ] _ {+} \right\rangle \end{aligned} \right. \label{9.25}\]
\[\left.\begin{aligned} C _ {A A}^{\prime \prime} (t) & = \frac {1} {2} \left[ C _ {A A} (t) - C _ {A A}^{*} (t) \right] = \frac {1} {2} [ \langle A (t) A ( 0 ) \rangle - \langle A ( 0 ) A (t) \rangle ] \\[4pt] & = \frac {1} {2} \langle [ A (t) , A ( 0 ) ] \rangle \end{aligned} \right. \label{9.26}\]
Above \([ A , B ] _ {+} \equiv A B + B A\) is the anticommutator. As illustrated below, the real part is even in time, and can be expanded as Fourier series in cosines, whereas the imaginary part is odd, and can be expanded in sines. We will see later that the magnitude of the real part grows with temperature, but the imaginary does not. At 0 K, the real and imaginary components have equal amplitudes, but as one approaches the high temperature or classical limit, the real part dominates the imaginary.
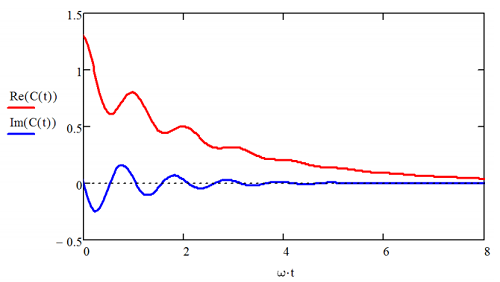
We will also see in our discussion of linear response that \(C'_{AA}\) and \(C''_{AA}\) are directly proportional to the step response function \(S\) and the impulse response function \(R\), respectively. \(R\) describes how a system is driven away from equilibrium by an external potential, whereas \(S\) describes the relaxation of the system to equilibrium when a force holding it away from equilibrium is released. Classically, the two are related by \(R \propto \partial S / \partial t\).
Since time and frequency are conjugate variables, we can also define a spectral or frequency-domain correlation function by the Fourier transformation of the TCF. The Fourier transform and its inverse are defined as
\[ \begin{align} \tilde {C} _ {A A} ( \omega ) &= \tilde {\mathcal {F}} \left[ C _ {A A} (t) \right] \\[4pt] &= \int _ {- \infty}^{+ \infty} \mathrm {e}^{i \omega t} C _ {A A} (t) \,d t \label{9.27} \end{align}\]
\[\begin{align} C _ {A A} (t) &= \tilde {\mathcal {F}}^{- 1} \left[ \tilde {C} _ {A A} ( \omega ) \right] \\[4pt] &= \frac {1} {2 \pi} \int _ {- \infty}^{+ \infty} \mathrm {e}^{- i \omega t} \tilde {C} _ {A A} ( \omega ) \,d \omega \label{9.28} \end{align}\]
Examples of the frequency-domain correlation functions are shown below.
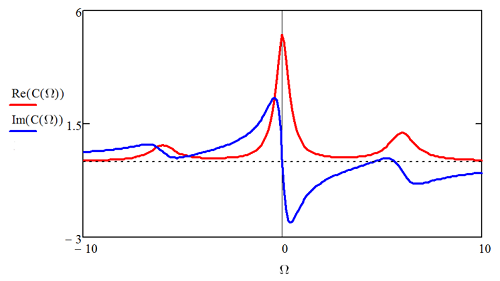
For a time-independent Hamiltonian, as we might have in an interaction picture problem, the Fourier transform of the TCF in Equation \ref{9.20} gives
\[\tilde {C} _ {A A} ( \omega ) = \sum _ {n , m} p _ {n} \left| A _ {m n} \right|^{2} \delta \left( \omega - \omega _ {m n} \right) \label{9.29}\]
This expression looks very similar to the Golden Rule transition rate from first-order perturbation theory. In fact, the Fourier transform of time-correlation functions evaluated at the energy gap gives the transition rate between states that we obtain from first-order perturbation theory. Note that this expression is valid whether the initial states \(n\) are higher or lower in energy than final states \(m\), and accounts for upward and downward transitions. If we compare the ratio of upward and downward transition rates between two states \(i\) and \(j\), we have
\[\frac {\tilde {C} _ {A A} \left( \omega _ {i j} \right)} {\tilde {C} _ {A A} \left( \omega _ {j i} \right)} = \frac {p _ {j}} {p _ {i}} = e^{\beta E _ {j}} \label{9.30}\]
This is one way of showing the principle of detailed balance, which relates upward and downward transition rates at equilibrium to the difference in thermal occupation between states:
\[\tilde {C} _ {A A} ( \omega ) = e^{\beta \hbar \omega} \tilde {C} _ {A A} ( - \omega ) \label{9.31}\]
This relationship together with a Fourier transform of Equation \ref{9.23} allows us to obtain the real and imaginary components using
\[\tilde {C} _ {A A} ( \omega ) \pm \tilde {C} _ {A A} ( - \omega ) = \left( 1 \pm e^{- \beta \hbar \omega} \right) \tilde {C} _ {A A} ( \omega ) \label{9.32}\]
\[\tilde {C} _ {A A}^{\prime} ( \omega ) = \tilde {C} _ {A A} ( \omega ) \left( 1 + e^{- \beta \hbar \omega} \right) \label{9.33}\]
\[\tilde {C} _ {A A}^{\prime \prime} ( \omega ) = \tilde {C} _ {A A} ( \omega ) \left( 1 - e^{- \beta \hbar \omega} \right) \label{9.34}\]


