2.2: Exponential Operators Again
- Page ID
- 107217
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Throughout our work, we will make use of exponential operators of the form \(\hat {T} = e^{- i \hat {A}}\) We will see that these exponential operators act on a wavefunction to move it in time and space. Of particular interest to us is the time-propagator or time-evolution operator \(\hat {U} = e^{- i \hat {H} t / h},\) which propagates the wavefunction in time. Note the operator \(\hat {T}\) is a function of an operator, \(f(\hat{A})\). A function of an operator is defined through its expansion in a Taylor series, for instance
\[\hat {T} = e^{- i \hat {A}} = \sum _ {n = 0}^{\infty} \frac {( - i \hat {A} )^{n}} {n !} = 1 - i \hat {A} - \frac {\hat {A} \hat {A}} {2} - \cdots \label{1.13}\]
Since we use them so frequently, let’s review the properties of exponential operators that can be established with Equation \ref{1.13}. If the operator \(\hat{A}\) is Hermitian, then \(\hat {T} = e^{- i \hat {A}}\) is unitary, i.e., \(\hat {T}^{\dagger} = \hat {T}^{- 1}\). Thus the Hermitian conjugate of \(\hat{T}\) reverses the action of \(\hat{T}\). For the time-propagator \(\hat{U}\), \(U^{†}\) is often referred to as the time-reversal operator.
The eigenstates of the operator \(\hat{A}\) also are also eigenstates of \(f(\hat{A})\), and eigenvalues are functions of the eigenvalues of \(\hat{A}\). Namely, if you know the eigenvalues and eigenvectors of \(\hat{A}\), i.e., \(\hat {A} \varphi _ {n} = a _ {n} \varphi _ {n}\), you can show by expanding the function that
\[f ( \hat {A} ) \varphi _ {n} = f \left( a _ {n} \right) \varphi _ {n} \label{1.14}\]
Our most common application of this property will be to exponential operators involving the Hamiltonian. Given the eigenstates \(\varphi _ {n}\), then \(\hat {H} | \varphi _ {n} \rangle = E _ {n} | \varphi _ {n} \rangle\) implies
\[e^{- i \hat {H} t / \hbar} | \varphi _ {n} \rangle = e^{- i E _ {n} t / \hbar} | \varphi _ {n} \rangle \label{1.15}\]
Just as \(\hat {U} = e^{- i \hat {H} t / h}\) is the time-evolution operator, which displaces the wavefunctionin time, \(\hat {D} _ {x} = e^{- i \hat {p} _ {x} x / \hbar}\) is the spatial displacement operator that moves \(\psi\) along the \(x\) coordinate. If we define \(\hat {D} _ {x} ( \lambda ) = e^{- i \hat {p} _ {x} \lambda / h},\) then the action of is to displace the wavefunction by an amount \(\lambda\)
\[| \psi ( x - \lambda ) \rangle = \hat {D} _ {x} ( \lambda ) | \psi (x) \rangle \label{1.16}\]
Also, applying \(\hat {D} _ {x} ( \lambda )\) to a position operator shifts the operator by \(\lambda\)
\[\hat {D} _ {x}^{\dagger} \hat {x} \hat {D} _ {x} = \hat {x} + \lambda \label{1.17}\]
Thus \(e^{- i \hat {p} _ {x} \lambda / h} | x \rangle\) is an eigenvector of \(\hat{x}\) with eigenvalue \(x + \lambda\) instead of \(x\). The operator \(\hat {D} _ {x} = e^{- i \hat {p} _ {x} \lambda / \hbar}\) is a displacement operator for \(x\) position coordinates. Similarly, \(\hat {D} _ {y} = e^{- i \hat {p} _ {y} \lambda / \hbar}\) generates displacements in \(y\) and \(\hat{D}_z\) in \(z\). Similar to the time-propagator \(\hat{U}\), the displacement \(hta{D}\) operator must be unitary, since the action of must leave the system unchanged. That is if \(\hat{D}\) shifts the system to from , then shifts the system from \(x\) back to \(x_0\).
We know intuitively that linear displacements commute. For example, if we wish to shift a particle in two dimensions, \(x\) and \(y\), the order of displacement does not matter. We end up at the same position. These displacement operators commute, as expected from \([\hat{p}_x,\hat{p}_y] = 0\)
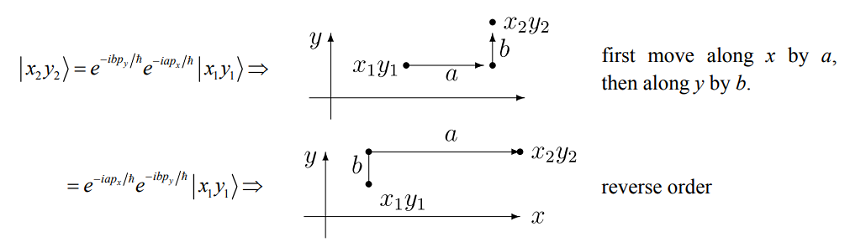
Similar to the displacement operator, we can define rotation operators that depend on the angular momentum operators, \(L_x\), \(L_y\), and \(L_z\). For instance, \(\hat {R} _ {x} ( \phi ) = e^{- i \phi L _ {x} / \hbar}\) gives a rotation by angle \(\phi\) about the x-axis. Unlike linear displacement, rotations about different axes do not commute. For example, consider a state representing a particle displaced along the z-axis, \(| \mathrm {Z} 0 \rangle\). Now the action of two rotations \(\hat{R}_x\) and \(\hat{R}_y\) by an angle of \(\pi/2\) on this particle differs depending on the order of operation.
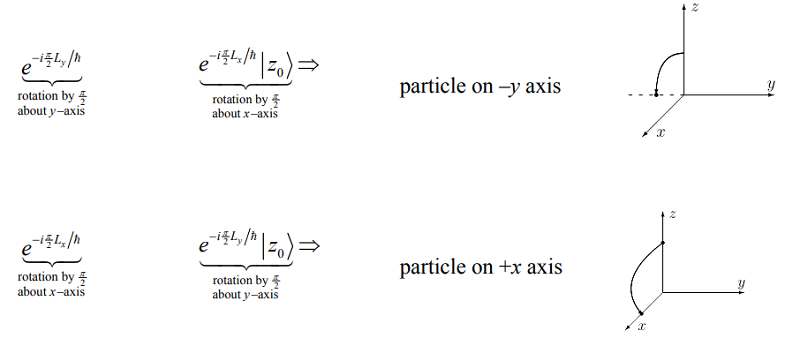
The results of these two rotations taken in opposite order differ by a rotation about the z–axis. Thus, because the rotations about different axes do not commute, we must expect the angular momentum operators, which generate these rotations, not to commute. Indeed, we know that \([L_x,L_y] = i\hbar L_z\) where the commutator of rotations about the x and y axes is related by a z-axis rotation. As with rotation operators, we will need to be careful with time-propagators to determine whether the order of time-propagation matters. This, in turn, will depend on whether the Hamiltonians at two points in time commute.
Useful Properties of Exponential Operator
Finally, it is worth noting some relationships that are important in evaluating the action of exponential operators:
- The Baker–Hausdorff relationship: \[\left. \begin{array} {r l} {\exp ( i \hat {G} \lambda ) \hat {A} \exp ( - i \hat {G} \lambda ) = \hat {A} + i \lambda [ \hat {G} , \hat {A} ] + \left( \frac {i^{2} \lambda^{2}} {2 !} \right) [ \hat {G} , [ \hat {G} , \hat {A} ] ] + \ldots} \\ {+ \left( \frac {i^{n} \lambda^{n}} {n !} \right) [ \hat {G} , [ \hat {G} , [ \hat {G} , \hat {A} ] ] ] \ldots ]} & {+ \dots} \end{array} \right. \label{1.18}\]
- If \(\hat {A}\) and \(\hat {B}\) do not commute, but \([ \hat {A} , \hat {B} ]\) commutes with \(\hat {A}\) and \(\hat {B}\), then \[e^{\hat {A} + \hat {B}} = e^{\hat {A}} e^{\hat {B}} e^{- \frac {1} {2} [ \hat {A} , \hat {B} ]}\label{1.19}\]
- \[e^{\hat {A}} e^{\hat {B}} = e^{\hat {B}} e^{\hat {A}} e^{- [ \hat {B} , \hat {A} ]} \label{1.19B}\]
Time-Evolution Operator
Since the TDSE is deterministic and linear in time, we can define an operator that describes the dynamics of the wavefunction:
\[\psi (t) = \hat {U} \left( t , t _ {0} \right) \psi \left( t _ {0} \right) \label{1.20}\]
\(U\) is is the time-propagator or time-evolution operator that evolves the quantum system as a function of time. It represents the solution to the time-dependent Schrödinger equation. To investigate its form we consider the TDSE for a time-independent Hamiltonian:
\[\frac {\partial} {\partial t} \psi ( \overline {r} , t ) + \frac {i \hat {H}} {\hbar} \psi ( \overline {r} , t ) = 0 \label{1.21}\]
To solve this, we will define an exponential operator \(\hat {T} = \exp ( - i \hat {H} t / \hbar )\), which is defined through its expansion in a Taylor series:
\[ \begin{align} \hat {T} &= \exp ( - i \hat {H} t / \hbar ) \\[4pt] &= 1 - \frac {i \hat {H} t} {\hbar} + \frac {1} {2 !} \left( \frac {i \hat {H} t} {\hbar} \right)^{2} - \cdots \end{align} \label{1.22}\]
You can also confirm from the expansion that \(\hat {T}^{- 1} = \exp ( i \hat {H} t / \hbar ),\) noting that \(\hat{H}\) is Hermitian and commutes with \(\hat{T}\). Multiplying Equation \ref{1.21} from the left by \(\hat {T}^{- 1}\), we can write
\[\frac {\partial} {\partial t} \left[ \exp \left( \frac {i \hat {H} t} {\hbar} \right) \psi ( \overline {r} , t ) \right] = 0 \label{1.23}\]
and integrating \(t _ {0} \rightarrow t\), we get
\[\exp \left( \frac {i \hat {H} t} {\hbar} \right) \psi ( \overline {r} , t ) - \exp \left( \frac {i \hat {H} t _ {0}} {\hbar} \right) \psi \left( \overline {r} , t _ {0} \right) = 0 \label{1.24}\]
\[\psi ( \overline {r} , t ) = \exp \left( \frac {- i \hat {H} \left( t - t _ {0} \right)} {\hbar} \right) \psi \left( \overline {r} , t _ {0} \right) \label{1.25}\]
So, comparing to Equation \ref{1.20}, we see that the time-propagator is
\[\hat {U} \left( t , t _ {0} \right) = \exp \left( \frac {- i \hat {H} \left( t - t _ {0} \right)} {\hbar} \right) \label{1.26}\]
For the time-independent Hamiltonian for which we know the eigenstates \(\phi_n\) and eigenvalues \(E_n\), we can express this in a practical form using Equation \ref{1.14}
\[\psi _ {n} ( \overline {r} , t ) = e^{- i E _ {n} \left( t - t _ {0} \right) / \hbar} \psi _ {n} \left( \overline {r} , t _ {0} \right) \label{1.27}\]
Alternatively, if we substitute the projection operator (or identity relationship)
\[\sum _ {n} | \varphi _ {n} \rangle \langle \varphi _ {n} | = 1 \label{1.28}\]
into Equation \ref{1.26}, we see
\[\begin{align} \hat {U} \left( t , t _ {0} \right) &= e^{- i \hat {H} \left( t - t _ {0} \right) / \hbar} \sum _ {n} | \varphi _ {n} \rangle \langle \varphi _ {n} | \\[4pt] &= \sum _ {n} e^{- i \omega _ {n} \left( t - t _ {0} \right)} | \varphi _ {n} \rangle \langle \varphi _ {n} | \end{align}\]
\[\omega _ {n} = \frac {E _ {n}} {\hbar}\]
So now we can write our time-developing wave-function as
\[\begin{align} | \psi _ {n} ( \overline {r} , t ) \rangle & = | \varphi _ {n} \rangle \sum _ {n} e^{- i \omega _ {n} \left( t - t _ {0} \right)} \left\langle \varphi _ {n} | \psi _ {n} \left( \overline {r} , t _ {0} \right) \right\rangle \\ & = \sum _ {n} e^{- i \omega _ {n} \left( t - t _ {0} \right)} c _ {n} \\ & = \sum _ {n} c _ {n} (t) | \varphi _ {n} \rangle \end{align} \label{1.30}\]
As written in Equation \ref{1.20}, we see that the time-propagator \(\hat {U} \left( t , t _ {0} \right)\), acts to the right (on kets) to evolve the system in time. The evolution of the conjugate wavefunctions (bras) is under the Hermitian conjugate of \(\hat {U} \left( t , t _ {0} \right)\), acting to the left:
\[\langle \psi (t) | = \langle \psi \left( t _ {0} \right) | \hat {U}^{\dagger} \left( t , t _ {0} \right) \label{1.31}\]
From its definition as an expansion and recognizing \(\hat{H}\) as Hermitian, you can see that
\[\hat {U}^{\dagger} \left( t , t _ {0} \right) = \exp \left[ \frac {i \hat {H} \left( t - t _ {0} \right)} {\hbar} \right] \label{1.32}\]
Noting that \(\hat{U}\) is unitary, \(\hat {U}^{\dagger} = \hat {U}^{- 1}\), we often refer to \(\hat {U}^{\dagger}\) as the time reversal operator.


