2.3: Two-Level Systems
- Page ID
- 107218
Let’s use the time-propagator in a model calculation that we will refer to often. It is common to reduce or map quantum problems onto a two level system (2LS). We will pick the most important states for our problem and find strategies for discarding or simplifying the influence of the remaining degrees of freedom. Consider a 2LS with two unperturbed or “zeroth order” states \(| \varphi _ {a} \rangle\) and \(| \varphi _ {b} \rangle\) with energies \( {\varepsilon} _ {a}\) and \( {\varepsilon} _ {b}\), which are described by a zero-order Hamiltonian \(H_0\):
\[\begin{align} \hat {H} _ {0} &= | \varphi _ {a} \rangle \varepsilon _ {a} \left\langle \varphi _ {a} | + | \varphi _ {b} \right\rangle \varepsilon _ {b} \langle \varphi _ {b} | \\[4pt] &= \left( \begin{array} {l l} {\varepsilon _ {a}} & {0} \\[4pt] {0} & {\varepsilon _ {b}} \end{array} \right) \label{1.33} \end{align}\]
These states interact through a coupling \(V\) of the form
\[\begin{align} \hat {V} &= | \varphi _ {a} \rangle V _ {a b} \left\langle \varphi _ {b} | + | \varphi _ {b} \right\rangle V _ {b a} \langle \varphi _ {a} | \\[4pt] &= \left( \begin{array} {l l} {0} & {V _ {a b}} \\[4pt] {V _ {b a}} & {0} \end{array} \right) \label{1.34} \end{align}\]
The full Hamiltonian for the two coupled states is \(\hat{H}\):
\[\begin{align} \hat {H} & = \hat {H} _ {0} + \hat {V} \\[4pt] & = \left( \begin{array} {c c} {\varepsilon _ {a}} & {V _ {a b}} \\[4pt] {V _ {b a}} & {\varepsilon _ {b}} \end{array} \right) \label{1.35} \end{align} \]
The zero-order states are \(| \varphi _ {a} \rangle\) and \(| \varphi _ {b} \rangle\). The coupling mixes these states, leading to two eigenstates of \(\hat{H}\), \(| \varphi _ {+} \rangle\) and \(| \varphi _ {-} \rangle\), with corresponding energy eigenvalues \( {\varepsilon} _ {+}\) and \( {\varepsilon} _ {-}\), respectively.
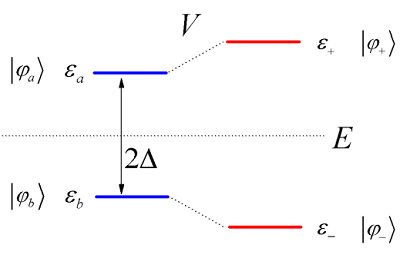
We will ask: If we prepare the system in state \(| \varphi _ {a} \rangle\), what is the time-dependent probability of observing it in \(| \varphi _ {b} \rangle\)? Since \(| \varphi _ {a} \rangle\) and \(| \varphi _ {b} \rangle\) are not eigenstates of \(\hat{H}\), and since our time-propagation will be performed in the eigenbasis using Equation \ref{1.29}, we will need to find the transformation between these bases.
We start by searching for the eigenvalues of the Hamiltonian (Equation \ref{1.35}). Since the Hamiltonian is Hermitian, (\(H _ {i j} = H _ {j i}^{*}\)), we write
\[V _ {a b} = V _ {b a}^{*} = V e^{- i \varphi} \label{1.36}\]
\[\hat {H} = \left( \begin{array} {c c} {\varepsilon _ {a}} & {V e^{- i \varphi}} \\[4pt] {V e^{+ i \varphi}} & {\varepsilon _ {b}} \end{array} \right) \label{1.37}\]
Often the couplings we describe are real, and we can neglect the phase factor \(\phi\). Now we define variables for the mean energy and energy splitting between the uncoupled states
\[E = \frac {\varepsilon _ {a} + \varepsilon _ {b}} {2}\]
\[\Delta = \frac {\varepsilon _ {a} - \varepsilon _ {b}} {2} \label{1.39}\]
We can then obtain the eigenvalues of the coupled system by solving the secular equation
\[\operatorname {det} ( H - \lambda I ) = 0\]
giving
\[\varepsilon _ {\pm} = E \pm \Omega \label{1.41}\]
Here I defined another variable
\[\Omega = \sqrt {\Delta^{2} + V^{2}} \label{1.42}\]
To determine the eigenvectors of the coupled system \(| \varphi _ {\pm} \rangle\), it proves to be a great simplification to define a mixing angle \(\theta\) that describes the relative magnitude of the coupling relative to the zero-order energy splitting through
\[\tan 2 \theta = \frac {V} {\Delta} \label{1.43}\]
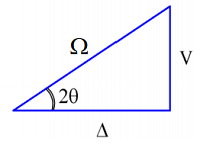
We see that the mixing angle adopts values such that \(0 \leq \theta \leq \pi / 4\). Also, we note that
\[\sin 2 \theta = V / \Omega \label{1.44}\]
\[\cos 2 \theta = \Delta / \Omega \label{1.45}\]
In this representation the Hamiltonian (Equation \ref{1.37}) becomes
\[\hat {H} = E \overline {I} + \Delta \left( \begin{array} {l l} {1} & {\tan 2 \theta e^{- i \varphi}} \\[4pt] {\tan 2 \theta e^{+ i \varphi}} & {- 1} \end{array} \right) \label{1.46}\]
and we can express the eigenvalues as
\[\varepsilon _ {\pm} = E \pm \Delta \sec 2 \theta \label{1.47}\]
Next we want to find \(S\), the transformation that diagonalizes the Hamiltonian and which transforms the coefficients of the wavefunction from the zero-order basis to the eigenbasis. The eigenstates can be expanded in the zero-order basis in the form
\[| \varphi _ {\pm} \rangle = c _ {a} | \varphi _ {a} \rangle + c _ {b} | \varphi _ {b} \rangle \label{1.48}\]
So that the transformation can be expressed in matrix form as
\[\left( \begin{array} {l} {\varphi _ {+}} \\[4pt] {\varphi _ {-}} \end{array} \right) = S \left( \begin{array} {l} {\varphi _ {a}} \\[4pt] {\varphi _ {b}} \end{array} \right)\label{1.49}\]
To find \(S\), we use the Schrödinger equation \(\hat {H} | \varphi _ {\pm} \rangle = \varepsilon _ {\pm} | \varphi _ {\pm} \rangle\)
substituting Equation \ref{1.48}. This gives
\[S = \left( \begin{array} {l l} {\cos \theta} & {e^{- i \varphi / 2}} & {\sin \theta} & {e^{i \varphi / 2}} \\[4pt] {- \sin \theta} & {e^{- i \varphi / 2}} & {\cos \theta} & {e^{i \varphi / 2}} \end{array} \right) \label{1.50}\]
Note that \(S\) is unitary since \(S^{\dagger} = S^{- 1}\) and \(\left( S^{T} \right)^{*} = S^{- 1}\). Also, the eigenbasis is orthonormal:
\[\left\langle \varphi _ {+} | \varphi _ {+} \right\rangle + \left\langle \varphi _ {-} | \varphi _ {-} \right\rangle = 1.\]
Now, let’s examine the eigenstates in two limits:
- Weak coupling (\(| {V} / \Delta | \ll 1\)). Here \(\theta \approx 0\), and \(| \varphi _ {+} \rangle\) corresponds to \(| \varphi _ {a} \rangle\) weakly perturbed by the \(V_{ab}\) interaction. \(| \varphi _ {-} \rangle\) corresponds to \(| \varphi _ {b} \rangle\). In another way, as \(\theta \rightarrow 0\), we find \[| \varphi _ {+} \rangle \rightarrow | \varphi _ {a} \rangle\] and \[| \varphi _ {-} \rangle \rightarrow | \varphi _ {b} \rangle.\]
- Strong coupling (\(| V / \Delta | \gg 1\)). In this limit \(\theta = \pi / 4\), and the \(a/b\) basis states are indistinguishable. The eigenstates are symmetric and antisymmetric combinations: \[| \varphi _ {\pm} \rangle = \frac {1} {\sqrt {2}} ( | \varphi _ {b} \rangle \pm | \varphi _ {a} \rangle ) \label{1.51}\] Note from Equation \ref{1.50} that the sign of \(V\) dictates whether \(| \varphi _ {+} \rangle\) or \(| \varphi _ {-} \rangle\) corresponds to the symmetric or antisymmetric eigenstate. For negative \(V \gg \Delta\), \(\theta = - \pi / 4\), and the correspondence in Equation \ref{1.51} changes to \(\mp\).
We can schematically represent the energies of these states with the following diagram. Here we explore the range of \( {E} _ {\pm}\) available given a fixed coupling \(V\) and varying the splitting \(\Delta\).
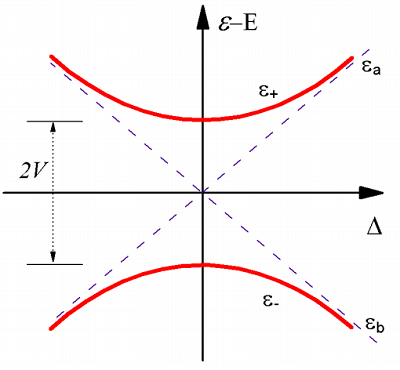
This diagram illustrates an avoided crossing effect. The strong coupling limit is equivalent to a degeneracy point (\(\Delta = 0\)) between the states \(| \varphi _ {a} \rangle\) and \(| \varphi _ {b} \rangle\). The eigenstates completely mix the unperturbed states, yet remain split by the strength of interaction \(2V\). We will return to the discussion of avoided crossings when we describe potential energy surfaces and the adiabatic approximation, where the dependence of \(V\) and \(\Delta\) on position \(R\) must be considered.
Now we can turn to describing dynamics. The time evolution of this system is given by the time-propagator
\[U (t) = | \varphi _ {+} \rangle e^{- i \omega , t} \left\langle \varphi _ {+} | + | \varphi _ {-} \right\rangle e^{- i \omega t} \langle \varphi _ {-} | \label{1.52}\]
where \(\omega _ {\pm} = \varepsilon _ {\pm} / \hbar\). Since \(\varphi _ {a}\) and \(\varphi _ {b}\) are not the eigenstates, preparing the system in state \(\varphi _ {a}\) will lead to time evolution! Let’s prepare the system so that it is initially in \(\varphi _ {a}\).
\[| \psi ( 0 ) \rangle = | \varphi _ {a} \rangle \label{1.53} \nonumber\]
Evaluating the time-dependent amplitudes of initial and final states with the help of \(S\), we find
\[\begin{align*} c _ {a} (t) & = \left\langle \varphi _ {a} | U (t) | \varphi _ {a} \right\rangle \\[4pt] & = e^{- i E t} \left[ \cos^{2} \theta e^{i \Omega _ {R} t} + \sin^{2} \theta e^{- i \Omega _ {R} t} \right] \label{1.54} \\[4pt] c _ {b} (t) & = \left\langle \varphi _ {b} | U (t) | \varphi _ {a} \right\rangle \\[4pt] & = 2 \sin \theta \cos \theta e^{- i E t} \sin \Omega _ {R} t \label{1.55} \end{align*}\]
So, what is the probability that it is found in state \(| \varphi _ {b} \rangle\) at time \(t\)?
\[\begin{aligned} P _ {b a} (t) & = \left| c _ {b} (t) \right|^{2} \\[4pt] & = \frac {V^{2}} {V^{2} + \Delta^{2}} \sin^{2} \Omega _ {R} t \end{aligned} \label{1.56}\]
where
\[\Omega _ {R} = \frac {1} {\hbar} \sqrt {\Delta^{2} + V^{2}} \label{1.57}\]
\(\Omega _ {R}\), the Rabi Frequency, represents the frequency at which probability amplitude oscillates between \(\varphi _ {a}\) and \(\varphi _ {b}\) states.
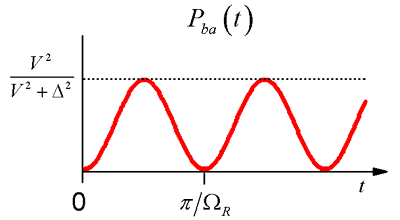
Notice for the weak coupling limit (\(V \rightarrow 0\)), \(\varphi _ {\pm} \rightarrow \varphi _ {a , b}\) (the eigenstates resemble the stationary states), and the time-dependence disappears. In the strong coupling limit (\(V \gg \Delta\)), amplitude is exchanged completely between the zero-order states at a rate given by the coupling: \(\Omega _ {R} \rightarrow V / \hbar\). Even in this limit it takes a finite amount of time for amplitude to move between states. To get \(P=1\) requires a time \(\tau\):
\[\tau = \pi / 2 \Omega _ {R} = \hbar \pi / 2 V. \nonumber\]
Readings
- Cohen-Tannoudji, C.; Diu, B.; Lalöe, F., Quantum Mechanics. Wiley-Interscience: Paris, 1977; pp. 405-420.
- Liboff, R. L., Introductory Quantum Mechanics. Addison-Wesley: Reading, MA, 1980; p. 77.
- Mukamel, S., Principles of Nonlinear Optical Spectroscopy. Oxford University Press: New York, 1995; Ch. 2.
- Sakurai, J. J., Modern Quantum Mechanics, Revised Edition. Addison-Wesley: Reading, MA, 1994.


