24.7: The Electronic Partition Function of an Ideal Gas
- Page ID
- 152805
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Our quantum-mechanical model for a diatomic molecule takes the zero of energy to be the infinitely separated atoms at rest—that is, with no kinetic energy. The electrical interactions among the nuclei and electrons are such that, as the atoms approach one another, a bond forms and the energy of the two-atom system decreases. At some inter-nuclear distance, the energy reaches a minimum; at shorter inter-nuclear distances, the repulsive interactions between nuclei begin to dominate, and the energy increases. We can use quantum mechanics to find the wavefunction and energy of the molecule when the nuclei are separated to any fixed distance. By repeating the calculation at a series of inter-nuclear distances, we can find the distance at which the molecular energy is a minimum. We take this minimum energy as the electronic energy of the molecule, and the corresponding inter-nuclear distance as the bond length. This is the energy of the lowest electronic state of the molecule. The lowest electronic state is called the ground state.
Excited electronic states exist, and their energies can be estimated from spectroscopic measurements or by quantum mechanical calculation. For most molecules, these excited electronic states are at much higher energy than the ground state. When we compare the terms in the electronic partition function, we see that
\[{\mathrm{exp} \left({-{\epsilon }_{e,1}}/{kT}\right)\ }\gg {\mathrm{exp} \left({-{\epsilon }_{e,2}}/{kT}\right)\ } \nonumber \]
The term for any higher energy level is insignificant compared to the term for the ground state. The electronic partition function becomes just
\[z_e=g_1{\mathrm{exp} \left({-{\epsilon }_{e,1}}/{kT}\right)\ } \nonumber \]
The ground-state degeneracy, \(g_1\), is one for most molecules. For unusual molecules the ground-state degeneracy can be greater; for molecules with one unpaired electron, it is two.
The energy of the electronic ground state that we obtain by direct quantum mechanical calculation includes the energy effects of the motions of the electrons and the energy effects from the electrical interactions among the electrons and the stationary nuclei. Because we calculate it for stationary nuclei, the electronic energy does not include the energy of nuclear motions. The ground state electronic energy is the energy released when the atoms come together from infinite separation to a state in which they are at rest at the equilibrium inter-nuclear separation. This is just minus one times the work required to separate the atoms to an infinite distance, starting from the inter-nuclear separation with the smallest energy. On a graph of electronic (or potential) energy versus inter-nuclear distance, the ground state energy is just the depth of the energy well measured from the top down \(\left({\epsilon }_{e,1}<0\right)\). The work required to separate one mole of these molecules into their constituent atoms is called the equilibrium dissociation energy, and conventionally given the symbol \(D_e\). These definitions mean that \(D_e>0\) and \(D_e=-\overline{N}{\epsilon }_{e,1}\).
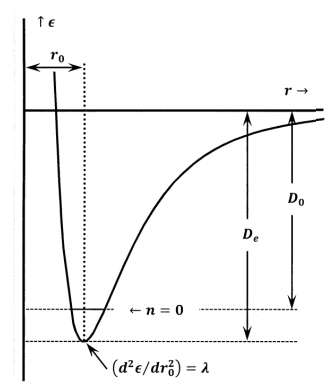
In practice, the energy of the electronic ground state is often estimated from spectroscopic measurements. By careful study of its spectra, it is possible to find out how much energy must be added, as a photon, to cause a molecule to dissociate into atoms. Expressed per mole, this energy is called the spectroscopic dissociation energy, and it is conventionally given the symbol \(D_0\). These spectroscopic measurements involve the absorption of photons by real molecules. Before they absorb the photon, these molecules already have energy in the form of vibrational and rotational motions. So the real molecules that are involved in any spectroscopic measurement have energies that are greater than the energies of the hypothetical motionless-atom molecules at the bottom of the potential energy well. This means that less energy is required to separate the real molecule than is required to separate the hypothetical molecule at the bottom of the well. For any molecule, \(D_e\mathrm{>}D_0\).
To have the lowest possible energy, a real molecule must be in its lowest rotational and lowest vibrational energy levels. As turns out, a molecule can have zero rotational energy, but its vibrational energy can never be zero. In Section 24.8 we review the harmonic oscillator approximation. In its lowest vibrational energy level \(\left(n=0\right)\), a diatomic molecule’s minimum vibrational energy is \({h\nu }/{\mathrm{2}}\). \(D_0\) and \(\nu\) can be estimated from spectroscopic experiments. We estimate
\[{\epsilon }_{e,1}=-\frac{D_e}{\overline{N}}=-\left(\frac{D_0}{\overline{N}}+\frac{h\nu }{2}\right) \nonumber \]
and the molecular electronic partition function becomes
\[z_e=g_1{\mathrm{exp} \left(\frac{D_0}{\overline{N}kT}+\frac{h\nu }{2kT}\right)\ } \nonumber \]
or
\[z_e=g_1{\mathrm{exp} \left(\frac{D_0}{RT}+\frac{h\nu }{2kT}\right)\ } \nonumber \]


