13.8: Equilibrium When A Component is Also Present as A Condensed Phase
- Page ID
- 152383
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Suppose that the very large equilibrium system with ideal gas components at pressures \(P_A\), \(P_B\), \(P_C\), and \(P_D\), also contains a quantity of liquid \(A\). (For the present, we assume that this is pure liquid \(A\); components \(B\), \(C\), and \(D\) are insoluble in liquid \(A\).) If this augmented system is at equilibrium, we know that liquid \(A\) is in phase equilibrium with ideal gas \(A\) at pressure \(P_A\). That is, \(P_A\) is the vapor pressure of liquid \(A\) at the fixed temperature that we are considering, and the Gibbs free energy change for converting liquid \(A\) to its ideal gas at \(P_A\) is zero. As long as the liquid is in phase equilibrium with its ideal gas, the relationship between the ideal gas partial pressures and the standard Gibbs free energy change for the reaction is not affected by the presence of the liquid. These same considerations apply when the very large equilibrium system contains both ideal gas \(A\) and solid \(A\), so long as the equilibrium sublimation pressure is equal to the partial pressure of ideal gas A, \(P_A\).
Now, let us suppose that substance \(A\) is a non-volatile liquid or solid. In this case, we may not be able to measure the standard Gibbs free energy of formation of ideal gas \(A\). From a practical standpoint, this is an important consideration; if we cannot find the standard Gibbs free energy of formation of the ideal gas, we cannot use it to calculate equilibrium constants. From a theoretical standpoint, it is less crucial; we can reasonably imagine that any substance has a finite vapor pressure at any temperature, even if the value is much too small to measure experimentally. We can reason about the relationship of the equilibrium vapor pressure to other quantities whether we can measure it or not.
If substance \(A\) is a non-volatile liquid (or solid) at the temperature of interest, it is useful to modify the cycle introduced in the preceding section. We can find the standard Gibbs free energy of formation for the liquid from thermal measurements, and we can use liquid \(A\) rather than ideal gas \(A\) as the standard state. If \(A\) is non-volatile, it is present in the equilibrium system only as the liquid. For present purposes, we again assume that the other components are insoluble in liquid \(A\); then, the only difference between \(A\) in its standard state and \(A\) in the equilibrium system is that the pressure on \(A\) in its standard state is one bar and the pressure on liquid \(A\) in the equilibrium system is \(P=P_B+P_C+P_D\). Therefore, when \(a\) moles of liquid \(A\) go from their standard state to the equilibrium system, the Gibbs free energy change is
\[{\Delta }_{press}G_A=a\int^P_{P^o}{{\overline{V}}^{\textrm{⦁}}_A}\left(\ell \right)dP \nonumber \]
where \({\overline{V}}^{\textrm{⦁}}_A\left(\ell \right)\) is the molar volume of pure liquid \(A\). When \(a\) moles of liquid \(A\) are produced at the equilibrium pressure from the elements, the Gibbs free energy change is
\[a{\overline{G}}_A\left(\ell ,P\right)=a\ {\Delta }_fG^o\left(A,\ell \right)+a\int^P_{P^o}{{\overline{V}}^{\textrm{⦁}}_A}\left(\ell \right)dP \nonumber \]
In Section 15.3, we give further attention to the value of this integral; for now, let us simply note that it is negligible in essentially all circumstances. These considerations mean that we can modify the left side of the cycle in Figure 5 as indicated in Figure 7.
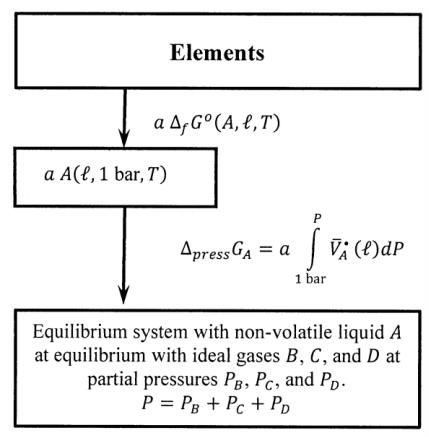
When we sum around the modified cycle in the same manner as before, we find
\[0=a\ {\Delta }_fG^o\left(A,\ell \right)+b\ {\Delta }_fG^o\left(B,P^o\right)-c\ {\Delta }_fG^o\left(C,P^o\right) \nonumber \] \[-d\ {\Delta }_fG^o\left(D,P^o\right)+a\int^P_{P^o}{{\overline{V}}^{\textrm{⦁}}_A}\left(\ell \right)dP+RT{ \ln p^b_B\ } \nonumber \] \[-RT{ \ln p^c_C-RT{ \ln p^d_D\ }\ } \nonumber \]
where we have supplemented our notation to emphasize that \(A\) is a non-volatile liquid while \(B\), \(C\), and\(\ D\) are ideal gases. We continue to use \({\Delta }_rG^o\) to represent the difference between the standard Gibbs free energies of the products and those of the reactants. In the present circumstances, we have
\[{\Delta }_rG^o=\ c\ {\Delta }_fG^o\left(C,P^o\right)+d\ {\Delta }_fG^o\left(D,P^o\right)-a\ {\Delta }_fG^o\left(A,\ell \right)-b\ {\Delta }_fG^o\left(B,P^o\right) \nonumber \]
Taking the value of the integral as zero, our result simplifies to
\[{\Delta }_rG^o=-RT{ \ln \frac{p^c_Cp^d_D}{p^b_B}\ } \nonumber \]
We have again arrived at the conclusion that the “concentration” of a pure solid or liquid can be set equal to unity in the equilibrium constant expression for a reaction in which it participates. When we do so, we must use the Gibbs free energy of formation of the condensed phase in the calculation of \({\Delta }_rG^o\).


