13.3: The Thermodynamics of Mixing Ideal Gases
- Page ID
- 151741
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)When we talk about the thermodynamics of mixing, we have a very particular process in mind. By convention, the process of mixing two gases, call them \(A\) and \(B\), is the process in which the two gases initially occupy separate containers, but are both at a common pressure and temperature. (We denote the common initial pressure by “\(P_0\)”. \(P_0\) is not to be confused with the constant \(P^o\).) The final state after the mixing process is one in which there is a homogeneous mixture of \(A\) and \(B\) at the same temperature as characterized the initial state. The final volume is the sum of the initial volumes. If the gases are ideal, the final pressure is the same as the initial pressure, and the partial pressures are \(P_A={n_ART}/{\left(V_A+V_B\right)}\) and \(P_B={n_BRT}/{\left(V_A+V_B\right)}\).
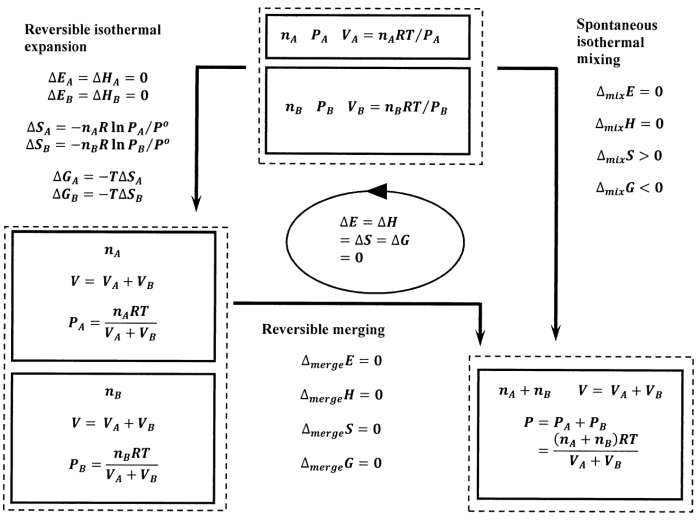
The mixing process is represented by the change on the right side of Figure 1. The gases are always in thermal contact with constant-temperature surroundings. We imagine that we bring the initially separate containers together and then remove the overlapping walls. (Or we can imagine connecting the two containers by a tube—whose volume is negligibly small—that allows the molecules to move from one container to the other.) Molecular diffusion eventually causes the concentration of either gas to be the same in any macroscopic portion of the combined volumes. This diffusive mixing begins as soon as we provide a path for the molecules to move between their containers. Isothermal mixing is a spontaneous process. The reverse process does not occur. Isothermal mixing is irreversible.
Since the temperature is constant and the gases are ideal, the energy of the \(A\) molecules is constant; likewise, the energy of the \(B\) molecules constant. It follows that the energy of a system containing molecules of \(A\) and \(B\) is independent of their concentrations and that the energy of the mixture is the sum of the energies of the separated components. That is, we have \({\Delta }_{mix}E=0\). Since the volume and the pressure of the two-gas system are constant, it follows that \({\Delta }_{mix}\left(PV\right)=0\) and \({\Delta }_{mix}H=0\). Constant volume also means that \(w_{mix}=0\). It follows that \(q_{mix}=0\), and that \({\Delta }_{mix}\hat{S}=0\). Then, because the mixing process is spontaneous, we have \({\Delta }_{mix}S>0\). Finally, since \({\Delta }_{mix}H=0\), we have \({\Delta }_{mix}G=-T{\Delta }_{mix}S<0\). However, in order to calculate the values of \({\Delta }_{mix}S=0\) and \({\Delta }_{mix}G<0\), we must find a reversible path for the state change that occurs during mixing.
The two-step path represented by the changes along the left side and the bottom of Figure 1 is such a reversible path. The first step is simply the reversible isothermal expansion of the separate gases from their initial volumes (\(V_A\) and \(V_B\), respectively) to the common final volume, \(V_A+V_B\). At the end of this step, the two gases are still in separate containers. Reversible isothermal expansion of an ideal gas is a familiar process; for this step, we know:
\[\Delta E_A=\Delta H_A=0 \nonumber \] \[\Delta E_B=\Delta H_B=0 \nonumber \]
\[\Delta S_A=-n_AR \ln \left(P_A/P_0\right)>0 \nonumber \] \[\Delta S_B=-n_BR \ln \left(P_B/P_0\right) > 0 \nonumber \]
\[\Delta G_A=-T\Delta S_A<0 \nonumber \] \[\Delta G_B=-T\Delta S_B<0 \nonumber \]
We call the change along the bottom of the diagram the merging process. The merging process is the isothermal, reversible blending of the separate gas samples, each initially occupying a volume \(V_A+V_B\), in such a way that the final state has all of the molecules of the two gases in the same container, whose volume is also \(V_A+V_B\). While the final state of the merging process is identical to the final state of the mixing process, the initial state is distinctly different.
For ideal gases, it turns out that all of the thermodynamic functions are unchanged during the merging process. Consequently, the thermodynamic functions for mixing are just the sums of the thermodynamic functions for the reversible expansions of \(A\) and \(B\) separately. Equating thermodynamic functions for the two paths to the mixed state, we have
\[{\Delta }_{mix}E=\Delta E_A+\Delta E_B+{\Delta }_{merge}E=0 \nonumber \] \[{\Delta }_{mix}H=\Delta H_A+\Delta H_B+{\Delta }_{merge}H=0 \nonumber \]
\[{\Delta }_{mix}S=\Delta S_A+\Delta S_B+{\Delta }_{merge}S=-n_AR \ln \left(P_A/P_0\right)-n_BRT \ln \left(P_B/P_0\right) >0 \nonumber \]
\[{\Delta }_{mix}G=-T{\Delta }_{mix}S<0 \nonumber \]
The pressure ratios equal the mole fractions of the compounds in the mixture. Therefore, the entropy of mixing is also given by
\[{\Delta }_{mix}S=-n_AR{ \ln x_A\ }-n_BR{ \ln x_B\ }>0 \nonumber \]
If we calculate the entropy of mixing per mole of \(A\)–\(B\)-mixture, \({\Delta }_{mix}\overline{S}\), we find
\[{\Delta }_{mix}\overline{S}=\frac{{\Delta }_{mix}S}{n_A+n_B}=-\left(\frac{n_A}{n_A+n_B}\right)R \ln x_A-\left(\frac{n_B}{n_A+n_B}\right)R \ln x_B=-x_AR \ln x_A-x_BR \ln x_B \nonumber \]
It remains to prove our assertion that the thermodynamic functions are unchanged during the merging process. That the energy is unchanged follows from the fact that the energy of an ideal gas depends only on temperature; it is therefore independent of pressure and of the presence of any other substance. We can give a qualitative argument for the idea that other thermodynamic quantities are also unchanged. In this argument, the enthalpy, entropy, and free energy functions are unchanged because ideal gas molecules do not interact with one another. If \(A\) molecules do not interact with \(B\) molecules, it follows that the properties of the \(A\) molecules are independent of whether the \(B\) molecules share the same container or are present in a separate container of identical volume. At the same temperature, the \(A\) molecules generate a pressure \(P_A\), and the \(B\) molecules independently generate a pressure \(P_B\). Since these pressures are generated independently, we conclude that the total pressure is the sum of the two partial pressures—which is, of course, just Dalton’s law of partial pressures. The same argument applies to the enthalpy, entropy, and free energy functions, so these should also be unchanged during the merging process.
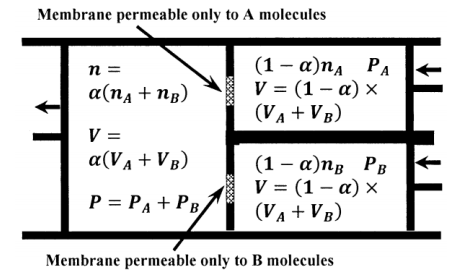
We can also create a device in which we can—in concept—carry out the reversible isothermal merging process and calculate thermodynamic-function changes. (We rely on the argument above to establish Dalton’s law of partial pressures and the conclusion that \({\Delta }_{merge}E=0\). We use the device to show from these results that there is no change in the other thermodynamic functions.) The device is sketched in Figure 2, at an intermediate stage of the process. It consists of three cylinders, each closed by a frictionless piston. The first contains unmerged gas \(A\), the second contains unmerged gas \(B\), and the third contains the mixture that results from merging them. The head of the \(A\) cylinder is shared with part of the head of the merging cylinder. Likewise, the head of the \(B\) cylinder is shared with another part of the head of the merging cylinder. We suppose that the \(A\) and \(B\) cylinder heads are comprised in part of molecule-selective gas-permeable membranes. The membrane in the head of the \(A\) cylinder allows the diffusion of \(A\) molecules in either direction, but does not permit \(B\) molecules to pass. The membrane in the head of the \(B\) cylinder allows the diffusion of \(B\) molecules in either direction, but does not permit \(A\) molecules to pass.
In the merging cylinder, we reversibly accumulate \(A\) molecules from the \(A\) cylinder and \(B\) molecules from the \(B\) cylinder. We accomplish this by controlling the pressures in the three cylinders. The pressure in the \(A\) cylinder is always infinitesimally greater than \(P_A\). The pressure in the \(B\) cylinder is always infinitesimally greater than \(P_B\). The partial pressure of \(A\) in the merging cylinder is infinitesimally less than \(P_A\); the partial pressure of \(B\) in the merging cylinder is infinitesimally less than \(P_B\); and the total pressure in the merging cylinder is infinitesimally less than \(P_A+P_B\). (There is always a difference in the total pressure across each membrane.) The system consists of the contents of the cylinders. Work is done on the system by the forces acting on the \(A\) and \(B\) cylinders. Work is done by the system on the surroundings as the merging cylinder fills with the mixture.
As far as the \(A\) cylinder is concerned, the process is reversible because the pressure due to the \(A\) molecules is just infinitesimally greater in the \(A\) cylinder than in the merging cylinder. Therefore, a very small decrease in the pressure of the \(A\) cylinder would cause the net flow of \(A\) molecules to change direction. The same is true for the \(B\) cylinder.
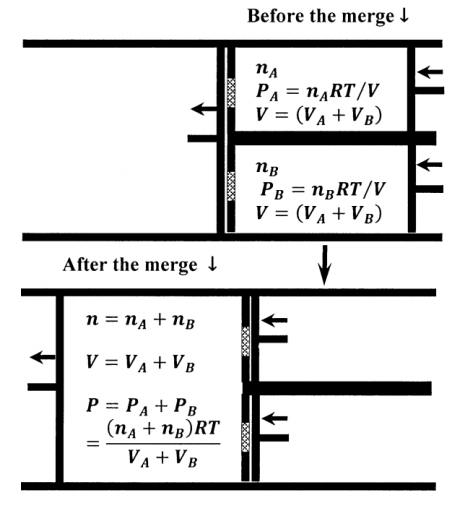
The initial and final states of the apparatus when we use it to merge \(n_A\) moles of \(A\) at \(P_A\) with \(n_B\) moles of \(B\) at \(P_A\) are shown in Figure 3. Let \(V_{mix}=V_A+V_B\) be the sum of the initial volumes of cylinders \(A\) and \(B\). This is also the final volume of the merging cylinder. The reversible work done in the \(A\) cylinder is
\[w^{rev}_A=-\int^0_{V_A+V_B}{P_AdV}=-P_A\left(0-V_A V_B\right)=P_A\left(V_A+V_B\right)=n_ART \nonumber \]
Similarly, the work in the \(B\) cylinder is
\[w^{rev}_B=P_B\left(V_A+V_B\right)=n_BRT \nonumber \]
In the merging cylinder it is
\[w^{rev}_{A+B}=-\left(P_A+P_B\right)\left(V_A+V_B\right)=-\left(n_B+n_B\right)RT \nonumber \]
For the merging process the net work is
\[w^{rev}_{merge}=w^{rev}_A+w^{rev}_B+w^{rev}_{A+B}=0 \nonumber \]
and the net change in the pressure-volume product is
\[{\Delta }_{merge}\left(PV\right)=\left(P_A+P_B\right)\left(V_A+V_B\right) \nonumber \] \[-P_A\left(V_A+V_B\right)-P_B\left(V_A+V_B\right) \nonumber \] \[=0 \nonumber \]
Since constant temperature ensures that \({\Delta }_{merge}E=0\), it follows from \({\Delta }_{merge}\left(PV\right)=0\) that \({\Delta }_{merge}H=0\), and from \(w^{rev}_{merge}=0\) that \(q^{rev}_{merge}=0\). Since the merging process is reversible, we have also that \({\Delta }_{merge}S=0\) and \({\Delta }_{merge}G=0\).
These arguments can be extended to merging any number of ideal gases. In the initial state for this merging process each gas is at the same temperature, but occupies a separate container; all of these containers have the same volume. Each gas can be at a different pressure. In the final state, all of the gases occupy a common container, whose volume is the same as the common volume of their initial containers. The temperature of the mixture in the final state is equal to the common initial temperature of the separate gases. In the final state, the partial pressure of each gas is equal to its pressure in the initial state. For any number of gases, we have
\[{\Delta }_{merge}E={\Delta }_{merge}H={\Delta }_{merge}S={\Delta }_{merge}G=0 \nonumber \]
Likewise, these arguments can be extended to the mixing of multiple ideal gases, all at the same original pressure and temperature, into a final volume that is equal to the sum of the initial volumes—and is at the original temperature. If there are \(\omega\) such gases,
\[{\Delta }_{mix}E={\Delta }_{mix}H=0 \nonumber \]
\[{\Delta }_{mix}S=\sum^{\omega }_{i=1}{-n_iR \ln x_i}>0 \nonumber \]
\[{\Delta }_{mix}G=-T{\Delta }_{mix}S<0 \nonumber \]


