10.2: dE = TdS - PdV and Internal consistency
- Page ID
- 151719
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In Chapter 1, we observe that the business of science is the creation of models that are internally consistent and that accurately describe reality. Logical deduction from tentative hypotheses is a valuable tool in our effort to create new models. Such logical arguments often take the form of “Gedanken (thought) experiments,” as exemplified by our various arguments about the properties of hypothetical, friction-free, piston engines. Nevertheless, the route by which we arrive at a theory is irrelevant; what counts are the theory’s internal consistency and predictive capability. Let us pause, therefore, to note that we have arrived at mathematical expressions of ideas that we initially introduced as principles inferred from experience.
In Chapter 6, we prove Duhem’s theorem when the variables are chosen from the set pressure, temperature, volume, and component concentrations. However, the theorem is more general. It asserts that two variables are sufficient to specify changes in the state of a closed, reversible system, in which only pressure–volume work is possible. Our derivations have now led us to the conclusion that the energy of such a system can be expressed as a function of entropy and volume. Given the entropy, the volume, and the function \(E = E\left(S,V\right)\), the relationships developed above mean that we know \(S\), \(V\), \(E\), \(P\), and \(T\) for the system. Given these, we can calculate \(H\), \(A\), and \(G\). That is, specifying the changes in the two variables \(S\) and \(V\) is sufficient to specify the change in the state of the system. Moreover, we can rearrange the fundamental equation to
\[dV = \left(\frac{T}{P}\right)dS + \left(\frac{\mathrm{1}}{P}\right)dE \nonumber \]
so that the volume can be expressed as a function of entropy and energy. Given \(S\), \(E\), and the function \(V = V\left(S,E\right)\), we can find \(P\) and \(T\). Specifying the changes in \(S\) and \(E\) is sufficient to specify the change in the system. Finally, we can rearrange the fundamental equation to
\[dS = \left(\frac{\mathrm{1}}{T}\right)dE + \left(\frac{P}{T}\right)dV \nonumber \]
so that \(S = S\left(V,E\right)\) and specifying changes in \(E\) and \(V\) is sufficient to specify the change in the system.
Now, let us return to our discussion in Section 9.7 of the entropy change for an isolated system undergoing a spontaneous change. That discussion explores the use of the machine-based statement of the second law to establish that the entropy of an isolated system must increase during any spontaneous process. To infer that the system’s entropy must increase in such a process, we consider the special case in which only pressure–volume work is possible and argue that a change in which \(\mathrm{\Delta }E = \mathrm{\Delta }S\mathrm{=0}\) is no change at all. That is, we assume that specifying the change in \(E\) and \(S\) is sufficient to specify the change in the state of such a system. It is, therefore, a significant check on the internal consistency of our thermodynamic model to see that \(dE = TdS + PdV\) implies that \(E\) and \(S\) are indeed a sufficient pair.
Finally, let us consider the relationship of a spontaneous process in a closed system to the surface that describes reversible processes in the same system. The energy of the system undergoing reversible change is expressed as \(E = E\left(S,V\right)\). An energy surface in \(V-S-E\)-space is sketched in Figure 1. At any point on this surface, the system is at equilibrium. The point \(\left(V_0,S_0,E_0\right)\) is such a point. The tangent to this surface at \(\left(V_0,S_0,E_0\right)\) and in the plane \(V = V_0\) is the partial derivative \(T = {\left({\partial E}/{\partial S}\right)}_V\). The tangent to the surface at \(\left(V_0,S_0,E_0\right)\) and in the plane \(S = S_0\) is the partial derivative \(P\mathrm{=-}{\left({\partial E}/{\partial V}\right)}_S\).
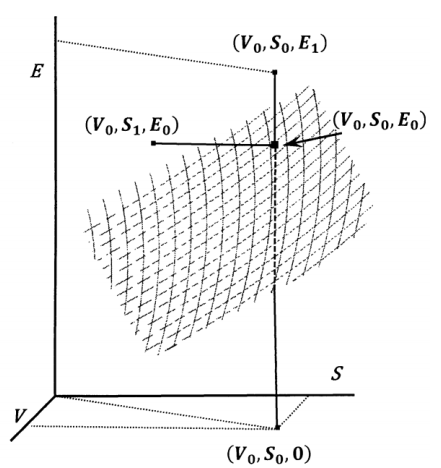
No point in \(V-S-E\)-space that is off the \(E = E\left(S,V\right)\) surface can describe an equilibrium state of the closed system. As a practical matter, some of these points may represent states that the system can attain. If so, they are transient states of a spontaneously changing system. Let us suppose, for example, that we are able to
maintain \(S = S_0\) and \(V = V_0\) while a slow chemical reaction occurs in the system. At every instant, such a state must have a non-equilibrium composition. It must have an energy, and this energy must exceed \(E_0\); since we must have \({\left(\mathrm{\Delta }E\right)}_{SV}\mathrm{<0}\) for a spontaneous process, a point \(\left(V_0,S_0,E_{\mathrm{1}}\right)\) can represent a state of the system during a spontaneous change only if \(E_{\mathrm{1}}\mathrm{>}E_0\). If \(E_{\mathrm{2}}\mathrm{<}E_0\), the point \(\left(V_0,S_0,E_{\mathrm{2}}\right)\) cannot represent a state of the system that can spontaneously go to equilibrium at \(\left(V_0,S_0,E_0\right)\). Similarly, if \(S_{\mathrm{1}}\mathrm{<}S_0\) and the system is isolated with \(E = E_0\) and \(V = V_0\), the point \(\left(V_0,S_{\mathrm{1}},E_0\right)\) represents a state of the system that can go to equilibrium at \(\left(V_0,S_0,E_0\right)\) spontaneously. This process would satisfy the entropy criterion, \({\left(\mathrm{\Delta }S\right)}_{EV}\mathrm{>0}\).


