9.26: Problems
- Page ID
- 152101
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Problems
1. Does a perpetual motion machine of the second kind violate the principle of conservation of energy?
2. What is the contrapositive of \(\left(\mathrm{SL\ and}\ \sim \mathrm{MSL}\right)\Rightarrow \left(\Delta \hat{S}<0\right)\)? It is a theorem of logic that \(\sim (\mathrm{B\ and\ C})\Rightarrow (\sim B{\mathrm{and}}/{\mathrm{or}}\sim \mathrm{C})\). Interpret this theorem. Given that SL is true and that \(\sim \left(\mathrm{SL\ and}\ \sim \mathrm{MSL}\right)\) is true, prove that \(\sim \mathrm{MSL}\) is true.
3. Max Planck introduced the following statement of the second law:
“It is impossible to construct an engine which will work in a complete cycle, and produce no effect except the raising of a weight and the cooling of a heat-reservoir.”
(M. Planck, Treatise on Thermodynamics, 3rd Edition, translated from the seventh German Edition, Dover Publications, Inc., p 89.) Since we take “raising a weight” to be equivalent to “produces work in the surroundings,” the Planck statement differs from our machine-based statement only in that it allows the temperature of the heat source to decrease as the production of work proceeds. We can now ask whether this difference has any material consequences. In particular, can we prove that the Planck statement implies our machine-based statement, or vice versa? (Suggestion: Suppose that we have identical Planck-type machines, each with its own heat reservoir. We dissipate by friction the work produced by one machine in the heat reservoir of the other.)
4. Our statements of the first and second laws have a common format: Assertion that a state function exists; operational definition by which the state function can be measured; statement of a property exhibited by this state function. Express the zero-th law of thermodynamics (Chapter 1) in this format.
5. A 0.400 mol sample of \(N_2\) is compressed from 5.00 L to 2.00 L, while the temperature is maintained constant at 350 K. Assume that \(N_2\) is an ideal gas. Calculate the change in the Helmholtz free energy, \(\Delta A\).
6. Show that \(\Delta G=\Delta A\) when an ideal gas undergoes a change at constant temperature.
7. Calculate \(\Delta E\), \(\Delta H\), and \(\Delta G\) for the process in problem 5.
8. A sample of 0.200 mol of an ideal gas, initially at 5.00 bar, expands reversibly and isothermally from 1.00 L to 10.00 L. Calculate \(\Delta E\), \(\Delta H\), and \(\Delta G\) for this process.
9. A 100.0 g sample of carbon tetrachloride is compressed from 1.00 bar to 10.00 bar at a constant temperature of 20 C. At 20 C, carbon tetrachloride is a liquid whose density is \(1.5940\ \mathrm{g}\ \mathrm{m}{\mathrm{L}}^{-1}\). Assume that the density does not change significantly with pressure. What is \(\Delta G\) for this process?
10. Calculate the Helmholtz free energy change (\(\Delta A\)) in problem 9.
11. If \(C_V\) is constant, show that the initial and final temperatures and volumes for an adiabatic ideal-gas expansion are related by the equation \[\left(\frac{T_f}{T_i}\right)=\left(\frac{V_i}{V_f}\right)^{R/C_V} \nonumber \]
12. At 25 C, the initial volume of a monatomic ideal gas is 5 L at 10 bar. This gas expands to 20 L against a constant applied pressure of 1 bar.
(a) Is this process impossible, spontaneous, or reversible?
(b) What is the final temperature?
(c) Find \(q\), \(w\), \(\Delta E\), and \(\Delta H\) for this process.
13. The same change of state experience by the monatomic ideal gas in problem 12 can be effected in two steps. Let step A be the reversible cooling of the gas to its final temperature while the pressure is maintained constant at 10 bar. Let step B be the reversible isothermal expansion of the resulting gas to a pressure of 1 bar.
(a) Find \(q\), \(w\), \(\Delta E\), and \(\Delta H\) for step A.
(b) Find \(q\), \(w\), \(\Delta E\), and \(\Delta H\) for step B.
(c) From your results in (a) and (b), find\(\ q\), \(w\), \(\Delta E\), and \(\Delta H\) for the overall process of step A followed by step B.
(d) Compare the values of \(q\), \(w\), \(\Delta E\), and \(\Delta H\) that you find in (c) to the values for the same overall process that you found in problem 12.
(e) Find \(\Delta S\) and \(\Delta \hat{S}\) for step A.
(f) Find \(\Delta S\) and \(\Delta \hat{S}\) for step B.
(g) Find \(\Delta S\), \(\Delta \hat{S}\), and \(\Delta S_{universe}\) for the overall process.
14. Assume that the process in problem 12 occurs while the gas is in thermal contact with its surroundings and that the temperature of the surroundings is always equal to the final temperature of the gas. Find \(\Delta \hat{S}\) and \(\Delta S_{universe}\) for this process.
15. At 25 C, the initial volume of a monatomic ideal gas is 5 L at 10 bar. The gas expands to 20 L while in thermal contact with surroundings at 125 C. During the expansion, the applied pressure is constant and equal to the equilibrium pressure at the final volume and temperature.
(a) Is this process impossible, spontaneous, or reversible?
(b) Find \(q\), \(w\), \(\Delta E\), \(\Delta H\), and \(\Delta \hat{S}\) for this process.
(c) Find \(\Delta S\) and \(\Delta S_{universe}\) for this process. To find \(\Delta S\), it is necessary to find a reversible alternative path that effects the same change in the system’s state functions.
16. At 60 C, the density of water is \(\mathrm{0.98320\ g}\ {\mathrm{cm}}^{-3}\), the vapor pressure is 19,932 Pa, and the enthalpy of vaporization is \(42,482\mathrm{\ J}\ {\mathrm{mol}}^{-1}\). Assume that gaseous water behaves as an ideal gas. A vessel containing liquid and gaseous water is placed in a constant 60 C bath, and the applied pressure is maintained at 19,932 Pa while 100 g of water vaporizes.
(a) Is this process impossible, spontaneous, or reversible?
(b) Find \(q\), \(w\), \(\Delta E\), \(\Delta H\), \(\Delta S\), \(\Delta A\), and \(\Delta G\) for this process.
(c) Is \({\left(\Delta S\right)}_{EV}=0\) a criterion for equilibrium that applies to this system? Why or why not? \({\left(\Delta H\right)}_{SP}=0\)? \({\left(\Delta A\right)}_{VT}=0\)? \({\left(\Delta G\right)}_{PT}=0\)?
17. This problem compares the efficiency and \(\sum{q/T}\) for one mole of a monatomic ideal gas taken around a reversible Carnot cycle to the same quantities for the same gas taken around an irreversible cycle using the same two heat reservoirs.
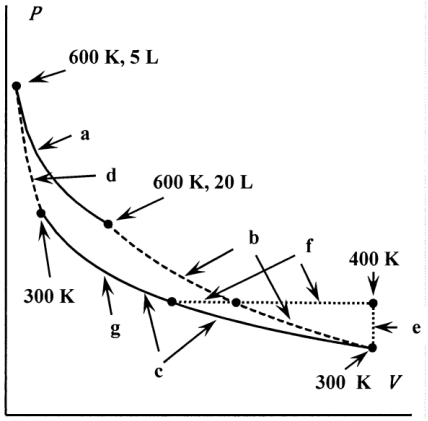
(i) Let the successive step of the reversible Carnot cycle be a, b, c, and d. Isothermal step a begins with the gas occupying 5.00 L at 600 K and ends with the gas occupying 20.00 L. Adiabatic expansion step b ends with the gas at 300 K. After the isothermal compression step c, the gas is adiabatically compressed in step d to the original state. Find \(P\), \(V\), and \(T\) for the gas at the end of each step of this reversible cycle. Find \(\sum q/\hat{T}\), \(\Delta S\), and \(\Delta \hat{S}\) for the cycle a, b, c, d. What is the efficiency of this cycle?
(ii) Suppose that following step b, the ideal gas is warmed at constant volume to 400 K by exchanging heat with the 600 K reservoir. Call this step e. Following step e, the gas is cooled at constant pressure to 300 K by contact with the 300 K reservoir. Call this step f. Following step f, the gas is isothermally and reversibly compressed at 300 K to the same \(P\), \(V\), and \(T\) as the gas reaches at the end of step c. Call this step g. Find \(P\), \(V\), and \(T\) for the gas at the ends of steps e, f, and g. Although steps e and f are not reversible, the same changes can be effected reversibly by keeping \(T=\hat{T}\) as the gas is warmed at constant volume (step e) and cooled at constant pressure (step f). (We discuss this point in further in Section 12.4.) Consequently, \({\Delta }_eS=\int^{400\ K}_{300\ K} \frac{C_V}{T}dT\) and \({\Delta }_fS=\int^{400\ K}_{300\ K} \frac{C_P}{T}dT\). Find \(\sum q/\hat{T}\), \(\Delta S\), and \(\Delta \hat{S}\), and \(\Delta S_{universe}\) for the cycle a, b, e, f, g, d. What is the efficiency of this cycle?
(iii) Compare the value of \(\sum q/ \hat{T}\) that you obtained in part (ii) to value of \(\sum q/ \hat{T}\) that you obtained in part (i).
(iv) Clausius’ theorem states that \(\sum q/ \hat{T}=0\) for a cycle traversed reversibly, and \(\sum q/ \hat{T}<0\) for a cycle traversed spontaneously. Comment.
18. For a spontaneous cycle traversed while the temperature changes continuously, Clausius’ theorem asserts that \(\oint{dq/\hat{T}}<0\). Show that this inequality follows from the result, \(dS>dq/ \hat{T}\), that we obtained in Section 9.15 for any spontaneous process in a closed system.
19. In Sections 9.6 through 9.8, we conclude that \(\Delta S+\Delta \hat{S}=0\) is necessary for a reversible process, \(\Delta S+\Delta \hat{S}>0\) is necessary for a spontaneous process, and \(\Delta S+\Delta \hat{S}<0\) is necessary for an impossible process. That is: \[(\mathrm{Process\ is\ reversible})\ \ \ \Rightarrow \ \left(\Delta S+\Delta \hat{S}=0\right) \nonumber \] (\(\mathrm{Process\ is\ spontaneous}\))\(\ \ \Rightarrow \left(\Delta S+\Delta \hat{S}>0\right)\), and (\(\mathrm{Process\ is\ impossible}\)) \(\ \ \Rightarrow \left(\Delta S+\Delta \hat{S}<0\right)\).
Since we have defined the categories reversible, spontaneous, and impossible so that they are exhaustive and mutually exclusive, the following proposition is true:
\[\sim \left(\mathrm{Process\ is\ spontaneous}\right)\ \mathrm{and}\ \sim \left(\mathrm{Process\ is\ impossible}\right) \nonumber \] \[\Rightarrow \left(\mathrm{Process\ is\ reversible}\right) \nonumber \]
(a) Prove that \(\Delta S+\Delta \hat{S}=0\) is sufficient for the process to be reversible; that is, prove: \[\left(\Delta S+\Delta \hat{S}=0\right)\ \ \Rightarrow \ \ \left(\mathrm{Process\ is\ reversible}\right) \nonumber \]
(b) Prove that \(\Delta S+\Delta \hat{S}>0\) is sufficient for the process to be spontaneous; that is, prove: \[\left(\Delta S+\Delta \hat{S}>0\ \right)\ \Rightarrow \ \ \left(\mathrm{Process\ is\ spontaneous}\right) \nonumber \]
(c) Prove that \(\Delta S+\Delta \hat{S}<0\) is sufficient for the process to be impossible; that is, prove: \[\left(\Delta S+\Delta \hat{S}<0\right)\ \ \Rightarrow \ \ \left(\mathrm{Process\ is\ impossible}\right) \nonumber \]
20. Label the successive steps in a reversible Carnot cycle A, B, C, and D, where A is the point at which the pressure is greatest.
(a) Sketch the path ABCD in \(P\)–\(V\) space.
(b) Sketch the path ABCD in \(T\)–\(dq^{rev}/T\) space.
(c) Sketch the path ABCE in \(T\)– \(q^{rev}\) space.
(d) Sketch the path BCDA in \(T\)– \(q^{rev}\) space.
(e) Sketch the path CDAB in \(T\)– \(q^{rev}\) space.
(d) Sketch the path DABC in \(T\)– \(q^{rev}\) space.
21. Assume that the earth’s atmosphere is pure nitrogen and that it behaves as an ideal gas. Assume that the molar energy of this nitrogen is constant and that its molar entropy changes are adequately modeled by \(d\overline{S}=\left({C_V}/{T}\right)dT+\left({R}/{\overline{V}}\right)d\overline{V}\). For this atmosphere, show that \[{\left(\frac{\partial T}{\partial h}\right)}_E=\frac{-\overline{M}g}{C_V} \nonumber \] where \(h\) is the height above the earth’s surface, \(\overline{M}\) is the molar mass of dinitrogen (\(0.0280\ \ \mathrm{kg}\ {\mathrm{mol}}^{-1}\)), \(g\) is the acceleration due to gravity (\(\mathrm{9.80}\ \mathrm{m}\ {\mathrm{s}}^{-1}\)), and \(C_V\) is the constant-volume heat capacity (\(20.8\ \mathrm{J}\ {\mathrm{K}}^{-1}\ {\mathrm{mol}}^{-1}\)). [Suggestion: Write the total differential for \(\overline{E}=\overline{E}\left(\overline{S},\overline{V},h\right)\). What are \({\left({\partial \overline{E}}/{\partial \overline{S}}\right)}_{\overline{V},h}\), \({\left({\partial \overline{E}}/{\partial \overline{V}}\right)}_{\overline{S},h}\), and \({\left({\partial \overline{E}}/{\partial h}\right)}_{\overline{S},\overline{V}}\)?]
If the temperature at sea level is 300 K, what is the temperature on the top of a 3000 m mountain?
22. Assume that the earth’s atmosphere is pure nitrogen and that it behaves as an ideal gas. Assume that the molar enthalpy of this nitrogen is constant and that its molar entropy changes are adequately modeled by \(d\overline{S}=\left({C_P}/{T}\right)dT-\left({R}/{P}\right)dP\). For this atmosphere, show that \[{\left(\frac{\partial T}{\partial h}\right)}_S=\frac{-\overline{M}g}{C_P} \nonumber \] where \(h\) is the height above the earth’s surface, \(\overline{M}\) is the molar mass of dinitrogen (\(0.0280\ \ \mathrm{kg}\ {\mathrm{mol}}^{-1}\)), \(g\) is the acceleration due to gravity (\(\mathrm{9.80}\ \mathrm{m}\ {\mathrm{s}}^{-1}\)), and \(C_P\) is the constant-pressure heat capacity (\(29.1\ \mathrm{J}\ {\mathrm{K}}^{-1}\ {\mathrm{mol}}^{-1}\)). [Suggestion: Write the total differential for\(\ \overline{H}=\overline{H}\left(\overline{S},P,h\right)\). What are \({\left({\partial \overline{H}}/{\partial \overline{S}}\right)}_{P,h}\), \({\left({\partial \overline{H}}/{\partial P}\right)}_{\overline{V},h}\), and \({\left({\partial \overline{H}}/{\partial h}\right)}_{\overline{S},\overline{V}}\)?]
Use this approximation to calculate the temperature on the top of a 3000 m mountain when the temperature at sea level is 300 K.
23. Hikers often say that, as a rule-of-thumb, the temperature on a mountain decreases by 1 C for every 100 m increase in elevation. Is this rule in accord with the relationships developed in problems 21 and 22? In these problems, we assume that the temperature of an ideal-gas atmosphere varies with altitude but that the molar energy or enthalpy does not. Does this assumption contradict the principle that the energy and enthalpy of an ideal gas depend only on temperature?
24. Derive the barometric formula (Section 2.10) from the assumptions that the earth’s atmosphere is an ideal gas whose molar mass is \(\overline{\boldsymbol{M}}\) and whose temperature and Gibbs free energy are independent of altitude.
25. Run in reverse, a Carnot engine consumes work \(\left(w>0\right)\) and transfers heat \(\left(q_{\ell }>0\right)\) from a low-temperature reservoir to a high temperature reservoir \(\left(q_h<0\right)\). The work done by the machine is converted to heat that is discharged to the high-temperature reservoir. In one cycle of the machine, \(\Delta E=q_{\ell }+q_h=0\). For a refrigerator—or for a heat pump operating in air-conditioning mode—we are interested in the quantity of heat removed \(\left(q_{\ell }\right)\) per unit of energy expended \(\left(w\right)\). We define the coefficient of performance as \(COP\left(cooling\right)={q_{\ell }}/{w}\). This is at a maximum for the reversible Carnot engine. Show that the theoretical maximum is \[COP\left(cooling\right)=\frac{1-\epsilon }{\epsilon }=\frac{T_{\ell }}{T_h-T_{\ell }} \nonumber \] where \(\epsilon\) is the reversible Carnot-engine efficiency, \[\epsilon =1-\frac{T_{\ell }}{T_h} \nonumber \] 26. For a heat pump operating in heating mode—as a “furnace”—we are interested in the quantity of heat delivered to the space being heated \(\left(-q_h\right)\) per unit of energy expended \(\left(w\right)\). We define the coefficient of performance as \(COP\left(heating\right)=-{q_h}/{w}\). Show that the theoretical maximum is \[COP\left(heating\right)=\frac{1}{\epsilon }=\frac{T_h}{T_h-T_{\ell }} \nonumber \]
27. For \(T_{\ell }=300\ \mathrm{K}\) and \(T_h=500\ \mathrm{K}\), calculate the theoretical maxima for \(COP\left(cooling\right)\) and \(COP\left(heating\right)\).
28. Find the theoretical maximum \(COP\left(cooling\right)\) for a refrigerator at \(40\ \mathrm{F}\) in a room at \(72\ \mathrm{F}\).
29. Find the theoretical maximum \(COP\left(cooling\right)\) for a heat pump that keeps a room at \(72\ \mathrm{F}\) when the outside temperature is \(100\ \mathrm{F}\).
30. Find the theoretical maximum \(COP\left(heating\right)\) for a heat pump that keeps a room at \(72\ \mathrm{F}\) when the outside temperature is \(32\ \mathrm{F}\).
Notes
\({}^{1}\) For an introduction to the concept of internal entropy and its applications, see Ilya Prigogine, Introduction to the Thermodynamics of Irreversible Processes, Interscience Publishers, 1961.


