9.15: Entropy and Spontaneous Change
- Page ID
- 152090
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In a reversible process, the changes that occur in the system are imposed by the surroundings; reversible change occurs only because the system responds to changes in the conditions imposed on it by its surroundings. A reversible process is driven by the surroundings. In contrast, a spontaneous process is driven by the system. Nevertheless, when a spontaneous process occurs under some specific set of imposed conditions (specific values of the temperature and pressure, for example) the system’s equilibrium state depends on these conditions. To specify a particular spontaneous change, we must specify enough constraints to fix the final state of the system.
To see these points from a slightly different perspective, let us consider a closed reversible system in which only pressure–volume work is possible. Duhem’s theorem asserts that a change in the state of this system can be specified by specifying the changes in some pair of state functions, say \(X\) and \(Y\). If the imposed values of \(X\) and \(Y\) are constant at their eventual equilibrium values, but the system is changing, the system cannot be on a Gibbsian equilibrium manifold. We say that the system is undergoing a spontaneous change at constant\(\ X\) and \(Y\).
This description is a figure of speech in that the system’s \(X\) and \(Y\) values do not necessarily attain the imposed values and become constant until equilibrium is reached. An example is in order: A system whose original pressure and temperature are \(P_i\) and \(T_i\) can undergo a spontaneous change while the surroundings impose a constant pressure, \(P_{applied}=P_f\), and the system is immersed in constant temperature bath at \(T=T_f\). The pressure and temperature of the system may be indeterminate as the process occurs, but the equilibrium pressure and temperature must be \(P_f\) and \(T_f\).
If the surroundings operate to impose particular values of \(\boldsymbol{X}\) and \(\boldsymbol{Y}\) on the system, then the position at which the system eventually reaches equilibrium is determined by these values. The same equilibrium state is reached for any choice of surroundings that imposes the same values of \(\boldsymbol{X}\) and \(\boldsymbol{Y}\) on the system at the time that the system reaches equilibrium. For every additional form of non-pressure–volume work that affects the system, we must specify the value of one additional variable in order to specify a unique equilibrium state.
The entropy changes that occur in the system and its surroundings during a spontaneous process have predictive value. However, our definitions do not enable us to find the entropy change for a spontaneous process, and the temperature of the system may not have a meaningful value. On the other hand, we can always carry out the process so that the temperature of the surroundings is known at every point in the process. Indeed, if the system is in thermal contact with its surroundings as the process occurs, we cannot specify the conditions under which the process occurs without specifying the temperature of the surroundings along this path.
Figure 9 describes a spontaneous process whose path can be specified by the values of thermodynamic variable \(Y\) and the temperature of the surroundings, \(\hat{T}\), as a function of time, \(t\). Let us denote the curve that describes this path as \(C\). We can divide this path into short intervals. Let \(C_k\) denote a short segment of this path along which the temperature of the surroundings is approximately constant. For our present purposes, the temperature of the system, \(T\), is irrelevant; since the process is spontaneous, the temperature of the system may have no meaningful value within the interval \(C_k\). As the system traverses segment \(C_k\), it accepts a quantity of heat, \(q_k\), from the surroundings, which are at temperature \({\hat{T}}_k\). The heat exchanged by the surroundings within \(C_k\) is \({\hat{q}}_k=-q_k\). Below, we show that it is always possible to carry out the process in such a way that the change in the surroundings occurs reversibly. Then
\[\Delta {\hat{S}}_k=\frac{{\hat{q}}_k}{{\hat{T}}_k}=-\frac{q_k}{{\hat{T}}_k} \nonumber \]
and since \(\Delta S_k+\Delta {\hat{S}}_k>0\), it follows that
\[\Delta S_k>\frac{q_k}{{\hat{T}}_k} \nonumber \]
This is the Clausius inequality. It plays a central role in the thermodynamics of spontaneous processes. When we make the intervals \(C_k\) arbitrarily short, we have
\[dS_k>\frac{{dq}_k}{{\hat{T}}_k} \nonumber \]
To demonstrate that we can measure the entropy change in the surroundings during a spontaneous process, let us use a conceptual device to transfer the heat, \(q_k\), that must be exchanged from the surroundings at temperature, \(\hat{T}_k\) to the system. As sketched in Figure 10, we imagine a very small, reversible, ideal-gas Carnot engine, whose high-temperature reservoir is also very small. We suppose that the Carnot engine delivers a very small heat increment \(\delta q\) to the high temperature reservoir in every cycle. While the system is within \(C_k\), we maintain the Carnot engine’s high temperature reservoir at \(\hat{T}_k\), and allow heat \(q_k\) to pass from the high temperature reservoir to the system. The high temperature reservoir is the only part of the surroundings that is in thermal contact with the system; \(q_k\) is the only heat exchanged by the system while it is within \(C_k\).
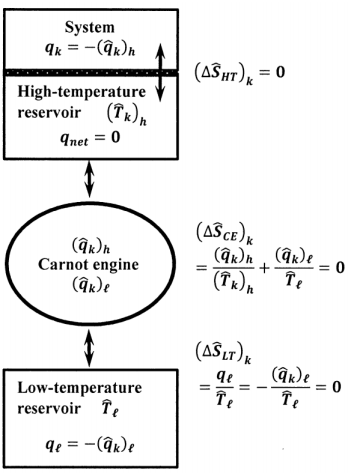
To maintain the high temperature reservoir at \({\hat{T}}_k\) we operate the Carnot engine for a large integral number of cycles, \(n\), such that \(q_k\approx n\times \delta q\), and do so at a rate that just matches the rate at which heat passes from the high-temperature reservoir to the system. When the system passes from path-segment \(C_k\) to path-segment \(C_{k+1}\), we alter the steps in the reversible Carnot cycle to maintain the high-temperature reservoir at the new surroundings temperature, \({\hat{T}}_{k+1}\). The low-temperature heat reservoir for this Carnot engine is always at the constant temperature \({\hat{T}}_{\ell }\). Let the heat delivered from the high-temperature reservoir to the Carnot engine within \(C_k\) be \({\left({\hat{q}}_k\right)}_h\). We have \(q_k=-{\left({\hat{q}}_k\right)}_h\). Let the heat delivered from the low-temperature reservoir to the Carnot engine within \(C_k\) be \({\left({\hat{q}}_k\right)}_{\ell }\). Let the heat delivered to the low-temperature reservoir within \(C_k\) be \(q_{\ell }\). We have \(q_{\ell }=-{\left({\hat{q}}_k\right)}_{\ell }\). Since the Carnot engine is reversible, we have
\[\frac{\left(\hat{q}_k\right)_h}{\hat{T}_k}+\frac{\left( \hat{q}_k\right)_{\ell }}{\hat{T}_{\ell }}=0 \nonumber \]
and
\[-\frac{q_k}{\hat{T}_k}-\frac{q_{\ell }}{\hat{T}_{\ell }}=0 \nonumber \]
so that
\[\frac{q_{\ell }}{\hat{T}_{\ell }}=-\frac{q_k}{\hat{T}_k} \nonumber \]
While the system is within \(C_k\), it receives an increment of heat \(q_k\) from the high temperature reservoir. Simultaneously, three components in the surroundings also exchange heat. Let the entropy changes in the high-temperature reservoir, the Carnot engine, and the low-temperature reservoir be \({\left(\Delta {\hat{S}}_{HT}\right)}_k\), \({\left(\Delta {\hat{S}}_{CE}\right)}_k\), and \({\left(\Delta {\hat{S}}_{LT}\right)}_k\), respectively. The high temperature reservoir receives heat \(q_k\) from the Carnot engine and delivers the same quantity of heat to the system. The net heat accepted by the high temperature reservoir is zero. No change occurs in the high-temperature reservoir. We have \({\left(\Delta {\hat{S}}_{HT}\right)}_k=0\). The reversible Carnot engine completes an integral number of cycles, so that \({\left(\Delta {\hat{S}}_{CE}\right)}_k=0\). The low temperature reservoir accepts heat \({-\left({\hat{q}}_k\right)}_{\ell }=q_{\ell }\), at the fixed temperature \({\hat{T}}_{\ell }\), during the reversible operation of the Carnot engine, so that
\[\left(\Delta \hat{S}_{LT}\right)_k=\frac{q_{\ell }}{\hat{T}_{\ell }}=-\frac{q_k}{\hat{T}_k} \nonumber \]
The entropy change in the surroundings as the system passes through \(C_k\) is
\[\Delta \hat{S}_{k}= \left(\Delta \hat{S}_{HT}\right)_k+ \left(\Delta \hat{S}_{CE}\right)_k+\left(\Delta \hat{S}_{LT}\right)_k=\frac{q_{\ell }}{\hat{T}_{\ell }}=-\frac{q_k}{\hat{T}_k} \nonumber \]
so that, as we observed above,
\[\Delta S_k >- \Delta {\hat{S}}_k =\frac{q_k}{\mathrm{\ }{\hat{T}}_k} \nonumber \]
Since \(C_k\) can be any part of path C, and \(C_k\) can be made arbitrarily short, we have for every increment of any spontaneous process occurring in a closed system that can exchange heat with its surroundings, \(d\hat{S}=-{dq}/{\hat{T}}\), and
\[dS>\frac{dq}{\hat{T}} \nonumber \]
If the temperature of the surroundings is constant between any two points A and B on curve C, we can integrate over this interval to obtain \(\mathrm{\Delta }_{\mathrm{AB}}\widehat{\mathrm{S}}\mathrm{=-} \mathrm{q}_{\mathrm{AB}}/\widehat{\mathrm{T}}\) and
\[\mathrm{\Delta }_{\mathrm{AB}}\mathrm{S>}\frac{\mathrm{q}_{\mathrm{AB}}}{\widehat{\mathrm{T}}} \nonumber \]
For an adiabatic process, \(q=0\). For any arbitrarily small increment of an adiabatic process, \(dq=0\). It follows that \(\Delta S>0\) and \(dS>0\) for any spontaneous adiabatic process.


