5.19: Microscopic Reversibility and the Second Law
- Page ID
- 152020
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The principle of microscopic reversibility requires that parallel mechanisms give rise to the same expression for the concentration-dependence of the equilibrium constant. That is, the function that characterizes the equilibrium composition must be the same for each mechanism. If, for the reaction \(aA+bB\rightleftharpoons cC+dD\), the equilibrium composition for mechanism \(1\) is \({\left[A\right]}_1\),\(\ {\left[B\right]}_1\),\(\ {\left[C\right]}_1\),\(\ {\left[D\right]}_1\), and that for mechanism \(2\) is \({\left[A\right]}_2\),\(\ {\left[B\right]}_2\),\(\ {\left[C\right]}_2\),\(\ {\left[D\right]}_2\), microscopic reversibility asserts that
\[K_1=\frac{{\left[C\right]}^c_1{\left[D\right]}^d_1}{{\left[A\right]}^a_1{\left[B\right]}^b_1} \nonumber \]
and
\[K_2=\frac{{\left[C\right]}^c_2{\left[D\right]}^d_2}{{\left[A\right]}^a_2{\left[B\right]}^b_2} \nonumber \]
In and of itself, microscopic reversibility makes no assertion about the value of \({\left[A\right]}_1\) compared to that of \({\left[A\right]}_2\). While microscopic reversibility asserts that the same function characterizes the concentration relationships for parallel mechanisms, it does not assert that the numerical value of this function is necessarily the same for each of the mechanisms.
However, that these numerical values must be equal follows directly when we introduce another of our most basic observations. No matter how many mechanisms may be available to a reaction in a particular system, the concentration of any reagent can have only one value in an equilibrium state. At equilibrium, \({\left[A\right]}_1={\left[A\right]}_2\), etc.; therefore, the numerical values of the equilibrium constants must be the same: \(K_1=K_2\).
The uniqueness of the equilibrium composition is a fundamental feature of our ideas about what chemical equilibrium means. Nevertheless, it is of interest to show that we can arrive at this conclusion from a different perspective: We can use an idealized machine to show that the second law of thermodynamics requires that parallel mechanisms must produce the same the equilibrium composition. Our argument is a proof by contradiction.
Let us suppose that \(A\), \(B\), and \(C\) are gases. Suppose that the reaction \(A\to B+C\) occurs in the absence of a catalyst, but that reaction occurs in the opposite direction, \(C+B\to A\), when a catalyst is present. More precisely, we assume that the position of equilibrium \(A\rightleftharpoons B+C\) lies to the right in the absence of the catalyst and to the left in its presence, while all other reaction conditions are maintained constant. These assumptions mean that the equilibrium composition for the catalyzed mechanism is different from that of the mechanism that does not involve the catalyst.
We can show that these assumptions imply that the second law of thermodynamics is false. If we accept the validity of the second law, this violation means that the assumptions cannot in fact describe any real system. (We are getting a bit ahead of ourselves here, inasmuch as our detailed consideration of the laws of thermodynamics begins in Chapter 6.)
Given our assumptions, we can build a machine consisting of a large cylinder, closed by a frictionless piston. The cylinder contains a mixture of \(A\), \(B\), and \(C\), and a quantity of the catalyst. We provide a container for the catalyst, and construct the device so that the catalyst container can be opened and closed from outside the cylinder. Finally, we immerse the entire cylinder in a fluid, which we maintain at a constant temperature.
When the catalyst container is sealed, so that the gaseous contents of the cylinder are not in contact with the catalyst, reaction occurs according to \(A\to B+C\), and the piston moves outward, doing work on the surroundings. When the catalyst container is open, reaction occurs according to \(C+B\to A\), and the piston moves inward. Figure \(\PageIndex{1}\) shows these changes schematically. At the end of a cycle, the machine is in exactly the same state as it was in the beginning, and the temperature of the reaction mixture is the same at the end of a cycle as it was at the beginning. By connecting the piston to a load, we can do net work on the load as the machine goes through a cycle. For example, if we connect the piston to a mechanical device that converts the reciprocating motion of the piston into rotary motion, we can wind a rope around an axle and thereby lift an attached weight.
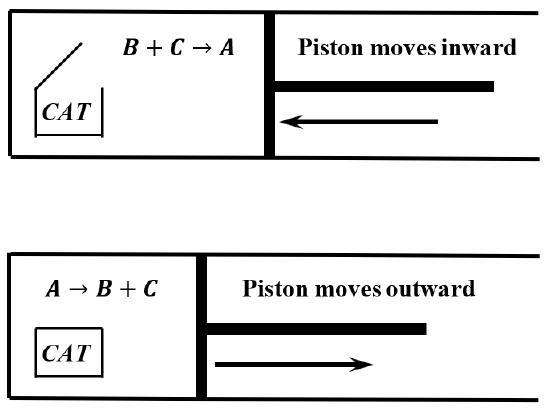
We can operate this machine as an engine by alternately opening and closing the catalyst container. We can make the cylinder as large as we want, so the energy we expend in opening and closing the catalyst container can be made arbitrarily small compared to the amount of work we get out of the machine in a given cycle. All of this occurs with the machine maintained at a constant temperature. If energy is conserved, the machine must absorb heat from the bath during the cycle; otherwise, the machine would be doing work with no offsetting consumption of energy. This would be a violation of the first law of thermodynamics. (See Sections 5.7-5.11.)
From experience, we know that this machine cannot function in the manner we have described. This experience is embodied in the second law of thermodynamics we know that it is impossible to construct a machine that operates in a cycle, exchanges heat with its surroundings at only one temperature, and produces work in the surroundings (Section 9-1). Our argument assumes that two reaction mechanisms are available in a particular physical system, that they consume the same reactants, that they produce the same products, and that the equilibrium compositions are different. These assumptions imply that the second law is false. Since we are confident that it is possible for some system to satisfy the first three of these assumptions, the second law requires that the last one be false: the equilibrium compositions must be the same.
We see that there is a complementary relationship between microscopic reversibility and this statement of the second law. Microscopic reversibility asserts that a unique function of concentrations characterizes the equilibrium state for any reaction mechanism, but does not require that every mechanism reach the same state at equilibrium. This statement of the second law implies that a reaction’s equilibrium composition unique, but it does not specify a law relating the equilibrium concentrations of the reacting species. (In Chapters 9 and 13, we see that, by augmenting this statement of the second law with some additional ideas, we are led to a more rigorous statement, from which we are eventually able to infer the same functional form for the equilibrium constant.)
Microscopic reversibility asserts that a unique function of concentrations characterizes the equilibrium state for any reaction mechanism, but does not require that every mechanism reach the same state at equilibrium.
G. N. Lewis gave an early statement of the principle of microscopic reversibility. He called it “the law of entire equilibrium,” and observed that it is “a law which in its general form is not deducible from thermodynamics, but proves to be compatible with the laws of thermodynamics in all cases where a comparison is possible.”
It is worth noting that we have not shown that the existence of a unique equilibrium state implies either microscopic reversibility or the second law. Also, even though the principle of microscopic reversibility is inferred from the laws of mechanics, our development of the equilibrium constant relationship—which we do view as a law of thermodynamics—depends on our equations for the rates of elementary reactions. Our rate equations are not logical consequences of the laws of motion. Rather, they follow from assumptions we make about the average behavior of systems that contain many molecules. Consequently, we should not suppose that we have deduced a thermodynamic result (the condition for chemical equilibrium) solely from the laws of mechanics. In Section 12-2, we give brief additional consideration to the relationship between the theories of mechanics and thermodynamics. Beginning in Chapter 20, we develop thermodynamic equations by applying statistical models to the distribution of molecular energy levels.


