1.8: Particulate Metals
- Page ID
- 25361
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)As mentioned in the Introduction, macroscopic single crystals of metals are not generally employed in technological applications.
Massive metallic structures (electrodes etc.) are polycrystalline in nature - the size of individual crystallites being determined by the mechanical treatment and thermal history of the metal concerned. Nevertheless, the nature and properties of the exposed polycrystalline, metal surface is still principally determined by the characteristics of the individual crystal surfaces present. Furthermore, the proportions in which the different crystal surfaces occur is controlled by their relative thermodynamic stabilities. Thus, a macroscopic piece of an fcc metal will generally expose predominantly (111)-type surface planes.
A more interesting case for consideration is that of metals in a highly dispersed system - the classic example of which is a supported metal catalyst (such as those employed in the petrochemical industries and automotive catalytic converters). In such catalysts the average metal particle size is invariably sub-micron and may be as small as 1 nm . These metal particles are often tiny single crystals or simple twinned crystals.
The shape of these small crystals is principally determined by the surface free energy contribution to the total energy. There are two ways in which the surface energy can be reduced for a crystal of fixed mass / volume:
- By minimizing the surface area of the crystallite
- By ensuring that only surfaces of low surface free energy are exposed.
If matter is regarded as continuous then the optimum shape for minimizing the surface free energy is a sphere (since this has the lowest surface area/volume ratio of any 3D object) - this is why liquid droplets in free space are basically spherical.
Unfortunately, we cannot ignore the discrete, atomic nature of matter and the detailed atomic structure of surfaces when considering particles of the size found in catalysts. If, for example, we consider an fcc metal (eg. Pt) and ensure that only the most stable (111)-type surfaces are exposed, then we end up with a crystal which is an octahedron.
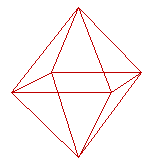
Octahedron exposing. 8 symmetry-related. fcc(111)-type faces
There are 8 different, but crystallographically-equivalent, surface planes which have the (111) surface structure - the {111} faces. They are related by the symmetry elements of the cubic fcc system.
A compromise between exposing only the lowest energy surface planes and minimizing the surface area is obtained by truncating the vertices of the octahedron - this generates a cubo-octahedral particle as shown below, with 8 (111)-type surfaces and 6 smaller, (100)-type surfaces and gives a lower (surface area / volume) ratio.
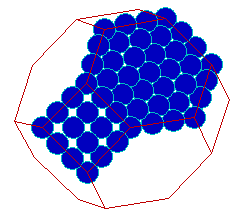
Crystals of this general form are often used as conceptual models for the metal particles in supported catalysts.
The atoms in the middle of the {111} faces show the expected CN=9 characteristic of the (111) surface. Similarly, those atoms in the centre of the {100} surfaces have the characteristic CN=8 of the (100) surface. However, there are also many atoms at the corners and intersection of surface planes on the particle which show lower coordination numbers.
What is the lowest coordination number exhibited by a surface atom on this crystallite ?
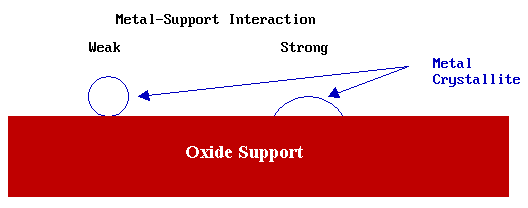
This model for the structure of catalytic metal crystallites is not always appropriate: it is only reasonable to use it when there is a relatively weak interaction between the metal and the support phase (e.g. many silica supported catalysts).
A stronger metal-support interaction is likely to lead to increased "wetting" of the support by the metal, giving rise to:
- a greater metal-support contact area
- a significantly different metal particle morphology
In the case of a strong metal-support interaction the metal/oxide interfacial free energy is low and it is inappropriate to consider the surface free energy of the metal crystallite in isolation from that of the support.
Our knowledge of the structure of very small particles comes largely from high resolution electron microscopy (HREM) studies - with the best modern microscopes it is possible to directly observe such particles and resolve atomic structure.


