1.7: Relaxation and Reconstruction
- Page ID
- 25360
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The phenomena of relaxation and reconstruction involve rearrangements of surface ( and near surface ) atoms, this process being driven by the energetics of the system i.e. the desire to reduce the surface free energy (see Energetics of Surfaces). As with all processes, there may be kinetic limitations which prevent or hinder these rearrangements at low temperatures. Both processes may occur with clean surfaces in ultrahigh vacuum, but it must be remembered that adsorption of species onto the surface may enhance, alter or even reverse the process !
I. Relaxation
Relaxation is a small and subtle rearrangement of the surface layers which may nevertheless be significant energetically, and seems to be commonplace for metal surfaces. It involves adjustments in the layer spacings perpendicular to the surface, there is no change either in the periodicity parallel to the surface or to the symmetry of the surface.
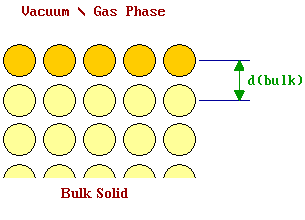
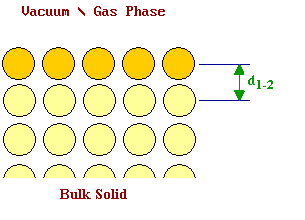
Figure (left) Unrelaxed Surface and (right) Relaxed Surface with \(d_{1-2} < d_{bulk}\).
The right picture shows the relaxed surface: the first layer of atoms is typically drawn in slightly towards the second layer (i.e. d1-2 < dbulk ). We can consider what might be the driving force for this process at the atomic level. If we use a localized model for the bonding in the solid then it is clear that an atom in the bulk is acted upon by a balanced, symmetrical set of forces.
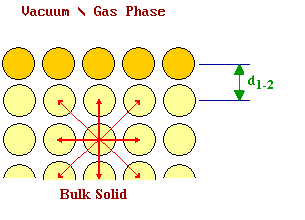
On the other hand, an atom at the unrelaxed surface suffers from an imbalance of forces and the surface layer of atoms may therefore be pulled in towards the second layer.
(Whether this is a reasonable model for bonding in a metal is open to question !)
The magnitude of the contraction in the first layer spacing is generally small ( < 10 % )- compensating adjustments to other layer spacings may extend several layers into the solid.
II. Reconstruction
The reconstruction of surfaces is a much more readily observable effect, involving larger (yet still atomic scale) displacements of the surface atoms. It occurs with many of the less stable metal surfaces (e.g. it is frequently observed on fcc(110) surfaces), but is much more prevalent on semiconductor surfaces.
Unlike relaxation, the phenomenon of reconstruction involves a change in the periodicity of the surface structure - the diagram below shows a surface, viewed from the side, which corresponds to an unreconstructed termination of the bulk structure.
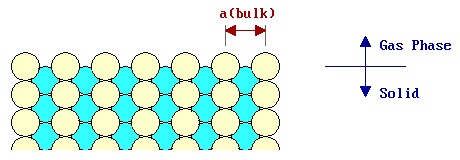
This may be contrasted with the following picture which shows a schematic of a reconstructed surface - this particular example is similar to the "missing row model" proposed for the structure of a number of reconstructed (110) fcc metal surfaces.
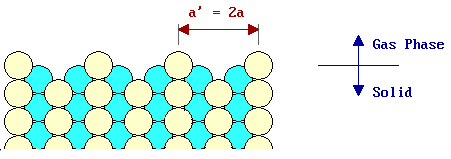
Since reconstruction involves a change in the periodicity of the surface and in some cases also a change in surface symmetry, it is readily detected using surface diffraction techniques (e.g. LEED & RHEED ).
The overall driving force for reconstruction is once again the minimization of the surface free energy - at the atomic level, however, it is not always clear why the reconstruction should reduce the surface free energy. For some metallic surfaces, it may be that the change in periodicity of the surface induces a splitting in surface-localized bands of energy levels and that this can lead to a lowering of the total electronic energy when the band is initially only partly full.
In the case of many semiconductors, the simple reconstructions can often be explained in terms of a "surface healing" process in which the co-ordinative unsaturation of the surface atoms is reduced by bond formation between adjacent atoms. For example, the formation of a Si(100) surface requires that the bonds between the Si atoms that form the new surface layer and those that were in the layer immediately above in the solid are broken - this leaves two "dangling bonds" per surface Si atom.
A relatively small co-ordinated movement of the atoms in the topmost layer can reduce this unsatisfied co-ordination - pairs of Si atoms come together to form surface "Si dimers", leaving only one dangling bond per Si atom. This process leads to a change in the surface periodicity: the period of the surface structure is doubled in one direction giving rise to the so-called (2x1) reconstruction observed on all clean Si(100) surfaces [ Si(100)-(2x1) ].
|
More examples: |
|
|
Si(111)-(7x7) |
From the web-pages of the Omicron NanoTechnology GmbH (showing data courtesy of Prof. Hongiun Gao´s group, Institute of Physics, CAS, Beijing, China). |
In this section, attention has been concentrated on the reconstruction of clean surfaces. It is, however, worth noting that reconstruction of the substrate surface is frequently induced by the adsorption of molecular or atomic species onto the surface - this phenomenon is known as adsorbate-induced reconstruction (see Section 2.5 for some examples).
Summary
The minimization of surface energy means that even single crystal surfaces will not exhibit the ideal geometry of atoms to be expected by truncating the bulk structure of the solid parallel to a particular plane. The differences between the real structure of the clean surface and the ideal structure may be imperceptibly small (e.g. a very slight surface relaxation ) or much more marked and involving a change in the surface periodicity in one or more of the main symmetry directions ( surface reconstruction ).


