Ideal Gas Processes
- Page ID
- 1915
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In this section we will talk about the relationship between ideal gases in relations to thermodynamics. We will see how by using thermodynamics we will get a better understanding of ideal gases.
Introduction
In the realm of Chemistry we often see many relations between the former and its relations to Physics. By utilizing both Chemistry and Physics we can get a better understanding for the both mentioned. We will use what we know about Ideal Gases and Thermodynamics to try to understand specific processes that occur in a system.
A Quick Recap on Thermodynamics
Before we discuss any further, let’s do a very quick recap on the important aspects of thermodynamics that are important to know for ideal gas processes. Some of this will be a quick review and some will be relatively new unless you have seen it in your Physics class.
So first off let’s state the First law of thermodynamics:
\(\Delta{U} = Q + W\)
The whole point of stating this equation is to remind us that energy within any given system is conserved. What that means is that no energy is EVER created or destroyed, but it is simply converted from one form to another, such as heat to work and vice versa.
In case you may be confused with some of these symbols, here is a short explanation in a table.
| ΔU | This is the total change in the internal energy of the gas. |
| Q | This is the total heat flow of the gas • When Q is negative (-), heat is being removed from the system • When Q is positive (+), heat is being added to the system |
| W | This is the total work done on or by the gas • When W is negative (-), work is being done by the system • When W is positive (+), work is being done on system |
Thermodynamic and Ideal Gases
Below are two equations that describe the relationship between the internal energy of the system of a monatomic gas and a diatomic gas. In a monatomic (mono-: one) gas, since it only has one molecule, the ways for it have energy will be less than a diatomic gas (di-: two) since a diatomic gas has more ways to have energy (Hence, diatomic gas has a 5/2 factor while a monatomic gas has a 3/2).
Looking at these two equations we have also conclude that the internal energy (ΔU) only has an effect on the kinetic energy of the gas molecules (movement). Nowhere in these two equations do we see that the potential energy being affected.
A Monatomic Ideal Gas
A Monatomic Ideal Gas Equation:
\(\Delta{U} = \frac{3}{2}nR\Delta{T}\)
In a monatomic gas, it has a total of three translational kinetic energy modes (hence, the 3/2).
A Diatomic Ideal Gas
A Diatomic Ideal Gas Equation:
\(\Delta{U} = \frac{5}{2}nR\Delta{T}\)
In a diatomic gas, it has a total of three translational kinetic energy modes and two rotational energy modes (hence, the 5/2).
Work in Ideal Gases
In relations to the first law of thermodynamics, we can see that by adding heat (Q) or work (W) the internal energy of the gaseous system can be increased. Also, that during compression of the system, the volume of the gas will decrease and response its temperature will increase and thus the internal energy of the system will also increase since temperature is related to energy. And this is true except in an isothermal system (which we’ll talk more about later). That is why when a gas is compressed the work is positive and when it is being compressed, it is negative.

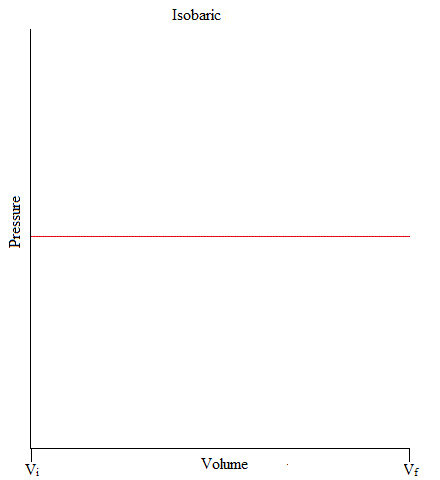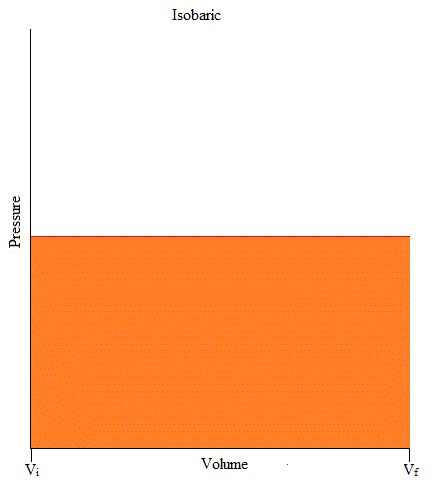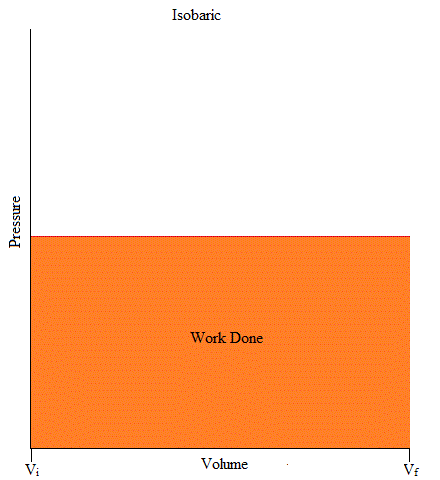
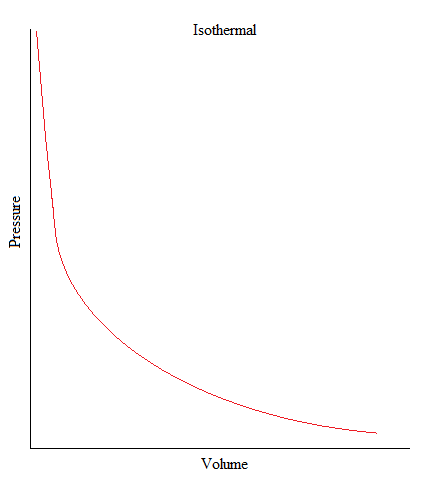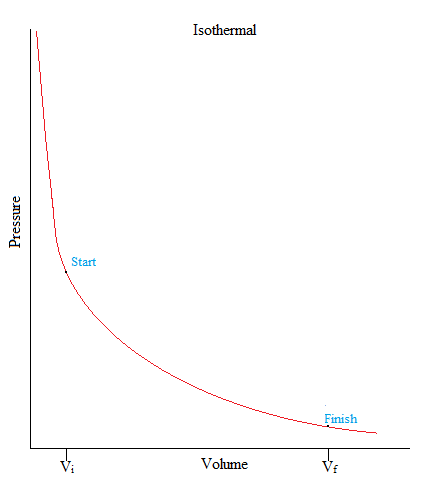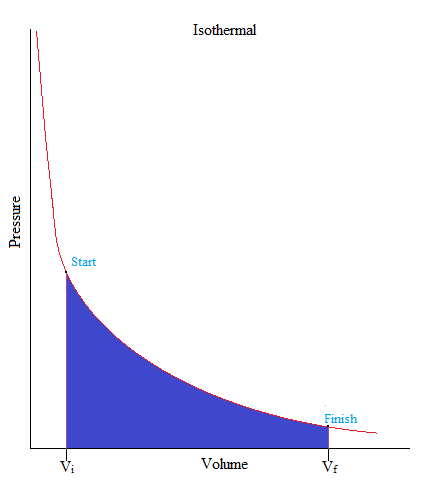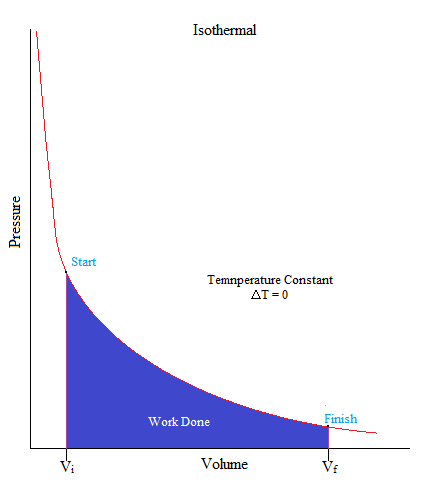
It may also be good to know that the area under the curve is work. If you have taken Calculus, you may remember the integral as it is used to find the area under the curve (or graph) as shown below.
\[W = -\displaystyle \int P dV\]
OR
W = - (area under curve)
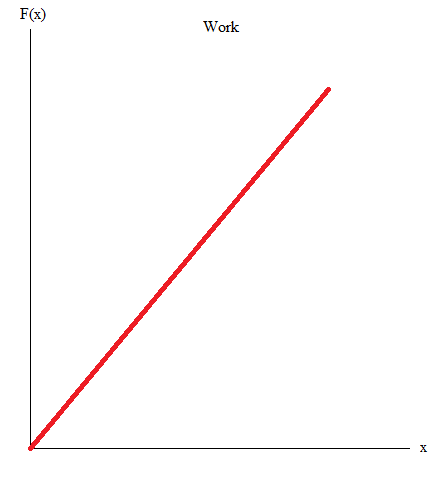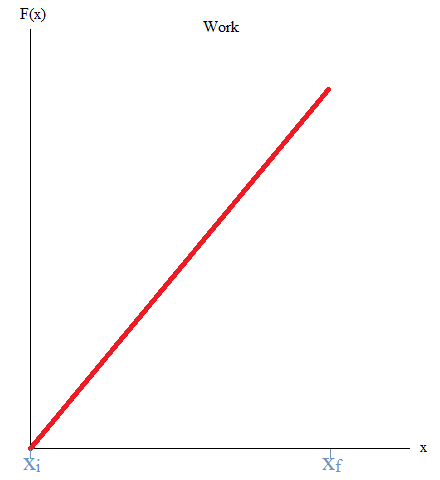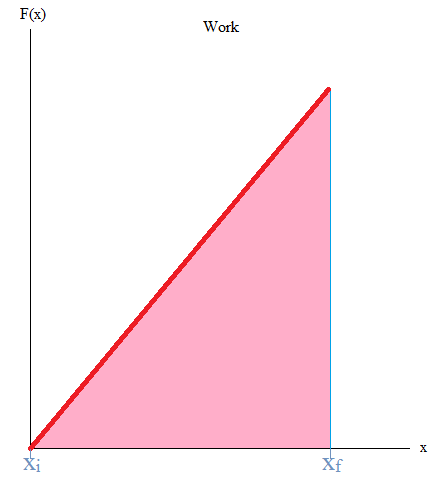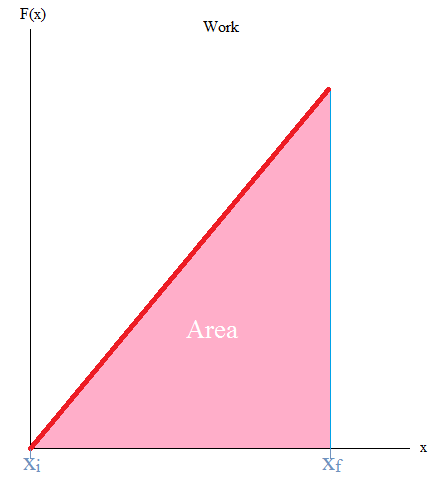
In this case, you can literally take the area of the triangle or work with integrals.
Work = Area = (1/2)base x height
or
Work = ∫F(x) dx
The Heat Capacity and State Functions
When certain state functions (P, V, T) are held constant, the specific heat of the gas is affected. Below is the universal formula for a gas molecule when its pressure is held constant:
\( c_p = c_v + R\)
When this formula is rearranged we get the heat capacity of the gas when its volume is held constant:
\( c_v = R - c_p\)
Types of Ideal Gas Processes
There are four types of thermodynamics processes. What this basically means is that in a system, one or more variable is held constant. To keep things simple, below are examples as to how keeping a certain variable in a system constant can lead to.
Isobaric
This is a process where the pressure of the system is kept constant.
\[\Delta P = 0 \nonumber\]
An example of this would be when water is boiling in a pot over a burner. In this case, heat is being exchanged between the burner and pot but the pressure stays constant.

To derive this process we start off by using what we know, and that is the first law of thermodynamics:
\(\Delta{U} = Q + W\)
Rearranging this equation a bit we get:
\( Q = \Delta{U} + W\)
Next, since pressure is equal to \(W ΔV\), it can be denoted as:
\(Q = \Delta{U} + p\Delta{V}\)
Now, the ideal gas law can be applied (PV=nRΔT) and since pressure is constant:
\(Q = ΔU + nR\Delta{T}\)
For the next step, we will assume that this number of moles of gas stays constant throughout this process:
\(Q = n \ c_V\ \Delta{T} + nR\Delta{T}\)
Simplifying the equation some more by taking out the nΔT from both equations we get:
\(Q = n (c_V + R)\ \Delta{T}\)
Knowing that cp = cv + R we can substitute for cp:
\(Q = n \ c_P\ \Delta{T} \)
Now we got the equation for an isobaric process!
Isochoric
This is a process where the volume of the system is kept constant.
\[ΔV = 0 \nonumber\]
An example of this would be when you have Helium gas sealed up in a container and there is an object (like a piston) pushing down the container (exerting pressure). But, gas molecules is neither entering nor exiting out of the system.
Let’s find the equation for this process, as before let’s start off with the first law of thermodynamics:
\(\Delta{U} = Q + W\)
Rearranging this equation a bit we get:
\( Q = \Delta{U} + W\)
In this case, since volume is constant, ΔV = 0:
\(Q = \Delta{U}\)
Since the internal energy of the system equals to the amount of heat transferred we can replace ΔU with the ideal gas equation for heat:
\(Q = nC_V\Delta{T}\)
Above is the ideal gas equation for an isochoric process!
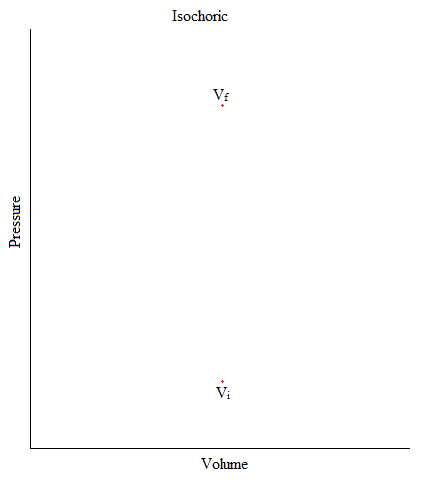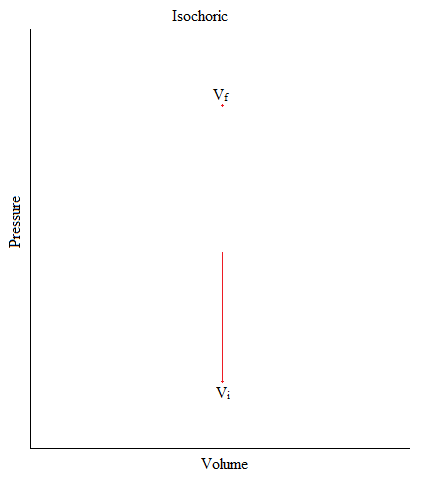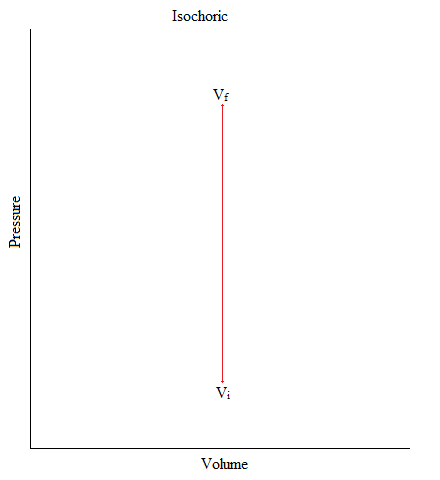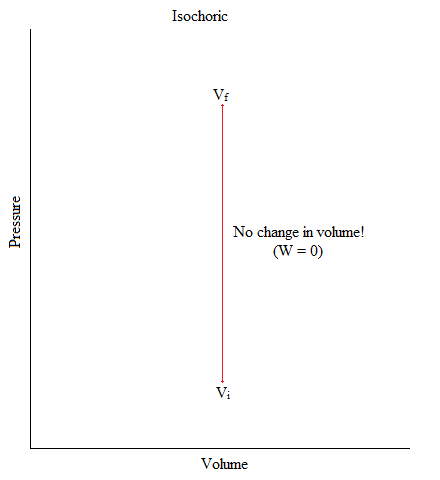
Figure: Isochoric Process in Graphical Form
Isothermal
•This is a process where the temperature of the system is kept constant.
ΔU = 0, ΔT = 0
•When volume increases, the pressure will decrease, and vice versa.
ΔT = 0 then:ΔV ↑and P ↓ OR ΔV↓ and P ↑ (inverse relationship)
•As an example, gas molecules are sealed up in a container but an object on top of the container (such as a piston) pushes down on the container in a very slow fashion that there is not enough to change its temperature.
To derive the equation for an isothermal process we must first write out the first law of thermodynamics:
\(\Delta{U} = Q + W\)
Rearranging this equation a bit we get:
\( Q = \Delta{U} + W\)
Since ΔT = 0. Therefore we are only left with work:
\( Q = W \)
As such we get:
\( W = -p\Delta{V} \)
Making this equation into an ideal gas equation we get:
\( W = \frac{nRt}{V} \)
In order to get to the next step we need to use some calculus:
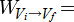
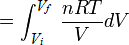
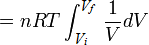
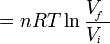
\(Q = nRT ln \frac{V_f}{V_i} \)
And there you go! The equation for an isothermal process.
Adiabatic
•This is a process where no heat is being added or removed from the system.
•Or can be simply stated as: no heat transfer (or heat flow) happening in a system.
•In freshman chemistry, only the basic idea of this process is needed and that is when there is no heat transfer, Q = 0.
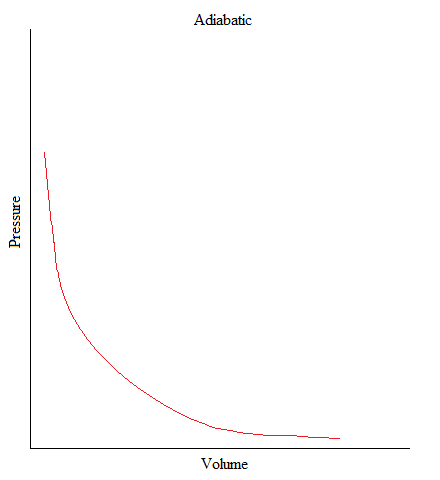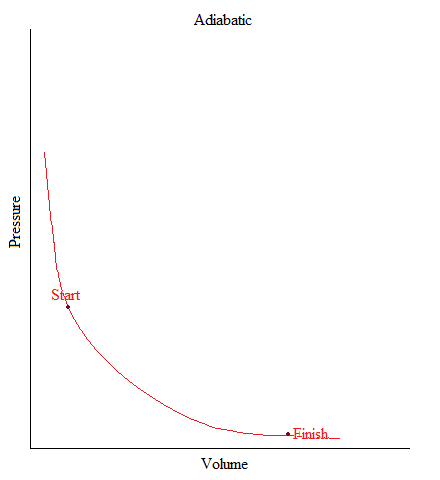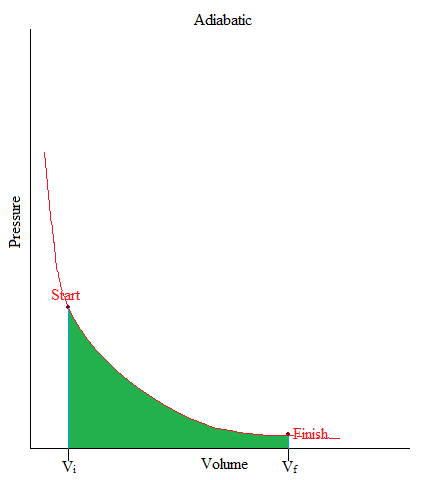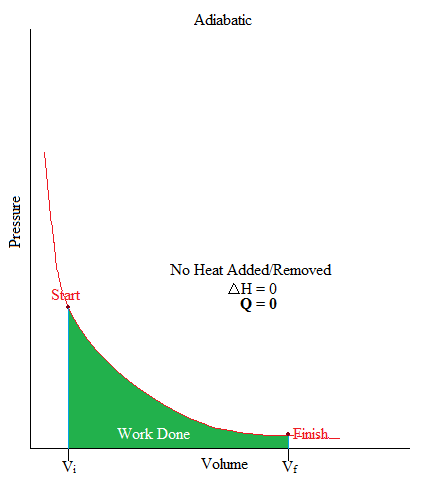
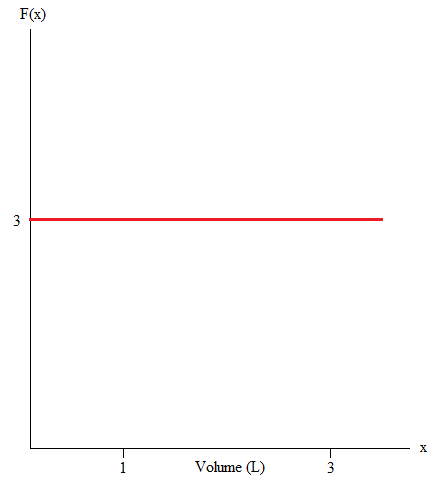
The volume of a gas in a container expanded from 1L to 3L upon releasing the piston upward. From following graph, find the amount work associated with the expansion of the gas.
\(f(x) = x + 3\) from [1, 3]
Solution
As stated above, we know that the amount of work is the same as saying the area under the curve. In this case we can look for shapes we can easily find the area of.
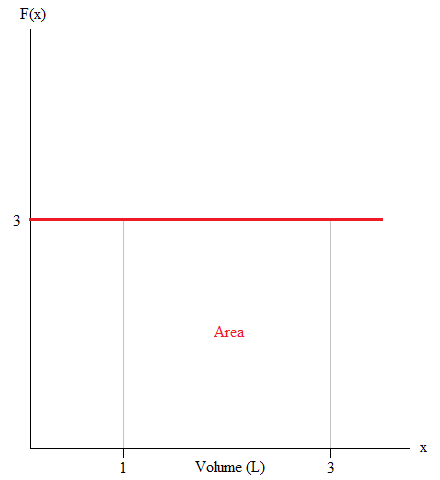
Here, we have a shape that is similar to a rectangle.
Work= Area = Length x Width
= (3)(3-1)
=(3)(2)
=6
Work = 6 Joules
Calvin is observing an unknown monatomic gas molecule (sealed inside a container) in his Freshman Chemistry Lab. He has been told by his lab instructor that there are four moles of this unidentified gas in the container. The laboratory room’s temperature was initially set at room temperature when he started the lab, but by the time he was almost finished with the lab the temperature has gone up 10°C. What is the total internal energy of this unknown gaseous substance by the time Calvin’s lab session ended?
Solution
From the problem, we know that the unknown gaseous substance is monatomic, so we would have to use the equation for a monatomic gas:
\(\Delta{U} = \frac{3}{2}nR\Delta{T}\)
Also from the problem, we know that the substance is at room temperature with is 25°C, but that was just extra information given and we didn’t really need to know that to solve the problem. Since we know that the temperature change from start to finish was +10°.
\(\Delta{T} = +10K\)
The problem also given us the number of moles that was in the container:
\(n = 4 mol\)
For the R-value, we can choose any R constant, but to make this problem a little easier we will choose a R-constant that will cancel out any other units except for joules.
\(R = 8.3145 \frac{J}{mol K}\)
Plugging in all these values into the equation we have:
\(\Delta{U} = \frac{3}{2}(4 mol)(8.3145 \frac{J}{mol K})(10K)\)
\(= 498 J\)
In an isochoric system, three moles of hydrogen gas is trapped inside an enclosed container with a piston on top of it. The total amount of internal energy of the gaseous system is 65 Joules, and the temperature of the system decreased from 25°C to 19°C. What is the specific heat of the gas molecules?
Solution
Since the system is an isochoric system, there will be zero change in volume, therefore:
\(\Delta{V} = 0\)
And the equation for an isochoric system will be:
\(Q = nC_V\Delta{T}\)
From the equation we know the following:
\( n=3mol\)
\(Q = \Delta{T}=(25-19)K=6K\)
(Since we are only trying to find the difference between the starting point and the final point, we do not need to do conversions to degrees Kelvin)
\( Q=65J\)
Before plugging the values in, let’s rearrange the isochoric equation and set it to what we are trying to find:
\( C_V = \frac{Q}{n\Delta{T}}\)
Now, we can plug the values in:
\( C_V = \frac{65J}{(3mol)(6K)}\)
\( = 3.6\frac{J}{mol k}\)
While looking over some of her lab data, a chemistry student notices she forgot to record the numbers of moles of the gas molecule she looked at. The experiment she did that day had kept the pressure constant and the temperature went down two degrees in the process of the experiment. Assuming all variables are also ideal, how many moles was she dealing with?
Solution
From the problem we are given the following:
\( \Delta{T} = +2K\)
\( \Delta{U} = Q = 110 J\)
Since are given that the pressure of the gas was kept constant:
\( C_p = 14\frac{J}{K mol}\)
We have enough evidence to conclude that this is an isobaric process:
\(Q = n\c_P\ \Delta{T} \)
Rearranging the equation to fit what we are trying to find we get:
\(n = \frac{Q}{\c_P\ \Delta{T}} \)
Now we can plug in our values:
\(n = \frac{110 J}{14\frac{J}{K mol}2K} \)
\(= 4 moles of gas\)
A chemistry student is looking at 5.00 grams of the monatomic Helium gas that is put into a container that expands from 10 L to 13 L. The container is confined at a constant temperature of 30°C in an enclosed system.
- What is the total energy of the system?
- Is the pressure of the system increasing, decreasing, or not affected?
Solution A
First, let’s list what is given in the problem:
\( V_i = 10 L\)
\( V_f = 13 L\)
Converting temperature from Celsius to Kelvin we have:
\(T = (30+273.15)K = 303.15K\)
And since temperature is constant, this is an isothermal process:
\(Q = nRT ln \frac{V_f}{V_i} \)
In order to use this equation we will need to convert Helium gas to moles:
\(n = \frac{grams}{\frac{grams}{mole}}\)
\( = \frac{5.00 g He}{\frac{4.00 g He}{mol He}}\)
\( = 1.25 mol He\)
We will choose a universal R-constant that will easily cancel out all the units that will help us get the answer without any other conversions:
\( = 8.31451\frac{J}{K mol}\)
Plugging in all these values into the isothermal equation we get:
\(Q = (1.25 mol)(8.31451 \frac{J}{K mol})(303.15 K) ln \frac{13 L}{10 L} \)
\( = 827 J\)
Solution B
It is a rule that in an isothermal process that volume and pressure have an inverse relationship. Meaning in one goes up, the other must go down. In this case, volume went up so the pressure must have decreased.
References
- Waite, Boyd A. "A Gas Kinetic Explanation of Simple Thermodynamic Processes." Journal of Chemical Education 62.3 (1985): 224-27. Print.
- Gislason, Eric A., and Norman C. Craig. "General Definitions of Work and Heat in Thermodynamic Processes." Journal of Chemical Education 64.8 (1987): 660-68. Print.
- Snider, Eric H. Ideal Gas Law, Enthalpy, Heat Capacity, Heats of Solution and Mixing. New York: American Institute of Chemical Engineers, 1984. Print.
- Redfern, Francis. "Physics Book - Chapter 13." Texarkana College. 2001. Web. 28 Feb. 2011. <prism.tc.cc.tx.us/physicsbook/cha13.html>.
- Young, Hugh D., Roger A. Freedman, Francis Weston Sears, and Hugh D. Young. Sears and Zemansky's University Physics. San Francisco: Pearson/Addison Wesley, 2004. 748-51. Print.


