Differential Scanning Calorimetry
- Page ID
- 1898
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Calorimetry involves the experimental quantification of heat released in a chemical process, either a reaction or a conformational alteration. It can be used to determine parameters such as the Heat of Reaction (\(Δ_{r}H\)), which is the change in enthalpy associated with the process of a chemical reaction. When \(Δ_{r}H\) is a negative value, the process is exothermic and releases heat; when \(Δ_{r}H\) is a positive value, the process is endothermic and requires heat input. Calorimetry uses a closed system, meaning there is a system separated from its surroundings by some boundary, through which heat and energy but not mass are able to flow. Calorimetry may be conducted at either constant pressure or volume and allows one to monitor the change in temperature as a result of the chemical process being investigated.
Introduction
Differential scanning calorimetry is a specific type of calorimetry including both a sample substance and a reference substance, residing in separate chambers. While the reference chamber contains only a solvent (such as water), the sample chamber contains an equal amount of the same solvent in addition to the substance of interest, of which the ΔrH is being determined. The \(Δ_{r}H\) due to the solvent is constant in both chambers, so any difference between the two can be attributed to the presence of the substance of interest. Each chamber is heated by a separate source in a way that their temperatures are always equal. This is accomplished through the use of thermocouples; the temperature of each chamber is constantly monitored and if a temperature difference is detected, then heat will be added to the cooler chamber to compensate for the difference. The heating rate used to maintain equivalent temperatures is logged as a function with respect to the temperature.
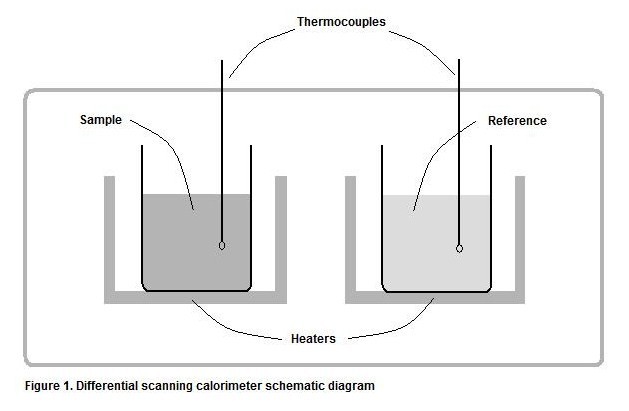
For example, if the experimental goal is to determine the \(Δ_{r}H\) of a protein denaturation process, the reference cell could contain 100 mL H2O, and the sample cell could contain 1 mg of the protein in addition to the same 100 mL H2O. Therefore, the contribution of the solvent (H2O) to the heat capacity of each cell would be equal, and the only difference would be the presence of the protein in the sample chamber.
Equations
The following equation relates the change in temperature to the change in enthalpy:
\[ dH = \int^{T_f}_{T_i}nC_p dt \]
where \(dH\) is the rate of change in enthalpy, \(C_P\) is the molar heat capacity of the calorimeter, \(dT\) is the rate of change in temperature, \(n\) is the number of moles of material, and \(T_i\) and \(T_f\) are the initial and final temperatures, respectively. This equation can be integrated to yield
\[\Delta H = nC_p \Delta T\]
where ΔH is the total change in enthalpy and ΔT is the change in temperature.
Differential Thermograms
The output yielded by differential scanning calorimetry is called a differential thermogram, which plots the required heat flow against temperature. Data analysis is highly dependent on the assumption that both the reference and sample cells are constantly and accurately maintained at equal temperatures.
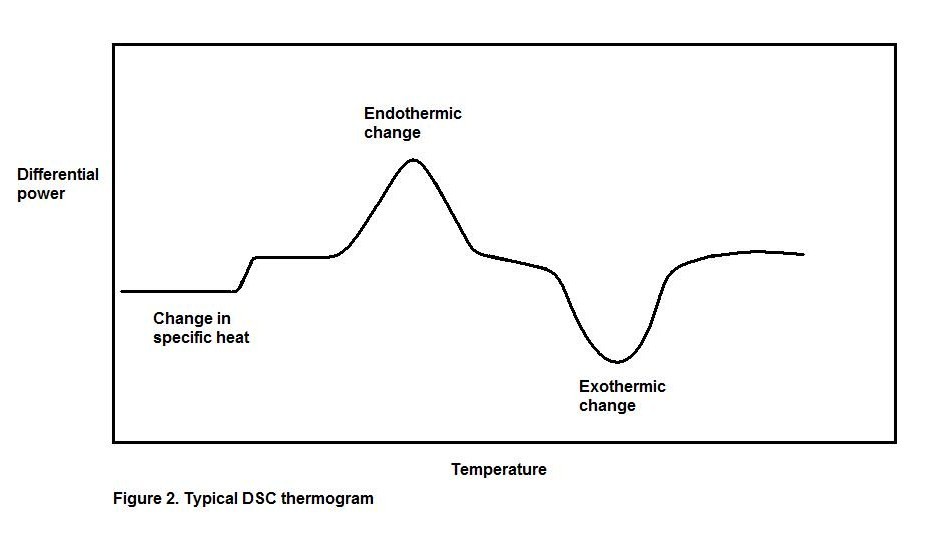
This graph indicates the change in power (electrical heat) as the temperatures of the two cells are gradually increased. A change in specific heat results in a small change in power, and can be either positive or negative depending on the particular process. The advent of an endothermic reaction will cause an increase in power as temperature increases, since additional heat is required to drive the reaction and still maintain the reference temperature. When an exothermic reaction occurs, the opposite effect is observed; power decreases because heat is released by the reaction and less power is required to maintain equivalent temperatures in the chambers.
Examples
Differential scanning calorimetry can be used to study many different fields including biopolymer energetics where it is used to find the enthalpy of the protein denaturation process. A protein can be changed from its native state, in which it has a specific conformation due to non-covalent intramolecular interactions, to a denatured state where this characteristic structure is altered. Analysis of proteins through DSC can provide both the enthalpy of denaturation and information about the cooperativity of the denaturation process. A sharper peak in the thermogram indicates a higher level of cooperativity, meaning that when one structural association is disturbed, the likelihood of disruption at other points of association will be enhanced.
DSC is also used in conjunction with differential thermal analysis. Through the combination of these two techniques, thermal behavior of inorganic compounds can be studied while the melting, boiling and decomposition points of organic compounds and polymers are found.
References
- Skoog, Douglas A. Principles of Instrumental Analysis. Brooks/Cole, 1985. Print.
- Chang, Raymond. Physical Chemistry for the Biosciences. New York: University Science, 2005. Print.
Contributors and Attributions
- Alyssa Cassabaum and Valerie Winton (HOPE)

