11. The Microcanonical Ensemble
- Page ID
- 9160
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The goal of equilibrium statistical mechanics is to calculate the diagonal elements of \(\rho_{e q}\) so we can evaluate average observables \(\langle A\rangle=\operatorname{Tr}\left\{A \rho_{e q}\right\}=A\) that give us fundamental relations or equations of state.
Just as thermodynamics has its potentials \(\mathrm{U}, \mathrm{A}, \mathrm{H}, \mathrm{G}\) etc., so statistical mechanics has its ensembles, which are useful depending on what macroscopic variables are specified. We first consider the microcanonical ensemble because it is the one directly defined in postulate II of statistical mechanics.
In the microcanonical ensemble \(U\) is fixed (Postulate I), and other constraints that are fixed are the volume \(V\) and mole number \(n\) (for a simple system), or other extensive parameters (for more complicated systems).
Definition of the partition function
The 'partition function' of an ensemble describes how probability is partitioned among the available microstates compatible with the constraints imposed on the ensemble.
In the case of the microcanonical ensemble, the partitioning is equal in all microstates at the same energy: according to postulate II, with \(p_{i}=\rho_{i i}^{(e q)}=1 / W(U)\) for each microstate "i" at energy U. Using just this, we can evaluate equations of state and fundamental relations.
2. Calculation of thermodynamic quantities from W(U)
Example 1: Fundamental relation for lattice gas: entropy-volume part.
Consider again the model system of a box with \(\mathrm{M}=\mathrm{V} / \mathrm{V}_{0}\) volume elements \(\mathrm{V}_{0}\) and \(\mathrm{N}\) particles of volume \(\mathrm{V}_{0}\), so each particle can fill one volume elements. The particles can randomly hop among unoccupied volume elements to randomly sample the full volume of the box. This is a simple model of an ideal gas. As shown in the last chapter,
\[W=\dfrac{M !}{(M-N) ! N !}\]
for identical particles, and we can approximate this, if \(\mathrm{M}<<\mathrm{N}\) by
\[W \approx \dfrac{1}{N !}\left(\dfrac{V}{V_{0}}\right)^{N}\]
since \(M ! /(M-N !) \approx M^{N}\) in that case. Assuming the hopping samples all microstates so the system reaches equilibrium, we compute the equilibrium entropy, as proved in chapter 10 from postulate III, as
\[S=k_{B} \ln W \approx S_{0}+N k_{B} \ln \left(V / V_{0}\right)\]
where \(S_{0}\) is independent of volume. This gives the volume dependence of the entropy of an ideal gas. Note that by taking the derivative \((\partial \mathrm{S} / \partial \mathrm{V})=k_{B} \mathrm{~N} / \mathrm{V}=\mathrm{P} / \mathrm{T}\) we can immediately derive the ideal gas law \(\mathrm{PV}=\mathrm{N} k_{B} \mathrm{~T}=\mathrm{nRT}\).
Example 2: Fundamental relation for a lattice gas: entropy-energy part.
The above model does not give us the energy dependence, since we did not explicitly consider the energy of the particles, other than to assume there was enough energy for them to randomly hop around. We now remedy this by considering the energy levels of particles in a box. The result will also demonstrate once more that \(\tilde{\Omega}\) increases so ferociously fast that it is equal to \(\mathrm{W}\) with incredibly high accuracy for more than a handful of particles.
Let the total energy \(U\) be randomly distributed among particles in a box of volume \(L^{3}=\) \(\mathrm{V}\). The energy is given by
\[U=\dfrac{1}{2 m} \sum_{i=1}^{3 N} p_{i}^{2},\]
where \(\mathrm{i}=1,2,3\) are the \(\mathrm{x}, \mathrm{y}, \mathrm{z}\) coordinates of particle #1, and so forth to \(\mathrm{i}=3 N-2,3 N-1,3 N\) are the \(\mathrm{x}, \mathrm{y}, \mathrm{z}\) coordinates of particle \(\# N\). In quantum mechanics, the momentum of a free particle is given by \(p=h / \lambda\), where \(h\) is Planck's constant. Only certain waves \(\Psi(x)\) are allowed in the box, such that \(\Psi(x)=0\) at the boundaries of the box, as shown in the figure below.
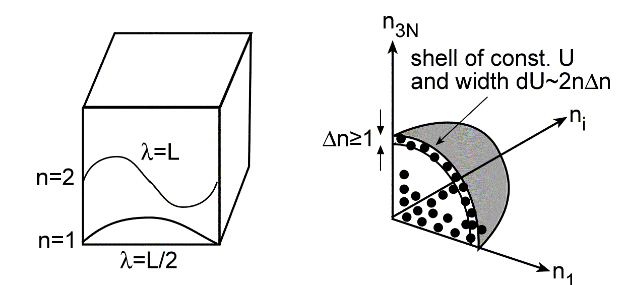
The wavelengths \(\lambda=\mathrm{L} / 2, \mathrm{~L}, 3 \mathrm{~L} / 2 \cdots\) can be inserted in the equation for total energy, yielding
\[U=\dfrac{1}{2 m} \sum_{i=1}^{3 N}\left(\dfrac{h n_{i}}{2 L}\right)^{2}=\sum_{i=1}^{3 N} \dfrac{h^{2} n_{i}^{2}}{8 m L^{2}}, \quad n_{i}=1,2,3 \cdots,\]
the energy for a bunch of particles in a box. W(U) is the number of states at energy U. Looking at the figure again, all the energy levels are "dots" in a \(3 \mathrm{~N}\)-dimensional cartesian space, called the "state space", or "action space" or sometimes "quantum number space." The surface of constant energy \(\mathrm{U}\) is the surface of a hypersphere of dimension \(3 \mathrm{~N}-1\) in state space. The reason is that the above equation is of the form constant \(=x^{2}+y^{2}+\cdots\) where the variables are the quantum numbers. The number of states within a thin shell of energy \(U\) at the surface of the sphere is
\[W(U) \; where\; \lim _{N \rightarrow \infty} W(U)=\tilde{\Omega}\].
\(\tilde{\Omega}\) is the total number of states inside the sphere, which at a first glance would seem to be much larger than W(U), the states in the shell. In fact, for a very high dimensional hypervolume, a thin shell at the surface contains all the volume, so in fact, \(\tilde{\Omega}\) is essentially equal to W(U) and we can just calculate the former to a good approximation when \(N\) is large.
If this is hard to believe, consider an analogous example of a hypercube instead of a hypersphere. Its volume is \(L^{\mathrm{m}}\), where \(m\) is the number of dimensions. The change in volume with side length \(\mathrm{L}\) is \(\partial \mathrm{V} / \partial \mathrm{L}=\mathrm{mL}^{\mathrm{m}-1}\), so \(\Delta \mathrm{V}=\mathrm{mL}^{\mathrm{m}-1} \Delta \mathrm{L}\) is the volume of a shell of width \(\Delta \mathrm{L}\) at the surface of the cube. The ratio of that volume to the total volume is \(\Delta \mathrm{V} / \mathrm{V}=\mathrm{m} \Delta \mathrm{L} / \mathrm{L}\). Let's take the example our intuition is built on, \(\mathrm{m}=3\), and assume \(\Delta \mathrm{L} / \mathrm{L}=0.001\), just a \(0.1 \%\) surface layer. Then \(\Delta \mathrm{V} / \mathrm{V}=3 \cdot 10^{-3}<<\mathrm{V}\) indeed. But now consider \(\mathrm{m}=10^{20}\), a typical number of particles in a statistical mechanical system. Now \(\Delta \mathrm{V} / \mathrm{V}=10^{20} 10^{-3}=10^{17}\). The little increment in volume is much greater than the original volume of the cube, and contains essentially all the volume of the new "slightly larger" cube. It may be "slightly" large in side length, but it is astronomically larger in volume.
Now back to our hypersphere in the figure. Its volume, which is essentially equal to W(U), the number of states just at the surface of the sphere, is
\[W(U)=\left(\dfrac{1}{2}\right)^{3 N} V_{\text {hypersphere }}=\left(\dfrac{1}{2}\right)^{3 N} \dfrac{\pi^{3 N / 2}}{\Gamma(3 N / 2+1)} R^{3 N}=\left(\dfrac{U}{U_{0}}\right)^{3 N / 2} .\]
The \((1 / 2)^{3 \mathrm{~N}}\) is there because all quantum numbers must be greater than zero, so only the positive part of the sphere should be counted. The Gamma function \(\Gamma\) is related to the factorial function, and \(R\) is the radius of the sphere, which is given by
\[R=n_{\text {max }}=\sqrt{\dfrac{8 m L^{2} U}{h^{2}}},\]
the largest quantum number, if all energy is in a single mode. They key is that \(R \sim \sqrt{U}\), so \(U\) is raised to the \(3 \mathrm{~N} / 2\) power, where \(N\) is the number of particles, 3 is because there are three modes per particle, and the \(1 / 2\) is because of the energy of a free particle depends on the square of the quantum number. Thus
\[S(U)=k_{B} \ln W(U)=S_{0}+\dfrac{3}{2} N k_{B} \ln U=S_{0}+\dfrac{3}{2} n R \ln U \text {, }\]
where the constant \(S_{0}\) is not the same as in the previous example. We used the volume equation from the previous example to obtain an equation of state (PV=nRT), and we can obtain another equation of state here:
\[\left(\dfrac{\partial S}{\partial U}\right)_{V, n}=\dfrac{1}{T}=\dfrac{3}{2} n R \dfrac{1}{U} \text { or } U=\dfrac{3}{2} n R T\]
This equation relates the energy of an ideal gas to its temperature. \(3 n\) is the number of modes or degrees of freedom (3 velocities per particle time \(n\) moles of particles), whereas the factor of 2 comes directly from the particle-in-a-box energy function - in case you ever wondered where that comes from. So, for a harmonic oscillator, \(\mathrm{n} \sim U\) \(\left(E=\hbar \omega(n+1 / 2)\right.\) as you may recall) instead of \(n \sim U^{1 / 2}\), and you might expect \(U=3 n R T\) for \(3 \mathrm{~N}\) particles held together by springs into a solid crystal lattice. And indeed, that is true for an ideal lattice at high temperature (in analogy to an ideal gas at high temperature). Unlike free particles, the energy of oscillators does not have the factor of 1/2. The 'deep' reason is that an oscillator has two degrees of freedom to store energy in each direction, not just one: there's still the kinetic energy, but there's also potential energy.
Example 3: A system of \(\mathrm{N}\) uncoupled spins \(\mathrm{s}_{\mathrm{z}}=\pm 1 / 2\)
The Hamiltonian for this system in a magnetic field is given by
\[H=\sum_{j=1}^{N} s_{z j} B+\dfrac{N B}{2} \text {, }\]
where the extra term at the end is added so the energy equals zero when all the spins are pointing down. At energy \(U=0\), no spin is excited. For each excited spin, the energy increases by \(B\), so at energy \(U, U / B\) atoms are excited. These \(U / B\) excitations are indistinguishable and can be distributed in \(\mathrm{N}\) sites:
\[W(U)=\dfrac{N !}{\left(N-\dfrac{U}{B}\right) !\left(\dfrac{U}{B}\right) !}=\dfrac{\Gamma(N+1)}{\Gamma\left(N+1-\dfrac{U}{B}\right) \Gamma\left(\dfrac{U}{B}+1\right)} .\]
This is our usual formula for permutations; the right side is in terms of Gamma functions, which are defined even when \(U / B\) is not an integer. Gamma functions basically interpolate the factorial function for noninteger values.
This formula has a potential problem built-in: clearly, when \(U\) starts out at 0 and then increases, \(W\) initially increases. But for \(U=N B\) (the maximum energy), \(W=1\) again. In fact, \(W\) reaches its maximum for \(U=N B / 2\). But if \(W(U)\) is not monotonic in \(U\), then \(S\) isn't either, violating P3 of thermodynamics. Let's see how this works out.
For large \(\mathrm{N}\), and temperature neither so low that \(\dfrac{U}{B} \sim O(1)\), nor so high that \(\dfrac{U}{B} \sim O(N)\), we can use the Stirling expansion \(\ln N ! \approx N \ln N-N\), yielding
\[\begin{aligned}
&\dfrac{S}{k_{B}}=\ln \Omega \approx N \ln N-N-\left(N-\dfrac{U}{B}\right) \ln \left(N-\dfrac{U}{B}\right)+N \dfrac{U}{B}-\dfrac{U}{B} \ln \dfrac{U}{B}+\dfrac{U}{B} \\
&\approx N \ln N-\left(N-\dfrac{U}{B}\right) \ln \left(N-\dfrac{U}{B}\right)-\dfrac{U}{B} \ln \dfrac{U}{B}+\dfrac{U}{B} \ln N-\dfrac{U}{B} \ln N \\
&\approx-N \ln \left(1-\dfrac{U}{N B}\right)+\dfrac{U}{B} \ln \left(1-\dfrac{U}{N B}\right)-\dfrac{U}{B} \ln \left(\dfrac{U}{N B}\right) \\
&\approx\left(\dfrac{U}{B}-N\right) \ln \left(1-\dfrac{U}{N B}\right)-\dfrac{U}{B} \ln \left(\dfrac{U}{N B}\right)
\end{aligned}\]
after canceling terms as much as possible. We can now calculate the temperature and obtain the equation of state \(U(T)\) :
\[\dfrac{1}{T}=\left(\dfrac{\partial S}{\partial U}\right)_{N} \approx \dfrac{k}{B} \ln \left(\dfrac{N B}{U}-1\right) \Rightarrow U \approx \dfrac{N B}{1+e^{B / k T}}\]
In this equations, at \(T \sim 0, \quad U \rightarrow 0\); and as \(T \rightarrow \infty, U \rightarrow N B / 2\). So even at infinite temperature the energy can only go up to half the maximum value, where \(W(U)\) is monotonic. The population cannot be 'inverted' to have more spins point up than down.
At most half the spins can be made to point up by heating. This should come as no surprise: if the number of microstates is maximized by having only half the spins point up when energy is added, then that's the state you will get (this is true even in the exact solution). Note that this does not mean that it is impossible to get all spins to point up. It is just not an equilibrium state at any temperature between 0 and \(\infty .\) Such nonequilibrium states with more spins up (or atoms excited) than down are called "inverted" populations. In lasers, such states are created by putting the system (like a laser crystal) far out of equilibrium. Such a state will then relax back to an equilibrium state, releasing a pulse of energy as the spins (or atoms) drop from the excited to the ground state.
The heat capacity of the above example system is
\[c_{v}=\left(\dfrac{\partial U}{\partial T}\right)_{N} \approx \dfrac{N B^{2}}{k T^{2}} \dfrac{e^{B / k T}}{\left(1+e^{B / k T}\right)^{2}} \text { peaked at } 4 k_{B} T / B \text {, }\]
so we can calculate thermodynamic quantities as input for thermodynamic manipulations. As we shall see in detail later (actually, we saw it in the previous example!), in any real system the heat capacity must eventually approach \(c_{v}=N k_{B} / 2\), where \(N\) is the number of degrees of freedom. However, a broad peak at \(4 k_{B} T / B\) is a sign of two low-lying energy levels spaced by \(B\). Levels at higher energy will eventually contribute to \(c_{v}\), making sure it does not drop.
Example 4: Let us check that T derived from
\[\left(\dfrac{\partial S}{\partial U}\right)_{N}=\left(\dfrac{\partial k_{B} \ln W}{\partial U}\right)_{N}=\dfrac{1}{T}\]
indeed agrees with the intuitive concept of temperature. Consider two baths within a closed system, so \(U=U_{1}+U_{2}=\) const. \(\Rightarrow d U=0 \Rightarrow d U_{1}=-d U_{2}\). If we know
\[W_{i}\left(U_{i}\right) \Rightarrow d W_{i}=\dfrac{\partial W_{i}}{\partial U_{i}} d U_{i}\]
for each bath, then
\[\begin{aligned}
W_{\text {tot }} &=W_{1} W_{2} \\
d W_{\text {tot }} &=\left(W_{1}+d W_{1}\right) \cdot\left(W_{2}+d W_{2}\right)-W_{1} W_{2}+O\left(d W^{2}\right) \\
&=W_{1} d W_{2}+W_{2} d W_{1} \\
&=\left(-W_{1} \dfrac{\partial W_{2}}{\partial U_{2}}+W_{2} \dfrac{\partial W_{1}}{\partial U_{1}}\right) d U_{1}=0
\end{aligned}\]
at equilibrium because the maximum number of states is already occupied. For this to be true for any infinitesimal energy flow \(d U_{1}\),
\[\begin{aligned}
&\Rightarrow \dfrac{1}{W_{2}}\left(\dfrac{\partial W_{2}}{\partial U_{2}}\right)_{V, N}=\dfrac{1}{W_{1}}\left(\dfrac{\partial W_{1}}{\partial U_{2}}\right)_{V, N} \\
&\Rightarrow\left(\dfrac{\partial \ln W_{2}}{\partial U_{2}}\right)_{V, N}=\left(\dfrac{\partial \ln W_{1}}{\partial U_{2}}\right)_{V, N} \text { or }\left(\dfrac{\partial S_{2}}{\partial U_{2}}\right)_{V, N}=\dfrac{1}{T_{2}}=\left(\dfrac{\partial S_{1}}{\partial U}\right)_{V, N}=\dfrac{1}{T_{1}}
\end{aligned}\]
At equilibrium, the temperatures are equal, fitting out thermodynamic definition that "temperature is equalized when heat flow is allowed."

