10. Postulates of statistical mechanics
- Page ID
- 9169
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Thermodynamics puts constraints on the behavior of macroscopic systems without referencing the underlying microscopic properties. In particular, it does not provide a quantitative connection to the origin of its fundamental quantities \(U\) and \(S\). For \(U\), this is less of a problem because we know from mechanics that
\[ U=\dfrac{1}{2} \sum m_i v_i^2 + V(x_i),\]
and the macroscopic formula arises by integrating over most coordinates and velocities. Somehow the thermal motions end up as \(TS\), and the mechanical and electrical motions end up as terms such as \(–PV+\mu n\).
Statistical mechanics makes the macro-micro connection and provides a quantitative description of U and S is terms of microscopic quantities. For large systems (except near the critical point), its results are in agreement with thermodynamics: one can derive thermodynamic postulates 0 – 3 from statistical mechanics. For systems undergoing large fluctuations (small systems or those systems near a critical point), its prediction are different and more accurate.
In addition as the ‘mechanics’ implies, statistical mechanics can deal with time-varying systems and systems out of equilibrium. Averages over x(t) and p(t)=mv(t) of the microscopic particles are done, but not in such a way that all time-dependent information is lost, as in thermodynamics.
Unlike mechanics, statistical mechanics is not intended to discuss the time-dependence of an isolated particle. Rather, the time-dependent (e.g. diffusion coefficient) and time independent properties of whole systems of particles, and the averaged properties of whole ensembles of such systems, are of interest.
We begin with an introduction to important facts from mechanics and statistics, then proceed to the postulates of statistical mechanics, consider in detail equilibrium systems, and finally non-equilibrium systems.
Goal of statistical mechanics:
- have a system of many particles with positions \(x_{i}\) and velocities \(\dot{x}_{i}\) (or wavefunctions \(\Psi\left(x_{i}\right)\).
- want values \(\mathrm{A}(\mathrm{t})\) of any observable \(A\left(x_{i}, \dot{x}_{i}\right)\) as particles move about, averaged over all microstates of the system consistent with constraints, such as energy \(=\mathrm{U}=\) constant, or \(\mathrm{V}=\) constant.
Goal of thermodynamics:
- find relations among extensive observables \(X\) and their derivatives at equilibrium only.
The postulates of statistical mechanics and connection to thermodynamics:
Postulate I: Extension of microscopic laws
Hamiltonian dynamics applies to the density operator \(\hat{\rho}_{i}\) of any finite closed system; fully specified by its extensive constrainnt parameters and the Hamiltonian.
Postulate II: Principle of equal probabilities
The principle of equal probabilities holds in its ensemble (weak) form and is assumed in it strong (time) form
i) weak form: all W microscopic realizations of a system satisfying I have equal probability. The ensemble density matrix is therefore given by \(\hat{\rho}=\frac{1}{W} \sum_{i=1}^{W} \hat{\rho}_{i}\). The ensemble of these \(W\) systems is the microcanonical ensemble.
ii) strong form: for any ensemble satisfying i) at equilibrium,
\(\left\langle\hat{\rho}_{i}\right\rangle_{t}=\left\langle\hat{\rho}_{i}\right\rangle_{e}=\hat{\rho}\) (ergodic principle). This states that averaging over time is equivalent to averaging over the ensemble of \(\mathrm{W}\) microstates.
Postulate III: entropy
The entropy of a n ensemble of systems satisfying postuilates I and II.i) is given by \[S=-\operatorname{Tr}\{\hat{\rho} \ln \hat{\rho}\}\]
Before we use them, these postulates require some explanation.
I) This is a strong statement; the system i usually has a \(>10^{20}\)-dimensional phase space, and we assume that the dynamics are the same as for a few degrees of freedom! Classically, \(\hat{\rho}_{i}\) corresponds to a specific trajectory; quantum mechanically, to a specific initial condition of the system. Among the extensive variables fixed in a closed finite system: U (always by postulate I). Other constrained variables: \(\mathrm{V}\) (or \(\mathrm{L}, \mathrm{A}, \mathrm{N}_{\mathrm{i}}=\) particle number ... depending on the system).
Note that if \(\hat{H}\) is independent of time, the system is closed, and \(U\) is therefore constant (as it needs to be for 'full' specification of the system), P1 of thermodynamics is automatically satisfied.
II) This is the postulate that lets us perform macroscopic averages over the individual density matrices, so we can derive properties for the energyconserving (microcanonical) ensemble.
i. Classically, this says that as long as a trajectory stratifies the constraints in I (has specific energy U), we can combine it with equal weight with all other such trajectories to obtain \(\rho\left(q_{i}, p_{i}, t\right)\), the classical density function.
Quantum-mechanically, this means that all the linearly independent pure density matrices \(\hat{\rho}_{i}\) characterizing a system with the same extensive parameters (i.e. all the members of the microcanonical ensemble) can be averaged with equal weights to obtain the ensemble density matrix.
Example:
consider a state of energy \(U\) that can be realized in \(W\) ways (W-fold degenerate or W microstates). One set of initial conditions \(\hat{\rho}_{i}\) would be
\[\rho_{1}=\left(\begin{array}{ccc}
1 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0
\end{array}\right), \rho_{2}=\left(\begin{array}{ccc}
0 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 0
\end{array}\right), \ldots\]
These are pure states. All of these are equally likely because they have the same energy (and volume, etc.), so
\[\hat{\rho}=\frac{1}{W} \sum_{i=1}^{W} \hat{\rho}_{i}=\left(\begin{array}{ccc}
1 / W & & 0 \\
& \ddots & \\
0 & & 1 / W
\end{array}\right)\]
This is a 'mixed' sate of constant energy U.
Note that there is a potentially embarrassing problem with this: a finite quantum system (e.g. particle in a box) for which all extensive parameters (e.g. \(U\), or \(L\) for particles in a 1-D box) have been specified has as discrete energy spectrum given by \(H\left|\varphi_{i}\right\rangle=E_{i}\left|\varphi_{i}\right\rangle .\) For a large system, the level spacing may be very narrow, but it is nonetheless discrete. Thus, at some every U we pick, there is likely to be no state, so we have nothing to average!
In practice, this is resolved by having an energy window \(\delta U\), and by considering all W levels within it. As discussed in more detail in III below, as the number of degrees of freedom \(N=6 n\) of the system approaches infinity, the size of \(\delta U\) rigorously has no effect on the result.
ii. This says we could take a single trajectory, or a single initial condition \(\hat{\rho}_{i}(0)\), propagate it in time, and all the possible microscopic states will also be visited in turn to yield again \(\rho\left(q_{i}, p_{i}, t\right)\) (classically) or \(\hat{\rho}(t)\) (quantum mechanically). This is a much stronger statement than i): the full ensemble of W microstates by definition includes all realizations i of the macroscopic system compatible with \(\mathrm{H}\) and the constraints; on the other hand ii) says a single microstate will, in time, evolve to explore all the others, or at least come arbitrarily close to them. This property is know as 'ergodicity.' In practice, ergodicity cannot really be satisfied, but we can use ii) for 'all practical purposes.'
Example showing why ergodicity cannot be satisfied:
We will use a discrete system to illustrate. Consider a box with \(M=\frac{V}{V_{0}}\) cells, filled with \(N \ll M\) particles of volume \(V_{0}\). The dynamics is that the particles hop randomly to unoccupied neighboring cells at each time step \(\Delta t\). This model is crlled a hatice ideal gas. The number of arrangementsfor \(N\) identical particles
\[W=\frac{M!}{(M-N) !} \cdot \frac{1}{N!}\]
Large factorial n! (or gamma fuactious \(\Gamma (n-1)-N!)\) can be approximated by
\[W=\frac{M!}{(M-N) !} \cdot \frac{1}{M!} \cdot M^{M}(M -N)^{N-M} M^{M}=\left(\frac{M}{N}\right)^{N}\]
Let us plug realistic numbers into this
\(V_{0}=10 \hat{A}_{o}\), V=1 cm3, \( \rightarrow M=\frac{V}{V_{0}}=10^{23}\).
For N ~ 1019 gas molecules (~1 atm) \( \rightarrow\) M/N =104
\( v_{gas}=\left ( \frac{U_{o}}{m} \right )= 300 m/s \) (O2 at room temperature)
\( \Delta t= \frac{L_{o}}{v} = \frac{V_{o}^{1/3}}{v} =10^{-12}s = 1\;ps \)
\( W_{possible}= \frac{10^{12}s}{10^{18}s}=10^{30} \)
Lifetime of universe: \( \leqslant 10^{11} a \ldots 10^{18} s\)
\(W_{\text {actual }}\) = \(\left(10^{4}\right)^{10^{19}}=\) 1 googol \( \geqslant 10^{30}\)
The possible \(W\) that can te visited during the lifetime of the universe is a mere 1030, negligible compared to the actual rnumber of microsta Wactual at constant energy
Clearly, not even a warm gas, a system about as random as conceivable, even touches the true microcanonical degeneracy W. Although the a priori probability of microstates (classically: of trajectories) may be the same (i), they simply cannot all be sampled in finite time as seen in (iii), this provides a practical solution to the quantum dilemma outlined in (i)
Why assume (ii) at all? In real life \(\hat{\rho}_{i}(t) \) is always observed, but it is difficult to compute. W or \(\hat{\rho}(t) \) are often much easier to compute. Although (ii) fails by a factor, surprisingly it still works in most situations: most microstates in the ensemble of Wpossible microstates are indistinguishable(e.g. the gas atoms in the room right now vs 10 seconds from now), so leaving many of them out of the average still yields the same average; sampling only one in 1027 still gives the same result as true ensemble averaging.
There are cases where this reasoning fails: in glasses, members of the ensemble can be so slowly interconnecting and so different from one another, that \(\hat{\rho}\) is not at all like \(\left\langle\rho_{i}\right\rangle_{t}\) unless very special care is taken.
III) This definition of the entropy was made plausible in our mathematical review, on grounds of information content: a system with many microstates has a greater potential for disorder than a system of a few microstates. But instead of measuring disorder multiplicatively, we want an additive (extensive) quantity. This postulate proves the microscopic definition for thermodynamic entropy \(\left(\hat{\rho}=\hat{\rho}_{e q} \& N \rightarrow \infty\right)\), just as energy is microscopically defined as
\[U=\langle H\rangle_{e} \text { where } H=\frac{1}{2} \sum_{j} \frac{p_{j}^{2}}{m_{j}}+V\left(x_{i}\right)\]
so
\[S_{e q} \equiv S=-k_{B} T_{r}\left\{\hat{\rho}_{e q} \ln \hat{\rho}_{e q}\right\}\]
gives the thermodynamic entropy \(S\) in terms of the equilibrium density matrix. We must have \(\operatorname{Tr}\left\{\hat{\rho}_{e q}\right\}=1,\left[\hat{\rho}_{e q}, H\right]=0\), and by postulate II.i), all elements of \(\hat{\rho}_{e q}\) must be of equal size if we are in the microcanonical (constant energy U) ensemble. This is satisfied only by
\[\hat{\rho}_{e q}=\left(\begin{array}{ccc}\frac{1}{W} & & 0 \\0 & & \frac{1}{W}\end{array}\right)\]
Where \(\hat{\rho}\) is a diagonal \(\mathrm{W} \times \mathrm{W}\) matrix. Inserting into \(\mathrm{S}\) and evaluating the trace in the eigenfunction basis of \(\hat{H}\) (and \(\hat{\rho}\) ), which we can call \(|j\rangle:\)
\[\begin{aligned}&S=-k_{B} \sum_{j=1}^{W}\left\langle j\left|\hat{\rho}_{e q} \ln \hat{\rho}_{e q}\right| j\right\rangle=-k_{B} \sum_{j=1}^{W} \frac{1}{W} \ln \frac{1}{W} \\
&\Rightarrow S=k_{B} \ln W \quad \text { where } k_{B} \approx 1.38 \cdot 10^{-23} J / K \text { is Boltzmann's constant. }
\end{aligned}\]
This is Boltzmann's famous formula for the entropy. Postulate III is more general, but at equilibrium Boltzmann's formula holds. It secures for \(\mathrm{S}\) all the properties in postulates 2 and 3 of thermodynamics, and provides a microscopic interpretation for \(\mathrm{S}\) :
W specifies disorder in a system: the more possible microstates correspond to the same macrostate, the more disorder a system has. For two independent systems, \(W_{\text {tot }}=W_{\mathrm{i}} \cdot W_{2} .\) However, thermodynamic entropy has the property of additivity: \(S_{\text {tot }}=S_{1}+S_{2}\). The function that uniquely effects the transformation from multiplication to addition is the log function (within a constant factor) \(\Rightarrow S_{i}=\ln W_{i}\) must be true so that both relations at the beginning of this
paragraph are satisfied. The constant factor \(k_{\mathrm{B}}\) is provided to match the energy and temperature scales, which were independently defined in the early \(19^{\text {th }}\) century when the equivalence of temperature and average energy was not understood.
Consider a system divided into subsystems by constraints, with \(W=W_{0} .\) When the constraints are removed at \(t=0\), then by II.ii) the system now explores additional ensemble members as time goes on. Thus \(\mathrm{W}(\mathrm{t}>0)=\mathrm{W}_{1}>\mathrm{W}_{0}\). If macroscopic equilibrium is reached \(W_{e q}>W_{1}>W_{0} \Rightarrow S_{e q}>S_{0}\).
Thus S in stat mech postulate III satisfies all requirements of postulate P2 of thermodynamics, which is a simple consequence of the fact that microscopic degrees of freedom tend to explore all available states (= all the available phase space in classical mechanics).
Also, because \(W\) is monotonic in \(U\) (at higher energy \(U\), there are always more quantum states in a multidimensional system) and because \(S\) is monotonic in \(W\) (property of the ln function), \(S\) is monotonic in \(U\). finally, we shall see in detail later that when \(\left(\frac{\partial U}{\partial S}\right)_{V, N}=T\), only the ground state is populated, so \(W \rightarrow 1 \Rightarrow \lim _{T \rightarrow 0} S=k_{B} \ln (1)=0\). Thus, the third postulate is also satisfied as long as the ground state is singly degenerate and the system can get to it during the experiment. (Glasses again would be a problem here!)
The error of thermodynamics: it identifies the most probable value of a quantity with its average, by assuming the spread is negligible. We will derive examples of this spread later on. Thermodynamic limit: \(\mathrm{N}\) goes to infinity but \(\mathrm{N} / \mathrm{V}\) or any other ratio of extensive quantities remains constant.
To conclude this chapter, we turn to the problem of computing \(W\) in the quantum case. A closed finite quantum system has a discrete spectrum \(\mathrm{E}_{i}\). The figure below shows the number of states below energy \(U\) as a function of \(U\). Because of quantum mechanics, the density of states
\[\Omega(U)=\frac{\partial \tilde{\Omega}}{\partial U}\]
is discontinuous, and the integrated density of states (= total number of states up to energy \(U\) ) has steps in it:
\[\tilde{\Omega}=\sum_{j} \operatorname{Step}\left(U-E_{j}\right) \Rightarrow \Omega=\sum_{j} \delta\left(U-E_{j}\right)\]
At any randomly picked \(U, \Omega\) is mostly likely zero, so \(W=0\) also!
However, because \(\Omega\) increases so enormously rapidly with energy, the states are very (understatement!) closely spaced in energy for any system with even just a few particles. If a system is observed for a finite time \(\delta t\), the states are broadened by the uncertainty principle:
\[\delta E \sim \frac{\hbar}{2 \delta t} \Rightarrow \Omega=\sum_{i} L_{i}\left(U-E_{i}, \delta t\right)\]
where \(L\) indicates a broadened profile of finite width that replaces the delta function. L still counts a single state, so \(\int_{0}^{\infty} d U L_{i}\left(U-E_{i}, \delta t\right)=1 ;\) often \(L_{i}\) is taken as a Lorentzian \(L_{i}=\frac{1}{\pi} \frac{\delta U}{\left(U-E_{i}\right)^{2}+\delta U^{2}} .\) Thus, \(\Omega\) can be taken as a smooth function and its value \(\Omega(E, \delta t)=W(U)\) tells us how many states contribute to the degeneracy at energy U.
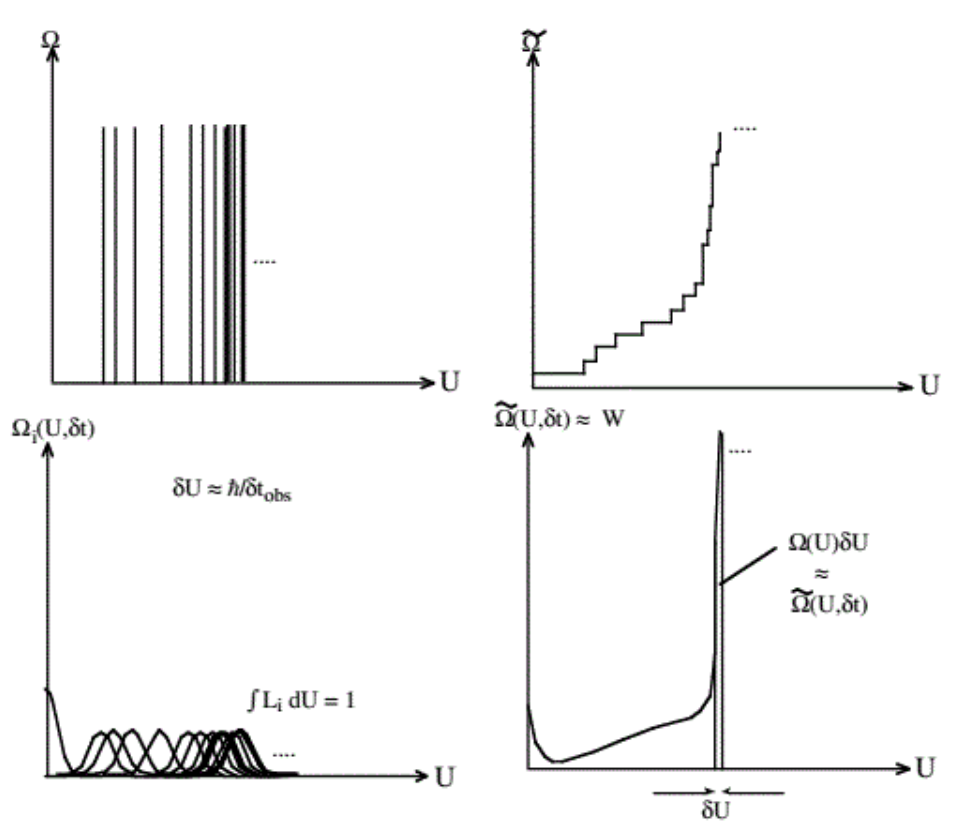
It is clear from the above that if \(\delta U \gg\left|E_{j}-E_{i}\right|\), (the broadening is greater than the spacing of adjacent levels), then \(\Omega(U)\) is indeed independent of the choice of \(\delta U\) or \(\delta t\). This is guaranteed by the astronomical number of states for a macroscopic system (see example in II.ii)). Because \(\tilde{\Omega}\) in the above figure grows so fast, \(\Omega(U) \delta U \approx \tilde{\Omega}(U)\), as illustrated in the bottom right panel of the figure
Another way to look at it is in state space (classically: action space). It has \(\mathrm{N}\) coordinates for \(\mathrm{N}\) degrees of freedom. \(\tilde{\Omega}\) is the number of states under the surface \(\mathrm{U}\) \(=\) constant. If \(U \gg U_{0}\) (where \(U_{0}\) is the average characteristic energy step for one degree of freedom) then
\[\tilde{\Omega}_{1} \sim\left(\frac{U}{U_{0}}\right)^{N}\]
Letting \(\delta U\) now be an uncertainty in U instead of in individual energy levels, the number of states in the interval \((U-\delta U, U)\) is
\[
\tilde{\Omega}(U)-\tilde{\Omega}(U-\delta U) \sim\left(\frac{U}{U_{0}}\right)^{N}-\left(\frac{U-\delta U}{U_{0}}\right)^{N} \approx\left(\frac{U}{U_{0}}\right)^{N}\left\{1-\left[1-\frac{\delta U}{U}\right]^{N}\right\} \approx\left(\frac{U}{U_{0}}\right)^{N}
\]
Because \(\mathrm{N} \sim 10^{20}\), as long as \(\delta U<U\) (even if only a small amount!), the number of states in any width shell \(\delta U\) is the same as the total number of states up to U:
In a hyperspace of \(10^{20}\) dimensions, all states lie near the surface
Thus \(\tilde{\Omega}(U) \approx \Omega(U, \delta U) \approx W(U)\) to extreme precision. This topic will be taken up once more in the examples of microcanonical calculations given in the next chapter.

