XAS - Theory
- Page ID
- 1871
XAS, or X-ray Absorption Spectroscopy, is a broadly used method to investigate atomic local structure as well as electronic states. Very generally, an X-ray strikes an atom and excites a core electron that can either be promoted to an unoccupied level, or ejected from the atom. Both of these processes will create a core hole. If the electron dissociates, this produces an excited ion as well as photoelectron and is studied by X-ray Photoelectron Spectroscopy (XPS).
Introduction
The electrons that are excited are typically from the 1s or 2p shell, so the energies are on the order of thousands of electron volts. XAS therefore requires high-energy X-ray excitation, which occurs at synchrotron facilities. X-ray energy is about 104 eV (where "soft x-rays" are between 100 eV- 3 keV and "hard x-rays" are above 3 keV) corresponding to wavelengths around 1 Angstrom. This wavelength is on the same order of magnitude as atom-atom separation in molecular structures, so XAS is a useful tool to deduce local structure of atoms. XAS is also utilized in analyzing materials based on their characteristic X-ray absorption "fingerprints." It is possible to deduce local atomic environments of each separate type of atom in a compound. XAS is particularly convenient because it is a non-destructive method to examine samples directly. Structures can be determined from samples that are both heterogeneous and amorphous.
When an X-ray strikes an atom, one of the core electrons is either excited to a higher energy unoccupied state (a transition studied by XAS) or into an unbound state, called the continuum. When electrons are ejected from an atom of a solid material, this is essentially the photoelectric effect and is studied by X-ray Photoelectron Spectroscopy. Below is a diagram illustrating an atom absorbing an x-ray with the resultant ejection of a core electron into the continuum. Note that the level K refers to the n=1 level, L refers to the n=2 level, and M refers to the n=3 level.
The wave vector of a photoelectron
Determining the wave vector of the electron dictates which subset of XAS will be used (EXAFS, NEXAFS, etc.). The kinetic energy \(E_k\) and threshold energy \(E_0\) (amount of energy the photoelectron needed to promote the electron into the continuum) of the photoelectron can be addressed, after considering the de Broglie equation:
\[\lambda = \dfrac{h}{p}\]
where
- \(p\) is the momentum of the electron,
- \(\lambda\) is the wavelength, and
- \(h\) is Planck’s constant.
The wave vector of the electron is denoted as k, and can be defined as
\[ k = \dfrac{2\pi}{\lambda} = \dfrac{2\pi p}{h}\]
and thus the electron kinetic energy is written
\[\mathrm{E}_{\mathrm{k}}=\frac{1}{2} \mathrm{mv}^{2}=\frac{1}{2}\left(\frac{\mathrm{p}^{2}}{\mathrm{m}}\right)=\left(\frac{\mathrm{h}}{2 \pi}\right)^{2} \frac{\mathrm{k}^{2}}{2 \mathrm{m}}\]
In terms of the incident x-ray energy, \(E\), and the threshold energy \(E_0\),
\[\mathrm{E}_{\mathrm{k}}=\mathrm{E}-\mathrm{E}_{0}=\mathrm{h} \nu-\mathrm{E}_{0}\]
The expression for the wave vector \(k\) of the photoelectron can thus be written as
\[k=\sqrt{\left(\frac{2 \pi}{h}\right)^{2} 2 m\left(h v-E_{o}\right)}\]
Depending on values of k, different subsets of XAS will be used. For example, if \(k=0\), or if \(0<k<2/R\) (where \(R\) is the distance between the x-ray absorbing atom and it’s nearest neighbor), low-energy Near Edge X-ray Absorption Fine Structure (NEXAFS) and NEXAFS will be used, respectively. If \(k>k_c\), where \(k_c\) is equal to \(2/R\), Extended X-ray Absorption Fine Structure (EXAFS) is used. It is apparent from the diagram below that there are three different types of excited photoelectrons upon absorption of an x-ray quantum. For the sake of completeness, these are briefly discussed below.
The first type of photoelectron transition to an unoccupied valence state, as it does not have enough energy to completely leave the atom. The second type of photoelectron actually has just enough kinetic energy to be able to escape into the continuum. Multiple scattering processes occur here, between multiple surrounding atoms that neighbor the absorbing atom. Lastly, the third type of photoelectron has a very high kinetic energy, and weak back-scattering occurs in a single scattering process between only one neighbor atom.
Returning to the formula for the kinetic energy of an electron
\[\mathrm{E}_{\mathrm{k}}=\mathrm{E}-\mathrm{E}_{0}=\mathrm{h} v-\mathrm{E}_{0}\]
can be rewritten as
\[E_{k}=h v-E_{B}-\phi\]
Here, \(E_B\) is the binding energy of the core electron to the atom, while the expression \(E_B + \phi\) is the ionization energy. A more in-depth analysis of the ionization energy can be found in the section regarding Koopman's theorem.
Beer’s Law and the relation to XAS
Beer's Law can be applied to XAS for an x-ray beam that is both narrow and monochromatic, striking the absorber at a 90 degree angle. The absorber has a uniform composition and thickness. The important result of this derivation will be an expression describing the absorption coefficient, \(\mu_M\), of X-ray absorption. Beginning with the basic model of
Beer’s law can be written
\[\log \left(\frac{I_{1}}{I_{2}}\right)=k \Delta m=k_{d} \Delta d\]
where m and d refer to the mass and thickness of the sample, respectively. The terms k and \(k_d\) are proportionality constants whose units are dependent on the units of m or d, the wavelength, and also the elements comprising the sample. The previous equation can be written in terms of natural logarithms, in which case
\[\log \left(\frac{I_{1}}{I_{2}}\right)=\mu_{M} \Delta m=\mu_{M} \rho \Delta d\]
where the symbol \(\mu_M\) has been introduced, and is termed the mass absorption coefficient. Units of \(\mu_M\) are cm2/g, and amounts are not dependent on the physical or chemical state of the element as X-ray absorption is primarily an atomic property. The term \(\Delta m\) is the mass difference of two samples in units of g/cm2 of irradiated sample area, and \(\Delta d\) is the thickness of the sample in units of centimeters. Density of the sample is \(\rho\) in units of g/cm3. This equation is limited to the sample area receiving uniform radiation by the X-ray beam. In thickness measurements, the linear absorption coefficient ?l is introduced, and the previous equation can be written
\[\ln \left(\frac{l_{1}}{l_{2}}\right)=\mu_{b} \Delta d\]
The linear absorption coefficient has a characteristic value depending on both the element and the quantity of atoms that are in the beam path. The value of \(\Delta d\) is the thickness of the sample that is irradiated in units of centimeters. It is obvious that
\[\mu_{1}=\mu_{\mathrm{M}} \rho\]
Furthermore, one can define the atomic mass absorption coefficient that measures the “cross-section” of the absorbing atom as
\[\mu=\mu_{\mathrm{M}} \frac{\mathrm{M}}{\mathrm{N}}\]
where M is the absorbing atom’s atomic mass and N is Avogadro’s number. Values of \(\mu_M\) for a sample can be calculated using
\[\mu_{M}=W_{A} \mu_{A}+W_{B} \mu_{B}+W_{C} \mu_{C}+\ldots\]
where the sample contains elements A, B, and C of weight fractions \(W_A\), \(W_B\), and \(W_C\), and mass absorption coefficients of \(\mu_A\), \(\mu_B\), and \(\mu_C\). Values of \(\mu_A\), \(\mu_B\), and \(\mu_C\) at different wavelengths are available in many sources. As stated previously, the value of the mass absorption coefficient is primarily an atomic property. It is not dependent on the state of the atom; for instance, a bromine atom in the form of vapor, potassium bromide or sodium bromate, liquid or solid bromide, has the same chance of absorbing an x-ray quantum in all of these forms.
More on the absorption coefficient, \(\mu_M\)
At higher photon energies, \(\mu_M\) decreases steadily. However, when the necessary energy for a core electron transition is achieved, \(\mu_M\) increases sharply and causes an absorption edge. This occurs when the photon energy just matches the energy needed to either promote a core electron into an empty valence level, or to completely eject the electron from the atom (electron is promoted into the continuum). Each edge occurs at its own critical absorption wavelength. The associated energies are the electron binding energy in the K, L, and M… shells (based on the Bohr atomic model, \(n=1\) for \(K\) edges, \(n=2\) for \(L\) edges, \(n=3\) for \(M\) etc.) of the particular atom absorbing the X-rays.
The resultant spectrum of a sample will show these edges at the X-ray photon energies that equal the ionization potentials of the bound electrons in the component atoms. Seen in the figure below are the K-edge and three L-edges of a typical X-ray absorption spectrum. This nomenclature indicates which core orbital the electron originated from. The K-edge is a consequence of the 1s – 3p transition, where the L-edges are from 2s – 5p (\(L_I\)), \(2p_{1/2} – 5d_{3/2}\) (\(L_{II}\)), and \(2p_{3/2} – 5d_{5/2}\) (\(L_{III}\)) transitions. Elements have characteristic edges, a few of which can be seen in Table 1.
There are a few factors that directly influence the exact energy of the edge. The charge density of the absorbing atom is very important, and is itself influenced by the valence or oxidation state. The energy of the X-ray absorbing edge is proportional to the oxidation state of the absorbing atom; the edge will occur at a higher energy the more positive the oxidation state of the atom. This can be simply explained by considering that it is increasingly difficult to remove an electron from an atom that bears a higher positive charge.
Another factor influencing the edge energy is the atomic number of the absorbing atom. As atomic number increases, so does the corresponding edge energy. A plot of the energy of the edge as a function of atomic number can be seen below. The X-ray photon energy region of approximately 2-30 keV limits the accessible \(K\) edges. Because current synchrotron sources do not produce high intensity X-ray energies greater than 30 keV, elements P to Sn can be analyzed, but anything past this cannot. The energy required to separate a 1s electron from elements of atomic numbers greater than \(Sn\) is too high for current synchrotron sources. However, because L edges occur at lower energies than \(K\) edges, it is possible to examine the rest of the elements using XAS. Lr, the heaviest element, has an \(L_{III}\) edge occurring at 22 keV, an energy that synchrotrons can indeed produce.
Koopman's Theorem and the relation to x-ray absorption
As stated previously, x-ray absorption is capable of exciting and dissociating a core electron from a neutral atom. This aspect of x-ray absorption is studied by XPS, but we will discuss this here for completeness. Calculating the energy for this ionization potential is of interest. Koopman’s Theorem (KT) is a method that relates experimental ionization potentials to the molecular orbital energy levels. Considering an orbital ?i of energy \(E_i\), Koopman’s Theorem says that the value of \(–E_i\) is equal to the ionization potential needed to remove an electron from ?i. Stated differently, the ionization potential is the negative value of the HOMO energy. Koopman’s Theoroem is an application of the Hartree-Fock approximation, as the value of \(E_i\) is calculated via the HF approximation. This is the simplest method to evaluate ionization potentials.
Koopman’s theorem assumes that a multi-electron atom has an electronic wavefunction which can be described using a Slater determinant. The Slater determinant is a set of one-electron wavefunctions, where each wavefunction in the determinant is the eigenfunction of the related Fock operator. Another assumption made is that when an electron is added or removed from the system, the remaining electrons’ corresponding Fock operators do not change. Thus the Koopman’s theorem predicted value of a final wavefunction has a higher energy than the actual final wavefunction. This is because in reality an addition or removal of an electron to or from the initial wavefunction will change the system’s Fock operator. This would result in a re-organizing of the one-electron wavefunctions, which Koopman’s theorem disregards.
Koopman’s theorem uses the Hartree-Fock theory in describing the value of \(E_i\), where the Hartee-Fock theory describes ionization or electron-gain of a system. A more accurate method would be electron correlation, which is typically calculated by post Hartree-Fock methods.
A review of the Hartree-Fock Approximation
Assume that a single Slater determinant can describe the closed-shell system having \(N\) electrons. The Slater determinant, \(|\psi_i\rangle\), can be written as a set of \(N\) orthonormal spin orbitals, \(\chi_1\), \(\chi_2\),…\(\chi_N\).
\[\left|\psi_{0}\right\rangle=\left|\chi_{1}, \chi_{2}, \ldots, \chi_{N}\right\rangle\]
Recall that the Hartree-Fock method seeks to find the spin orbital \(Y_0\) that minimizes \(E_0\), using the electrostatic Hamiltonian, H, operating on \(|\psi_0\rangle\).
\[E_{0}=\left\langle\psi_{0}|H| \psi_{0}\right\rangle=\sum_{i=1}^{N}\langle i|h| i\rangle+\frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N}\{[i i | j j]-[i j \beta j]\}\]
where
\[\langle i|h|i \rangle = \langle\chi_i|h|\chi_j\rangle = \int dx_1\chi_1*(x_1)h(x_1)\chi_j(x_1)\]
\[\left[ ij|kl\right] = \left[\chi_i\chi_j|\chi_k\chi_l\right] = \int dx_1dx_2\chi_i^*(x_1)\chi_j(x_1)\frac{1}{r_{12}}\chi_k^*(x_2)\chi_l(x_2)\]
and \(h(x_1)\) is the usual one-electron core-Hamiltonian. Based on the minimization condition on \(E_0\), the following expression can be recognized, where the occupied spin orbitals ? span a subspace of the Fock operator, \(f\).
\[f\left|\chi_{n}\right\rangle=\sum_{j=1}^{N} \varepsilon_{\omega}\left|\chi_{3}\right\rangle\]
This holds true for any a from 1,2,3….N. Also, the Fock operator matrix elements between occupied spin orbitals and virtual spin orbitals must be zero. If there is a set of N spin orbitals that satisfies the previous equation, and which has a unitary transformation performed on it, then a new set of spin orbitals will be produced that satisfy the same equation. The unitary transformation is chosen such that the matrix will have diagonal elements of
\[\epsilon_{ij}=\langle\chi_i|f|\chi_j\rangle\]
The corresponding spin orbitals are referred to as "canonical spin orbitals." Also, the Fock operator is defined as
\[\langle\chi_i|f|\chi_j\rangle = \langle\chi_i|h|\chi_j\rangle + \sum^N_{k=1}{[ij|kk]-[ik|kj]}\]
Evaluating the Ionization Potential
The energy needed to remove an electron from an atom can now be evaluated. To get a close approximation of the ionization potential, the neutral and ionic states require a good description. The neutral state is said to be at the HF level. A rough assumption can be made with respect to the electron density of the ionic system. The ionic system has an electron density of the neutral system minus the density of the orbital from which the electron has been removed. A “frozen orbital” approximation has been used here, in that it is assumed the other N-1 electrons do not change their spatial distributions upon ionization. Thus the ionic molecule can be described using the neutral molecule’s Hartree-Fock spin orbitals.
To summarize thus far,
- The value of \(E_0\) is the HF energy of an N-electron system.
- The HF canonical spin orbitals of the N-1 electron system are used to build up the mean value of H over an N-1 electron single determinant.
Koopman's theorem thus says that the difference between \(E_0\) and the mean value of H is a good approximation of the ionization potential of the corresponding N-electron system. If the ionization system is described by the N-1 -electron single determinant, and the canonical HF spin orbitals of the neutral system are ?\(\chi_i\), then it is possible to write an expression for the ionization potential as
\[-\epsilon_{cc}={}^{(N-1)}E_c - {}^NE_0 = \left\langle{}^{(N-1)}\Psi_c|H|{}^{(N-1)}\Psi_c\right\rangle - \left\langle{}^N\Psi_0|H|{}^N\Psi_0\right\rangle\]
where
\[|{}^{N-1}\Psi_c\rangle = |\chi_1\chi_2,\dots,\chi_{c-1},\chi_{c+1},\dots,\chi_N\rangle\]
The matrix element \(\epsilon_{cc}\) is an eigenvalue of the Fock matrix if one uses the canonical spin orbitals in the calculation. Koopman showed that the use of the canonical spin orbitals as HF spin orbitals produce the lowest energy of the ion. Thus it is possible to approximate the ionization potentials by the eigenvalues of the Fock matrix.
Fermi's Golden Rule applied to XAS
Analysis of both the initial and final states of the absorbing atom is necessary to determine the probability of a core electron to absorb an x-ray photon. XAS measures the transition of an electron initially in a deep core state and finally in a previously unoccupied state. Fermi’s golden rule gives the transition probability, to which the x-ray absorption coefficient is proportional. This relationship can be expressed as
\[\mu(E)\sim\sum_f|\langle\psi_i|A(r)\cdot p|\psi_f\rangle|^2\delta(E-E_f)\]
where the photoelectron energy is E=?? – \(E_i\). \(\psi_i\) and \(\psi_f\) are the initial and final eigenstates and have energies \(E_i\) and \(E_f\). The initial state is the ground state of the atom. These wavefunctions are typically calculated using a Self-Consistent Field (SCF) approximation. The coupling to the x-ray field is represented by A-p, where p is the momentum operator. A(r) is the vector potential of the applied electromagnetic field, and is considered to be a classical wave of polarization. This can be seen as \(\hat\epsilon\perp k\) or \(A(r,t)\cong\hat\epsilon A_0e^{ik\cdot r}\). The entire expression is summed over unoccupied final states of energies \(E_f\).
Usually the Golden Rule is reduced to just a one-electron approximation, and calculations are based on the dipole approximation. The dipole approximation assumes that the spatial dependence of the electromagnetic field can be ignored, or \(e^{ik\cdot r}=1\). However, the one-electron final state that should be used is still debated. The final state rule is often implemented in current research. In this approximation, the final state is calculated while considering the screened core-hole. The Hamiltonian used is the final state, one-particle Hamiltonian.
However, for transition metal L2,3 edges (excitation of a 2p electron to a 3d shell), the one-electron approximation is rendered invalid. This is a result of the initial state wave function containing a partially filled d-shell. Upon excitation of a 2p electron to a 3d shell, there are two partially filled shells that have large overlap. Mathematically, this overlap can be written as
\[|\langle\psi_f|A(r)\cdot p|\psi_i\rangle|^2=|\langle\psi_i 2p3d|A(r)\cdot p|\psi_i\rangle|^2 = |\langle\psi_i^*2p^53d^{n+1}|A(r)\cdot p|\psi_i^* 3d^n\rangle|^2 = |\langle 2p^53d^{n+1}|A(r)\cdot p|3d^n\rangle|^2\]
Note that the wave function for the final state is written as \(\psi_i2p3d\).
A little more on the "Interaction Hamiltonian"
The overall interaction Hamiltonian can be written as a sum of the radiation field Hamiltonian, the atomic electron Hamiltonian, and the interaction Hamiltonian.
\[H=H_{RAD}+H_{ATOM}+H_{INT}\]
where the radiation field Hamiltonian, HRAD, can be written
\[H_{RAD}=\sum_{k,\lambda}\hbar\omega_k(n_{k,\lambda}+1/2)\]
where the whole expression is summed over the wave vector, k, and degrees of freedom, \(\lambda\). The term in parenthesis is simply the zero point energy. The kinetic term \(p^2/2m\) and potential energy term \(V(r_i)\) together make up the expression for the Hamiltonian of the atomic electron. The potential energy term considers both the Coulombic interaction with the nucleus, as well as the electron-electron repulsion and spin-orbit interaction.
\[H_{ATOM}=\sum_i\left[\frac{p^2_i}{2m}+V(r_i)\right]\]
Lastly, the interaction Hamiltonian is described as a slight perturbation comprised of two terms. The first of these terms shows the vector field A interacting on the momentum operator p. Another way of stating this is the electron moments being acted on by the electric field E. The second term in the interaction Hamiltonian shows how the magnetic field B, where B=? × A acts on the electron spin ?.
\[H_{INT(l)}=\frac{e}{mc}\sum_i p)i\cdot A(r_i)+\frac{e}{mc}\sum_i\sigma_i\cdot\nabla x A(r_i)\]
So Fermi's Golden Rule gives the transition probability, \(W_{fi}\), between a transition between a system's initial state ( ?i) and final state (?f) upon absorption of a photon of energy \(\hbar\Omega\). This is expressed in the equation
\[W_{fi}=\frac{2\pi}{\hbar}|\langle\phi_f|T|\phi_i\rangle|^2\partial(E_f-E_i-\hbar\Omega)\]
The role of the delta function is to take care of the conservation of energy. A transition occurs if the energy of the final state is equal to the energy of the initial state plus the energy from the x-ray. The transition rate is given by the squared matrix. The Lippman-Schwinger equation gives an expression for the transition operator, T, as
\[T=H_{INT}+H_{INT}\frac{1}{E_i-H+i\Gamma/2}T\]
where H is the Hamiltonian of the unperturbed system, and gamma stands for the excited state's lifetime broadening. In order to describe the one-phone process of x-ray absorption, the equation for T is solved iteratively and in first order where \(T_1 = H_{INT}(1)\). For an electric dipole transition, the transition operator is expressed as
\[T_1=\sum_q e\sqrt{\frac{2\pi\hbar\Omega}{V_5}}e_q\cdot r\]
and for an electric quadrupole transition, the transition operator is described as
\[T_1(EQ)\propto e_{k,\lambda}\cdot Q\cdot\hat k\]
where Q is the quadrupole operator
\[Q=rr-\frac{1}{3}r^2\partial_{ij}\]
Dipole Selection Rules
As stated previously, the dipole transition is able to describe x-ray absorption. When Fermi's golden rule is written in terms of this operator, the probability of a transition, \(W_{fi}\), per unit time is
\[W_{\hbar}=\frac{e^{2}}{\hbar c} \frac{4 \Omega^{3}}{3 c^{2}} n\left|\left\langle\phi_{f}|r| \phi_{i}\right\rangle\right|^{2} \partial\left(E_{f}-E_{i}-h \Omega\right)\]
where the fine structure constant is the first term, \(\frac{e^2}{\hbar c}\). The symbol omega is the excitation frequency and n is the number of photons of the radiation field.The wave functions of an atom can be given quantum numbers J and M, where J is the overall momentum quantum number and M is the magnetic quantum number. If the integral term is written in terms of J and M, the following equation arises, where the radial and angular part of the matrix element can be separated as stated by the Wigner-Eckart theorem.
\[\left\langle\left.\phi_{f}(J M)\right|_{q \lambda} \cdot r | \phi_{i}\left(J^{\prime} M\right)\right\rangle=(-1)^{J-M}\left[\begin{array}{ccc}
J & 1 & J^{\prime} \\
-M & q & M
\end{array}\right]\left\langle\left.\phi_{f}(J)\right|_{q} \cdot r | \phi_{i}\left(J^{\prime}\right)\right\rangle\]
The total momentum quantum number, J, cannot change by more than one unit. Therefore, \(\Delta\)J=+1, 0 or -1. The magnetic quantum number, M, can change depending on the x-ray polarization. This can be stated as \(\Delta\)M=q. The incident x-ray has an angular momentum quantum number l value of lhv=1, and conservation of this angular momentum yields \(\Delta\)l=+1 or -1. The excited electron has an l value different from the original core state by 1. The spin quantum number, s, has the selection rule of \(\Delta\)sj=0, as the x-ray has no associated spin and this must be conserved. When an electron in the 1s core state is excited, the only state that is accessible is the p state. However, from the p state, either the s or d final states are accessible.
The line strength of the transition can be written in terms of the radial part of the previous equation, or as
\[S=e^2\cdot|\langle\phi_f(J)|e_q\cdot r|\phi_i(J^\prime)\rangle|^2\]
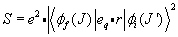 .
.
\[S=e^{2} \cdot\left|\left\langle\phi_{f}(J)\left|e_{q} \cdot r\right| \phi_{i}(J \eta)^{2}\right \rangle\right.\]
Then the transition probability, \(W_{ij}\), can be rewritten to include the \(S\) term.
\[W_{A}=\frac{1}{\hbar c} \frac{4 \Omega^{3}}{3 c^{2}} n\left[\begin{array}{ccc}
J & 1 & J^{\prime} \\
-M & q & M
\end{array}\right]^{2} S \partial\left(E_{f}-E_{i}-h \Omega\right)\]
If the squared-J symbol is assumed to be unity, this can be written as
\[W_{n}=\frac{1}{\hbar c} \frac{4 \Omega^{3}}{3 c^{2}} n S \partial\left(E_{f}-E_{i}-h \Omega\right).\]
Photon flux, the x-ray absorption cross-section, and the oscillator strength
As seen in the previous equation, the transition probability is actually proportional to n, then number of photons, which is directly related to photon flux. The formula for photon flux \(F_p\) can be written as
\[F_{p}=n \frac{\Omega^{2}}{\pi \hbar c^{2}}\]
The x-ray absorption cross section, \(\sigma\), is given in m2 in the following equation, and is directly proportional to the value of f which is the oscillator strength.
\[\begin{aligned} \sigma &= \frac{W_{fi}}{F_p}=\frac{4\pi^2\Omega}{3c}S\partial(E_f=E_i-\hbar\Omega) \\ \sigma &= \frac{2\pi^2e^2}{mc}f \end{aligned}\]
The penetration depth, \(\lambda_{p}\), of the x-rays is directly influenced by the cross section via
\[\lambda_{p}=\dfrac{1}{\rho \sigma}\]
with the term \(\rho\) being the density of the system. Here, the units of cross-section are typically given in values of angstroms-squared. Also, it is common to define the term "inverse density", or the space occupied by one atom of interest, as
\[V_{a t}=1 / \rho\]
and the equation for penetration depth can be re-written as
\[\lambda_{p}=\frac{V_{n t}}{\sigma}\]
Practice Problem
- For La metal, which has a \(V_{at}\) value of cubic angstroms, and a cross section of 0.15 square angstroms, what is the penetration depth?
- What is the difference between XAS and XPS?
- What information does the absorption edge yield?
References
- Liebhafsky, H., et al. X-rays, Electrons, and Analytical Chemistry. John Wiley & Sons. 1972.
- Que, L. Physical Methods in Bioinorganic Chemistry. Sasuolito, California: University Science Books, 2000.
- Skoog, D.; Holler, F.; Nieman, T. Principles of Instrumental Analysis. Fifth ed.; Brooks/Cole: 1998.
- Ankudinov, A.L., Rehr, J.J., "New Developments in the Theory of X-ray Absorption and Core Photoemission." Journal of Electron Spectroscopy and Related Phenonemon. 2001, 114, 1115-1121
- Rehr, J.J., "Theory and Calculations of X-ray Spectra: XAS, XES, XRS, and NRIXS." Radiation Physics and Chemistry. 2006, 75, 1547-1558
- Albers, R.C., Rehr, J.J., "Theoretical Approaches to X-ray Absorption Fine Structure." Reviews of Modern Physics. 2000, 72, 621-654
- De Groot, F., Kotani, A. Core Level Spectroscopy of Solids. CRC Press: 2008.

