How an FTIR Spectrometer Operates
- Page ID
- 1844
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)FTIR spectrometers (Fourier Transform Infrared Spectrometer) are widely used in organic synthesis, polymer science, petrochemical engineering, pharmaceutical industry and food analysis. In addition, since FTIR spectrometers can be hyphenated to chromatography, the mechanism of chemical reactions and the detection of unstable substances can be investigated with such instruments.
Introduction
The range of Infrared region is 12800 ~ 10 cm-1 and can be divided into near-infrared region (12800 ~ 4000 cm-1), mid-infrared region (4000 ~ 200 cm-1) and far-infrared region (50 ~ 1000 cm-1). The discovery of infrared light can be dated back to the 19th century. Since then, scientists have established various ways to utilize infrared light. Infrared absorption spectroscopy is the method which scientists use to determine the structures of molecules with the molecules’ characteristic absorption of infrared radiation. Infrared spectrum is molecular vibrational spectrum. When exposed to infrared radiation, sample molecules selectively absorb radiation of specific wavelengths which causes the change of dipole moment of sample molecules. Consequently, the vibrational energy levels of sample molecules transfer from ground state to excited state. The frequency of the absorption peak is determined by the vibrational energy gap. The number of absorption peaks is related to the number of vibrational freedom of the molecule. The intensity of absorption peaks is related to the change of dipole moment and the possibility of the transition of energy levels. Therefore, by analyzing the infrared spectrum, one can readily obtain abundant structure information of a molecule. Most molecules are infrared active except for several homonuclear diatomic molecules such as O2, N2 and Cl2 due to the zero dipole change in the vibration and rotation of these molecules. What makes infrared absorption spectroscopy even more useful is the fact that it is capable to analyze all gas, liquid and solid samples. The common used region for infrared absorption spectroscopy is 4000 ~ 400 cm-1 because the absorption radiation of most organic compounds and inorganic ions is within this region.
FTIR spectrometers are the third generation infrared spectrometer. FTIR spectrometers have several prominent advantages: (1) The signal-to-noise ratio of spectrum is significantly higher than the previous generation infrared spectrometers. (2) The accuracy of wavenumber is high. The error is within the range of ± 0.01 cm-1. (3) The scan time of all frequencies is short (approximately 1 s). (4) The resolution is extremely high (0.1 ~ 0.005 cm-1). (5) The scan range is wide (1000 ~ 10 cm-1). (6) The interference from stray light is reduced. Due to these advantages, FTIR Spectrometers have replaced dispersive IR spectrometers.
Development of IR Spectrometers
Up till FTIR spectrometers, there have been three generations of IR spectrometers.
- The first generation IR spectrometer was invented in late 1950s. It utilizes prism optical splitting system. The prisms are made of NaCl. The requirement of the sample’s water content and particle size is extremely strict. Further more, the scan range is narrow. Additionally, the repeatability is fairly poor. As a result, the first generation IR spectrometer is no longer in use.
- The second generation IR spectrometer was introduced to the world in 1960s. It utilizes gratings as the monochrometer. The performance of the second generation IR spectrometer is much better compared with IR spectrometers with prism monochrometer, But there are still several prominent weaknesses such as low sensitivity, low scan speed and poor wavelength accuracy which rendered it out of date after the invention of the third generation IR spectrometer.
- The invention of the third generation IR spectrometer, Fourier transform infrared spectrometer, marked the abdication of monochrometer and the prosperity of interferometer. With this replacement, IR spectrometers became exceptionally powerful. Consequently, various applications of IR spectrometer have been realized.
Dispersive IR Spectrometers
To understand the powerfulness and usefulness of FTIR spectrometer, it is essential to have some background information of dispersive IR Spectrometer. The basic components of a dispersive IR spectrometer include a radiation source, monochromator, and detector. The common IR radiation sources are inert solids that are heated electrically to promote thermal emission of radiation in the infrared region of the electromagnetic spectrum. The monochromator is a device used to disperse or separate a broad spectrum of IR radiation into individual narrow IR frequencies.
Generally, dispersive spectrometers have a double-beam design with two equivalent beams from the same source passing through the sample and reference chambers as independent beams. These reference and sample beams are alternately focused on the detector by making use of an optical chopper, such as, a sector mirror. One beam will proceed, traveling through the sample, while the other beam will pass through a reference species for analytical comparison of transmitted photon wavefront information.
After the incident radiation travels through the sample species, the emitted wavefront of radiation is dispersed by a monochromator (gratings and slits) into its component frequencies. A combination of prisms or gratings with variable-slit mechanisms, mirrors, and filters comprise the dispersive system. Narrower slits gives better resolution by distinguishing more closely spaced frequencies of radiation and wider slits allow more light to reach the detector and provide better system sensitivity. The emitted wavefront beam (analog spectral output) hits the detector and generates an electrical signal as a response.
Detectors are devices that convert the analog spectral output into an electrical signal. These electrical signals are further processed by the computer using mathematical algorithm to arrive at the final spectrum. The detectors used in IR spectrometers can be classified as either photon/quantum detectors or thermal detectors.
It is the absorption of IR radiation by the sample, producing a change of IR radiation intensity, which gets detected as an off-null signal (e.g. different from reference signal). This change is translated into the recorder response through the actions of synchronous motors. Each frequency that passes through the sample is measured individually by the detector which consequently slows the process of scanning the entire IR region. A block diagram of a classic dispersive IR spectrometer is shown in Figure \(\PageIndex{1}\).

FTIR Spectrometers
The Components of FTIR Spectrometers
A common FTIR spectrometer consists of a source, interferometer, sample compartment, detector, amplifier, A/D convertor, and a computer. The source generates radiation which passes the sample through the interferometer and reaches the detector. Then the signal is amplified and converted to digital signal by the amplifier and analog-to-digital converter, respectively. Eventually, the signal is transferred to a computer in which Fourier transform is carried out. Figure \(\PageIndex{2}\) is a block diagram of an FTIR spectrometer.
The major difference between an FTIR spectrometer and a dispersive IR spectrometer is the Michelson interferometer.
Michelson Interferometer
The Michelson interferometer, which is the core of FTIR spectrometers, is used to split one beam of light into two so that the paths of the two beams are different. Then the Michelson interferometer recombines the two beams and conducts them into the detector where the difference of the intensity of these two beams are measured as a function of the difference of the paths. Figure \(\PageIndex{3}\) is a schematic of the Michelson Interferometer.
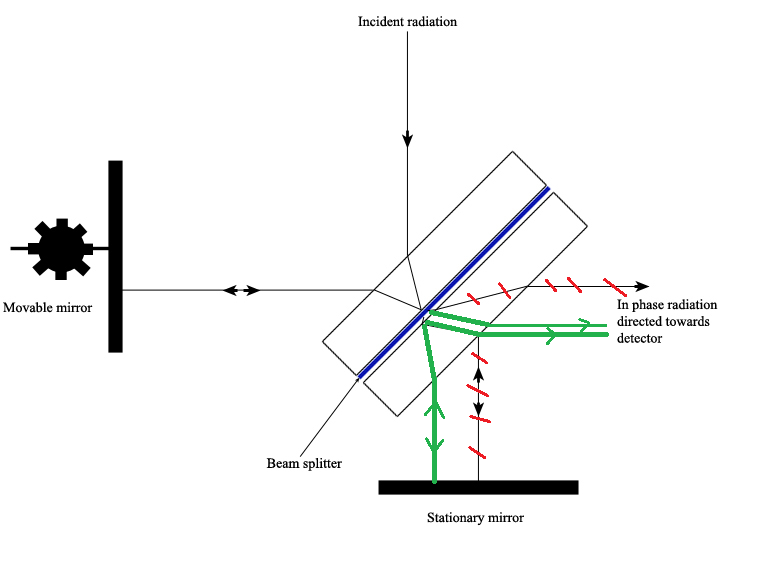
A typical Michelson interferometer consists of two perpendicular mirrors and a beamsplitter. One of the mirror is a stationary mirror and another one is a movable mirror. The beamsplitter is designed to transmit half of the light and reflect half of the light. Subsequently, the transmitted light and the reflected light strike the stationary mirror and the movable mirror, respectively. When reflected back by the mirrors, two beams of light recombine with each other at the beamsplitter.
If the distances travelled by two beams are the same which means the distances between two mirrors and the beamsplitter are the same, the situation is defined as zero path difference (ZPD). But imagine if the movable mirror moves away from the beamsplitter, the light beam which strikes the movable mirror will travel a longer distance than the light beam which strikes the stationary mirror. The distance which the movable mirror is away from the ZPD is defined as the mirror displacement and is represented by ∆. It is obvious that the extra distance travelled by the light which strikes the movable mirror is 2∆. The extra distance is defined as the optical path difference (OPD) and is represented by delta. Therefore,
\[\delta =2\Delta \label{1} \]
It is well established that when OPD is the multiples of the wavelength, constructive interference occurs because crests overlap with crests, troughs with troughs. As a result, a maximum intensity signal is observed by the detector. This situation can be described by the following equation:
\[\delta =n\lambda \label{2} \]
with n = 0,1,2,3...
In contrast, when OPD is the half wavelength or half wavelength add multiples of wavelength, destructive interference occurs because crests overlap with troughs. Consequently, a minimum intensity signal is observed by the detector. This situation can be described by the following equation:
\[\delta =(n+\dfrac{1}{2})\lambda \label{3} \]
with n = 0,1,2,3...
These two situations are two extreme situations. If the OPD is neither n-fold wavelengths nor (n+1/2)-fold wavelengths, the interference should be between constructive and destructive. So the intensity of the signal should be between maximum and minimum. Since the mirror moves back and forth, the intensity of the signal increases and decreases which gives rise to a cosine wave. The plot is defined as an interferogram. When detecting the radiation of a broad band source rather than a single-wavelength source, a peak at ZPD is found in the interferogram. At the other distance scanned, the signal decays quickly since the mirror moves back and forth. Figure \(\PageIndex{4}\)(a) shows an interferogram of a broad band source.
Fourier Transform of Interferogram to Spectrum
The interferogram is a function of time and the values outputted by this function of time are said to make up the time domain. The time domain is Fourier transformed to get a frequency domain, which is deconvolved to product a spectrum. Figure \(\PageIndex{4}\) shows the Fast Fourier transform from an interferogram of polychromatic light to its spectrum.
The Fourier Transform
The first one who found that a spectrum and its interferogram are related via a Fourier transform was Lord Rayleigh. He made the discover in 1892. But the first one who successfully converted an interferogram to its spectrum was Fellgett who made the accomplishment after more than half a century. Fast Fourier transform method on which the modern FTIR spectrometer based was introduced to the world by Cooley and Turkey in 1965. It has been applied widely to analytical methods such as infrared spectrometry, nuclear magnetic resonance and mass spectrometry due to several prominent advantages which are listed in Table \(\PageIndex{1}\).
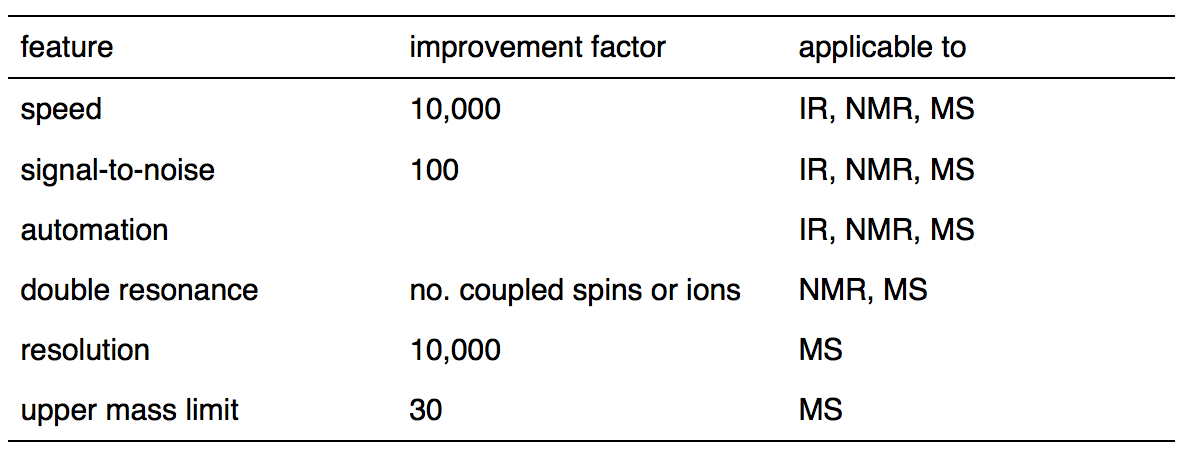
Table \(\PageIndex{1}\). Advantages of Fourier Transform over Continuous-Wave Spectrometry
Fourier transform, named after the French mathematician and physicist Jean Baptiste Joseph Fourier, is a mathematical method to transform a function into a new function. The following equation is a common form of the Fourier transform with unitary normalization constants:
in which t is time, i is the square root of -1.
The following equation is another form of the Fourier transform(cosine transform) which applies to real, even functions:
The following equation shows how f(t) is related to F(v) via a Fourier transform:
An Alternative Explanation of the Fourier Transform in FTIR Spectrometers
The math description of the Fourier transform can be tedious and confusing. An alternative explanation of the Fourier transform in FTIR spectrometers is provided here before we jump into the math description to give you a rough impression which may help you understand the math description.
The interferogram obtained is a plot of the intensity of signal versus OPD. A Fourier transform can be viewed as the inversion of the independent variable of a function. Thus, Fourier transform of the interferogram can be viewed as the inversion of OPD. The unit of OPD is centimeter, so the inversion of OPD has a unit of inverse centimeters, cm-1. Inverse centimeters are also known as wavenumbers. After the Fourier transform, a plot of intensity of signal versus wavenumber is produced. Such a plot is an IR spectrum. Although this explanation is easy to understand, it is not perfectly rigorous.
Simplified Math Description of the Fourier Transform in FTIR
The wave functions of the reflected and transmitted beams may be represented by the general form of:
\[E_{1}=rtc E_{m}\times \cos(\nu t-2\pi kx) \label{7} \]
and
\[E_{1}=rtc E_{m}\times \cos[\nu t-2\pi k(\nu x+\Delta d)] \label{8} \]
where
- \(\Delta{d}\) is the path difference,
- \(r\) is the reflectance (amplitude) of the beam splitter,
- \(t\) is the transmittance, and
- \(c\) is the polarization constant.
The resultant wave function of their superposition at the detector is represented as:
\[E=E_{1}+E_{2}=2(r\times t\times c\times E_{m})\times \cos(\nu t-2\pi kx)\cos(\pi k\Delta d) \label{9} \]
where Em,, ν, and k are the amplitude, frequency and wave number of the IR radiation source.
The intensity (\(I\)) detected is the time average of \(E_2\) and is written as
\[I=4r^{2}t^{2}c^{2}E_{m}^{2}cos^{2}(\nu t-2\pi kx)\cos^{2}(\pi k\Delta d) \label{10} \]
Since the time average of the first cosine term is just ½, then
\[I=2I(k)\cos^{2}(\pi k\Delta d) \label{11} \]
and
\[I(\Delta d)=I(k)[1+\cos(2\pi k\Delta d)]\label{12} \]
where \(I(k)\) is a constant that depends only upon \(k\) and \(I(∆d)\) is the interferogram.
From \(I(∆d)\) we can get \(I(k)\) using Fourier transform as follows:
\[I(\Delta d)-I(\infty)=\int_{0}^{k_{m}}I(k)\cos(2\Pi k\Delta d)dk \label{13} \]
Letting Km →∞, we can write
\[I(k)=\int_{0}^{\infty}[I(\Delta d)-I(\infty)]\cos(2\Pi k\Delta d)d\Delta d \label{14} \]
The physically measured information recorded at the detector produces an interferogram, which provides information about a response change over time within the mirror scan distance. Therefore, the interferogram obtained at the detector is a time domain spectrum. This procedure involves sampling each position, which can take a long time if the signal is small and the number of frequencies being sampled is large.
In terms of ordinary frequency, \(\nu\), the Fourier transform of this is given by (angular frequency \(\omega= s\pi \nu\)):
\[f(\nu )=\int_{-\infty}^{\infty}f(t)e^{-i2\Pi \nu t}dt \label{15} \]
The inverse Fourier transform is given by:
\[f(\nu )=\int_{-\infty}^{\infty}f(t)e^{+i2\pi \nu t}dt \label{16} \]
The interferogram is transformed into IR absorption spectrum (Figure \(\PageIndex{5}\)) that is commonly recognizable with absorption intensity or % transmittance plotted against the wavelength or wavenumber. The ratio of radiant power transmitted by the sample (I) relative to the radiant power of incident light on the sample (I0) results in quantity of Transmittance, (T). Absorbance (A) is the logarithm to the base 10 of the reciprocal of the transmittance (T):
\[A=log_{10}\dfrac{1}{T}=-log_{10}T=-log_{10}\dfrac{I}{I_{0}} \label{17} \]
Hands-on Operation of an FTIR Spectrometer
Step 1: The first step is sample preparation. The standard method to prepare solid sample for FTIR spectrometer is to use KBr. About 2 mg of sample and 200 mg KBr are dried and ground. The particle size should be unified and less than two micrometers. Then, the mixture is squeezed to form transparent pellets which can be measured directly. For liquids with high boiling point or viscous solution, it can be added in between two NaCl pellets. Then the sample is fixed in the cell by skews and measured. For volatile liquid sample, it is dissolved in CS2 or CCl4 to form 10% solution. Then the solution is injected into a liquid cell for measurement. Gas sample needs to be measured in a gas cell with two KBr windows on each side. The gas cell should first be vacuumed. Then the sample can be introduced to the gas cell for measurement.
Step 2: The second step is getting a background spectrum by collecting an interferogram and its subsequent conversion to frequency data by inverse Fourier transform. We obtain the background spectrum because the solvent in which we place our sample will have traces of dissolved gases as well as solvent molecules that contribute information that are not our sample. The background spectrum will contain information about the species of gases and solvent molecules, which may then be subtracted away from our sample spectrum in order to gain information about just the sample. Figure \(\PageIndex{6}\) shows an example of an FTIR background spectrum.
The background spectrum also takes into account several other factors related to the instrument performance, which includes information about the source, interferometer, detector, and the contribution of ambient water (note the two irregular groups of lines at about 3600 cm–1 and about 1600 cm–1 in Figure \(\PageIndex{6}\)) and carbon dioxide (note the doublet at 2360 cm–1 and sharp spike at 667 cm–1 in Figure \(\PageIndex{6}\)) present in the optical bench.
Step 3: Next, we collect a single-beam spectrum of the sample, which will contain absorption bands from the sample as well as the background (gaseous or solvent).
Step 4: The ratio between the single-beam sample spectrum and the single beam background spectrum gives the spectrum of the sample (Figure \(\PageIndex{7}\)).
Step 5: Data analysis is done by assigning the observed absorption frequency bands in the sample spectrum to appropriate normal modes of vibrations in the molecules.
Portable FTIR Spectrometers
Despite of the powerfulness of traditional FTIR spectrometers, they are not suitable for real-time monitoring or field use. So various portable FTIR spectrometers have been developed. Below are two examples.
Ahonen et al developed a portable, real-time FTIR spectrometer as a gas analyzer for industrial hygiene use. The instrument consists of an operational keyboard, a control panel, signal and control processing electronics, an interferometer, a heatable sample cell and a detector. All the components were packed into a cart. To minimize the size of the instrument, the resolution of FTIR spectrometer was sacraficed. But it is good enough for the use of industrial hygiene. The correlation coefficient of hygienic effect between the analyzer and adsorption tubes is about 1 mg/m3.
Korb et al developed a portable FTIR spectrometer which only weighs about 12.5 kg so that it can be held by hand. Moreover, the energy source of the instrument is battery so that the mobility is significantly enhanced. Besides, the instrument can function well within the temperature range of 0 to 45 oC and the humidity range of 0 to 100%. Additionally, this instrument resists vibration. It works well in an operating helicopter. Consequently, this instrument is excellent for the analysis of radiation from the surface and atmosphere of the Earth. The instrument is also very stable. After a three-year operation, it did not lose optical alignment. The reduction of size was implemented by a creative design of optical system and accessory components. Two KBr prisms were used to constitute the interferometer cavity. Optical coatings replaced the mirrors and beam splitter in the interferometer. The optical path is shortened with a much more compact packaging of components. A small, low energy consuming interferometer drive was designed. It is also mass balanced to resist vibration. The common He-Ne tube was replaced by a smaller laser diode.
References
- Science, 21, 1983, 297
- W.D. Perkins, "Fourier Transform-Infrared Spectroscopy”. Part 1. Instrumentation. Topics in Chemical Instrumentation. Ed. Frank A. Settle, Jr. Journal of Chemical Education, 63:1, January 1986: A5-A10.
- D.A. Skoog and J.J. Leary. “Principles of Instrumental Analysis, 4th Ed.”, Harcourt Brace Jovanovich. Philadelphia, PA, 1992. Chapter 12.
- F. Daniels, J.W. Williams, P. Bender, R.A. Alberty, C.D. Cornwell, J. E. Harriman. "Experimental Physical Chemistry, 7th Ed.”, McGraw-Hill, New York, NY, 1970.
- J.W. Cooley and J.W. Turkey, Math. Comp., 1965, 19, 9
- A.G. Marshall, Acc. Chem. Res., 1985, 18, 316
- A. R. Korb, P. Dybwad, W. Wadsworth, J. W. Salisbury, Applied Optics, 1996, 35, 1679
- I. Ahonen, H. Riipinen, A. Roos, Analyst, 1996, 121, 1253
- D. W. Ball, Field Guide to Spectroscopy, SPIE Publication, Bellingham, 2006
- V. Saptari, Fourier-Transform Spectroscopy Instrumentation Engineering, SPIE Publication, Bellingham, 2003
- P. R. Griffiths, J. A. de Haseth, Fourier Transform Infrared Spectrometry, Wiley, New York, 1986
- B. C. Smith, Fundamentals of Fourier Transform Infrared Spectroscopy, CRC press, 1996
- B. Stuart, Modern Infrared Spectroscopy, Wiley, New York, 1996
- A. L. Smith, Applied Infrared Spectroscopy : Fundamentals, Techniques, and Analytical Problem-solving, Wiley, New York, 1979
- P. R. Griffiths, Chemical Infrared Fourier Transform Spectroscopy, Wiley, New York, 1975

