Nuclear Coupling
- Page ID
- 79406
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The second effect within molecules that influences the magnitude of Bo for a particular nucleus is nuclear coupling (we will develop what is known as through bond or scalar coupling). Let’s consider the two hydrogen atoms HA and HB in the compound shown below. The X and Y groups are not hydrogen atoms and produce no magnetic fields. In particular, let’s focus on the effect that HB has on HA. We can think of HA “looking over” at HB and ask ourselves about the magnetic field produced by HB.
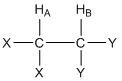
What do you know from earlier in this unit about the magnetic field produced by HB?
Earlier we learned that the nuclear spin of HB results in a magnetic field (BHB) that is aligned either “with” or “against” BAPPL. Furthermore, we learned that essentially 50% of all HB nuclei are aligned “with” and 50% are aligned “against”. So as HA “looks over” at HB, in half the molecules BHB is aligned “with” BAPPL and in the other half of the molecules BHB is aligned “against” BAPPL.
Is the flip of HB’s spin between the “with” and “against” states rapid or slow?
This is an important question, because if the spin flips are rapid, then the effect of HB’s magnetic field on HA would be a time average of the two states, which would average out to zero. Earlier we learned that excited nuclear spin states have relatively long relaxation times. This means that the magnetic field of HB does not rapidly flip back and forth and as HA “looks over”; the field is either “with” or “against” during the time that the measurement is made. Figure 13 shows a representation of the effect of the magnetic field of HB (BHB) on the Bo value of HA with the recognition that the flipping between states is slow in a particular molecule and BHB is either in the “with” or “against” alignment.
The through-bond or scalar coupling is not a through-space effect. Instead, it involves a propagating effect involving the electrons in the intervening s bonds between the two coupled nuclei. Figure 14 shows a representation of the spin of HB and then what preferentially happens with the paired electrons within the three σ bonds that separate HA and HB. Note how the electron spins preferentially align with the spin of HB so that any neighboring set of arrows in the figure are paired up. In the case of HB “with” (top of Figure 14), the closest electron to HA in the σ- bond also has a “with” alignment. In the case of HB “against” (bottom of Figure 14), the closest electron to HA in the σ bond also has an “against” alignment.
What does the resonance for HA look like in the NMR spectrum?
Because the magnetic field of HB has two possible alignments, HA now has two possible Bo values and these are essentially equal in population. Therefore, the resonance consists of two peaks of equal intensity and is called a doublet (see Figure 15). Note, the chemical shift (\(\delta\)) of the doublet shown in Figure 15 would be the value at the exact center of the doublet.
Which peak in the doublet corresponds to BHB “with” and which corresponds to BHB “against”?
Remember that higher energy transitions occur to the left in an NMR spectrum. The peak on the left corresponds to BHB “with” since the Bo value for HA is higher when BHB is “with” BAPPL.
The difference in chemical shift between the two peaks of the doublet is known as the coupling constant. The coupling constant is denoted by J, so the particular coupling constant in Figure 15 would be denoted as JAB.
There are times when it is desirable to decouple a hydrogen atom. In this case, if we were to decouple HB, then the resonance for HA would no longer look like a doublet but would look like a singlet.
Can you think of a way to decouple a hydrogen atom like HB?
We need to consider two prior things we learned in this unit to figure out how to decouple a hydrogen atom. One is that we observe coupling because HB in a particular molecule is aligned either “with” or “against” the applied field as the measurement of HA is being recorded. So, if there were some way to have HB rapidly exchange back and forth between its “with” or “against” states, the net magnetic field would average to zero and the coupling would go away. The second is to remember what happens when a resonance is saturated and has equal populations of the ground and excited states. In this case, incident photons either promote ground state nuclei to the excited state or cause excited state nuclei to undergo stimulated emission and go back to the ground state. Both of these processes involve exchanges of nuclei between the two states.
So the way to decouple HB is to put in a high power RF at the frequency needed to excite HB. This high power RF will saturate the transition of HB and promote rapid exchange of HB nuclei back and forth between the two states either through absorption or stimulated emission. This rapid exchange causes the magnetic field that HA experiences from HB to average out to zero.
What would the HB resonance look like?
The same type of arguments hold as HB “looks over” at HA: 50% of the molecules have BHA aligned “with” and 50% have BHA aligned “against”. Therefore HB will also be a doublet. Also, there is only a single magnitude of coupling between two nuclei so the split between the two peaks of the doublet for HB is exactly identical to that of HA.
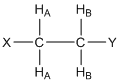
What would the resonance for HA look like in the compound shown below where there are two HB protons? Provide a rationale for your answer.

First, it is important to recognize that the two HB protons are chemically equivalent because there is rapid rotation about the C-C bond. Second, each of the HB protons has a 50:50 chance of having its magnetic field aligned “with” (W) or “against” (A) the applied magnetic field. This leads to four possibilities of the alignment of the magnetic fields of the HB protons, each of which has an equal probability of occurrence: WW(↑↑)/WA(↑↓)/AW(↓↑)/AA(↓↓). Note that for the center two (WA/AW), the two magnetic fields cancel each other out and, overall, there is twice the probability of this situation. The resulting resonance looks like that in Figure 16 and is said to be a 1:2:1 triplet. Note, the chemical shift (\(\delta\)) of the triplet shown in Figure 16 would be the value for the center peak.
The coupling constant JAB would be the distance between one of the outer peaks and the center peak as shown in Figure 16. To convince yourself that this is correct, you could also think of this as a situation where one of the HB protons couples to HA and splits it into a doublet. Then the second HB couples to HA and splits each of the two peaks into a doublet as shown in Figure 17. Since the middle ones overlap, the intensity of the center peak of the triplet is twice that of the two outer peaks.
Which peak of the triplet corresponds to the WW and which to the AA situation?
The WW situation causes the largest value of Bo, the largest energy gap, and highest frequency of excitation. Therefore it is furthest to the left as shown in Figure 16.
The shape of a resonance split by any number of equivalent hydrogen atoms can be conveniently determined using what is known as Pascal’s triangle (Figure 18). To complete Pascal’s triangle, the number 1 is always put on the outside and the inner numbers are obtained by adding together the two adjoining numbers in the row above. So coupling to no hydrogens causes a singlet; coupling to one causes a 1:1 doublet; coupling to two causes a 1:2:1 triplet; coupling to three causes a 1:3:3:1 quartet, etc.
\(\begin{alignat}{3}
\ce{&1 &&No\: coupling\\\
1 & : 1 &&One\: hydrogen\: couples\\
1:\:\: &2:1 &&Two\: hydrogens\: couple\\
1:3&:3:1 &&Three\: hydrogens\: couple\\
1:4:\:\: &6:4:1 &&Four\: hydrogens\: couple\\
1:5:10&:10:5:1 \quad\quad &&Five\: hydrogens\: couple}
\end{alignat}\)
Figure 18. Pascal’s triangle showing the number and relative areas of the peaks of a resonance for different number of coupling hydrogen atoms. Note, the coupling hydrogen atoms must be chemically equivalent to apply these rules.
What factors do you think influence the magnitude of the coupling constant?
The magnitude of a coupling constant depends on two factors. One is the distance between the two nuclei that are coupled. Generally the further apart the two nuclei the smaller the magnitude of the coupling. The second is that the coupling constant has an angular dependence. For the examples we have considered above, HA and HB are three bonds removed from each other. These nuclei have what is known as a dihedral angle that can be determined using a Newman projection as shown in Figure 19. In this case, since there would likely be rapid rotation about the C-C bond, the dihedral angle would be a time-averaged value.
If the geometry was locked in place, as is common with rigid bicyclic organic compounds, then the Karplus correlation that is shown in Figure 20 relates the magnitude of the coupling constant to the dihedral angle. Note that there is quite an angular dependence to the coupling constant with the largest 3-bond coupling (also called vicinal coupling) occurring for two nuclei with a dihedral angle of 180o (J \(\simeq\) 13 Hz) and the smallest occurring at a dihedral angle of about 85o (J \(\simeq\) 2 Hz). There is also an angular Karplus correlation relationship for 2-bond coupling (also called geminal coupling) that is shown in Figure 21. It is important to note that the coupling constants predicted by the angular relationships shown in Figures 20 and 21 are approximations. Other facets of the compound being studied have an influence on the exact coupling constant.
Predict the coupling constants that would occur between HA, HM and HX and the mono-substituted alkene shown below and draw the shape of each resonance.
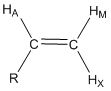
The AMX designation for hydrogen atoms is known as the Pople notation. The use of AMX indicates that the three hydrogen resonances have distinctly different chemical shifts. An ABC notation would indicate close and overlapping resonance.
The first thing to recognize is that all three of these protons are chemically different. HA has 3-bond coupling to HM (dihedral angle of 0o, JAM \(\simeq\) 11 Hz) and 3-bond coupling to HX (dihedral angle of 180o, JAX \(\simeq\) 13 Hz). HA would be described as a doublet of doublets and the shape of the resonance is shown in Figure 22. HM has 3-bond coupling to HA (dihedral angle of 0o, JAM \(\simeq\) 11 Hz) and 2-bond coupling to HX (angle of 120o, JMX \(\simeq\) 3 Hz). HM would be described as a doublet of doublets and the shape of the resonance is shown in Figure 20. HX has 3-bond coupling to HA (dihedral angle of 180o, JAM \(\simeq\) 13 Hz) and 2-bond coupling to HM (angle of 120o, JMX \(\simeq\) 3 Hz). HX would be described as a doublet of doublets and the shape of the resonance is shown in Figure 22. There are two interesting observations for the alkene resonances. First, all three are distinctly different because of the different magnitudes of the coupling constants such that all could be readily assigned in an NMR spectrum. Figure 22 also shows the distance in Hz between the two extreme peaks of each resonance for HA (24 Hz), HM (14 Hz) and HX (16 Hz). Second, the geminal or 2-bond HM-HX coupling is smaller than the vicinal or 3-bond HA-HM and HA-HX coupling when the angle terms are considered. The example for a mono-substituted alkene provides a glimpse into the valuable information about molecular structure that can be gained by examining whether coupling occurs and the magnitude of coupling between different nuclei of a molecule.
An especially important observation is that the magnitude of coupling constants does not depend on BAPPL. One reason is that the distance and angle between two nuclei are independent of BAPPL. Another is that the magnetic field generated by a spinning proton is dependent on its magnetic moment and spin properties, and neither of these is dependent on BAPPL. The fact that coupling constants are independent of BAPPL has especially important consequences in NMR spectroscopy.
Consider the following compound in which JAB = 10 Hz, \(\delta\)HA = 1.3 ppm and \(\delta\)HB = 1.2 ppm. Draw the resulting spectrum if the spectrum is recorded on a 100 MHz and 400 MHz spectrometer.
Both resonances will be 1:2:1 triplets and the outer peaks of both triplets are each 10 Hz removed from the center peak. The important distinction is that the 100 MHz instrument has 100 Hz in a ppm whereas the 400 MHz instrument has 400 Hz in a ppm. Figure 23 shows representations for the two different instruments. What is important to note is that the two resonances (one in black, one in red) will overlap on the 100 MHz instrument (Figure 23a), whereas on the 400 MHz instrument they are well separated from each other (Figure 23b). In order words, the 400 MHz instrument has much better resolution or dispersion than the 100 MHz instrument. When the difference in chemical shift between coupled hydrogen atoms is greater than their coupling constant, the spectrum is said to be first order. First order spectra are readily interpreted according to the established rules for coupling. When the coupling constant is equal to or larger than the difference in chemical shift between the coupled hydrogen atoms, the spectrum is second order and interpretation is more difficult. Because NMR spectrometers with higher field strengths have more Hertz in a ppm, the spectra are more likely to be first order. We already discussed how higher field strengths increase the sensitivity because of the more favorable population distribution between the ground and excited states. Another reason why many people want higher field spectrometers is because of the improvement in resolution over lower field instruments. The need for higher resolution is especially important for complex molecules such as many natural products and proteins.
One last thing to examine is the actual shape of the resonance for the example above that would appear in the spectrum recorded on a 100 MHz instrument. In Figure 23a, the resonance appears to look like a 1:3:3:1 quartet. In fact, the resonance would not look like that but would show an additional distortion that might further complicate interpretation of the spectrum. The distortion results because coupled systems are no longer independent of each other and the coupled nuclei may distort the populations of their different energy levels. The degree of distortion depends on the magnitude of the difference in their chemical shifts relative to the magnitude of the difference in their coupling constants. If the two coupled resonances are well separated in the spectrum, minimal to no distortion occurs. If they are close together, much greater distortion occurs.
An example of this distortion is most easily illustrated for two protons that split each other into doublets. In Figure 24, the two doublets have a coupling constant of 10 Hz and the different spectra correspond to frequencies of absorption that decrease by 10 Hz each going from Figure 24a to 24e. In Figure 24a, the two resonances have the largest difference in chemical shifts and both peaks look almost like regular doublets. As the chemical shifts become closer (Figure 24b-e), note the increasing distortion that occurs. This is often referred to as “leaning”; resonances “lean” toward other resonances they are coupled to. Remember, the equal intensity of both peaks in a doublet occurred because of the 50:50 probability of the “with” and “against” alignment, so the distortion represents an alteration of these populations within the coupled system. In some of the spectra (Figure 24a-b), the leaning is relatively mild such that one might recognize that it involves two coupled doublets. However, when the chemical shifts get very close (Figure 24d-e), the distortion is so great that interpretation is more difficult. For example, the spectrum in Figure 24d might easily get confused as a 1:3:3:1 quartet. If two coupled protons have identical chemical shifts, then no coupling is observed in the spectrum and the peaks would appear as a singlet.


