Hyperfine Splitting
- Page ID
- 1795
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)This splitting occurs due to hyperfine coupling (the EPR analogy to NMR’s J coupling) and further splits the fine structure (occurring from spin-orbit interaction and relativistic effects) of the spectra of atoms with unpaired electrons. Although hyperfine splitting applies to multiple spectroscopy techniques such as NMR, this splitting is essential and most relevant in the utilization of electron paramagnetic resonance (EPR) spectroscopy.
Introduction
Hyperfine Splitting is utilized in EPR spectroscopy to provide information about a molecule, most often radicals. The number and identity of nuclei can be determined, as well as the distance of a nucleus from the unpaired electron in the molecule. Hyperfine coupling is caused by the interaction between the magnetic moments arising from the spins of both the nucleus and electrons in atoms. As shown in Figure \(\PageIndex{1}\), in a single electron system the electron with its own magnetic moment moves within the magnetic dipole field of the nucleus.
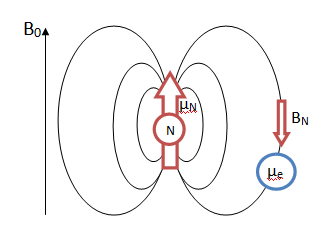
This spin interaction in turn causes splitting of the fine structure of spectral lines into smaller components called hyperfine structure. Hyperfine structure is approximately 1000 times smaller than fine structure. Figure \(\PageIndex{2}\) shows a comparison of fine structure with hyperfine structure splitting for hydrogen, though this is not to scale.
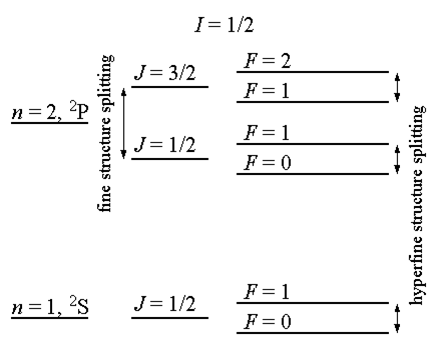
The total angular momentum of the atom is represented by F with regards to hyperfine structure. This is found simply through the relation F=J+I where I is the ground state quantum number and J refers to the energy levels of the system.
Results of Nuclear-Electron Interactions
These hyperfine interactions between dipoles are especially relevant in EPR. The spectra of EPR are derived from a change in the spin state of an electron. Without the additional energy levels arising from the interaction of the nuclear and electron magnetic moments, only one line would be observed for single electron spin systems. This process is known as hyperfine splitting (hyperfine coupling) and may be thought of as a Zeeman effect occurring due to the magnetic dipole moment of the nucleus inducing a magnetic field.
The coupling patterns due to hyperfine splitting are identical to that of NMR. The number of peaks resulting from hyperfine splitting of radicals may be predicted by the following equations where Mi is the number of equivalent nuclei:
- \( \text{# of peaks}=M_{i}I+1 \) for atoms having one equivalent nuclei
- \( \text{# of peaks}=(2M_{1}I_{1}+1)(2M_{2}I_{2}+1).... \) for atoms with multiple equivalent nuclei
For example, in the case of a methyl radical 4 lines would be observed in the EPR spectra. A methyl radical has 3 equivalent protons interacting with the unpaired electron, each with I=1/2 as their nuclear state yielding 4 peaks.
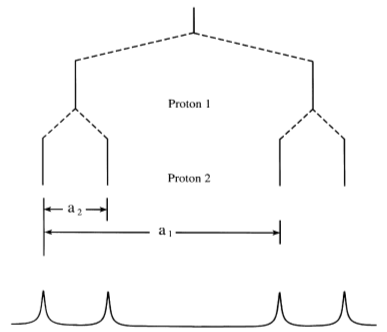
The relative intensities of certain radicals can also be predicted. When I = 1/2 as in the case for 1H, 19F, and 31P, then the intensity of the lines produced follow Pascal's triangle. Using the methyl radical example, the 4 peaks would have relative intensities of 1:3:3:1. The following figures2 show the different splitting that results from interaction between equivalent versus nonequivalent protons.
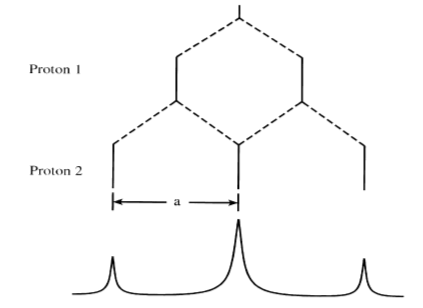
It is important to note that the spacing between peaks is 'a', the hyperfine coupling constant. This constant is equivalent for both protons in the equivalent system but unequal for the unequivalent protons.
The Hyperfine Coupling Constant
The hyperfine coupling constant (\(a\)) is directly related to the distance between peaks in a spectrum and its magnitude indicates the extent of delocalization of the unpaired electron over the molecule. This constant may also be calculated. The following equation shows the total energy related to electron transitions in EPR.
\[ \Delta E=g_e \mu _e M_s B + \sum_i g_{N_i} \mu_{N_i}M_{I_i}(1-\sigma _{i})+\sum_{i}a_i M_s M_{I_i} \]
The first two terms correspond to the Zeeman energy of the electron and the nucleus of the system, respectively. The third term is the hyperfine coupling between the electron and nucleus where \(a_i\) is the hyperfine coupling constant. Figure \(\PageIndex{5}\) shows splitting between energy levels and their dependence on magnetic field strength. In this figure, there are two resonances where frequency equals energy level splitting at magnetic field strengths of \(B_1\) and \(B_2\).
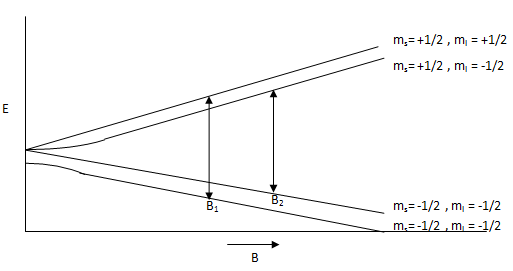
These parameters are essential in the derivation of the hyperfine coupling constant. By manipulating the total energy equation (those interested in the entire derivation, refer to the first outside link), the following two relations may be derived.
\[ B_1= \dfrac {h\nu -a/2} {g\mu_e} \]
\[ B_2= \dfrac{h\nu +a/2}{g\mu_e} \]
From this, the hyperfine coupling constant (\(a\)) may be derived where \(g\) is the g-factor.
\[\begin{align} \Delta B &=B_{2}-B_{1} \\[4pt] &=\dfrac {h\nu +a/2} {g\mu_{e}}- \dfrac {h\nu -a/2}{g\mu_{e}} \end{align}\]
so solving for hyperfine coupling constant results in the following relationship:
\[ a= g\mu_e \Delta B \]
Isotropic and Anisotropic Interactions
Electron-nuclei interactions have several mechanisms, the most prevalent being Fermi contact interaction and dipole interaction. Dipole interactions occur between the magnetic moments of the nucleus and electron as an electron moves around a nucleus. However, as an electron approaches a nucleus, it has a magnetic moment associated with it. As this magnetic moment moves very close to the nucleus, the magnetic field associated with that nucleus is no longer entirely dipolar. The resulting interaction of these magnetic moments while the electron and nucleus are in contact is radically different from the dipolar interaction of the electron when it is outside the nucleus. This non-dipolar interaction of a nucleus and electron spin in contact is the Fermi contact interaction. A comparison of this is shown in Figure \(\PageIndex{6}\). The sum of these interactions is the overall hyperfine coupling of the system.
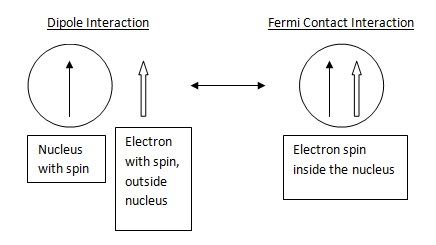
Fermi contact interactions predominate with isotropic interactions, meaning sample orientation to the magnetic field does not affect the interaction. Due to the fact that this interaction only occurs when the electron is inside the nucleus, only electrons in the s orbital exhibit this kind of interaction. All other orbitals (p,d,f) contain a node at the nucleus and can never have an electron at that node. The hyperfine coupling constant in isotropic interactions is denoted 'a'.
Dipole interactions predominate with anisotropic interactions, meaning sample orientation does change the interaction. These interactions depend on the distance between the electron and nuclei as well as the orbital shape. The typical scheme is shown in Figure \(\PageIndex{7}\).
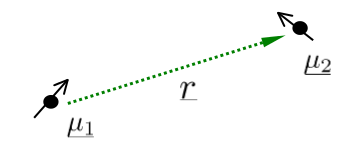
Dipole interactions can allow for positioning paramagnetic species in solid lattices. The hyperfine coupling constant in isotropic interactions is denoted 'B'.
Further splitting may occur by the unpaired electron if the electron is subject to the influence of multiple sets of equivalent nuclei. This splitting is on the order of 2nI+1 and is known as superhyperfine splitting. As hyperfine structure splits fine structure into smaller components, superhyperfine structure further splits hyperfine structure. As a result, these interactions are extremely small but are useful as they can be used as direct evidence for covalency. The more covalent character a molecule exhibits, the more apparent its hyperfine splitting.
For example, in a CH2OH radical, an EPR spectrum would show a triplet of doublets. The triplet would arise from the three protons, but superhyperfine splitting would cause these to split futher into doublets. This is due to the unpaired electron moving to the different nuclei but spending a different length of time on each equivalent proton. In the methanol radical example, the electron lingers the most on the CH2 protons but does move occasionally to the OH proton.
References
- Bunce, N. "Introduction to the interpretation of electron spin resonance spectra of organic radicals." J. Chem. Educ., 1987, 64 (11), p 907
- Griffiths, D. "Hyperfine Splitting in the ground state of Hydrogen." Am. J. Phys., 1982, 50 (8), p 698
- Gasiorowicz, Stephen. Quantum Physics. New York: Wiley, 1974.2
Problems
- What is the number of peaks of a benzene radical in EPR due to hyperfine coupling and what are their relative intensities?
- What is the number of peaks for CH2(OCH3), a methoxymethyl radical in EPR due to hyperfine coupling?
- Why are s orbitals only considered in Fermi contact interactions?
Answers:
- 7 lines, 1:6:15:20:15:6:1 (benzene has 6 equivalent protons so the number of peaks is M+1 = (6+1) = 7 peaks, intensities come from pascal's triangle)
- 12 lines (has two different equivalent nuclei, one with two protons and one with 3 so (M1+1)(M2+1) = (2+1)(3+1) = 12 peaks)
- p, d, and f orbitals have nodes at the nucleus and do not exhibit Fermi contact interactions
Contributors and Attributions
- Stephanie Gray

