8.51: Analysis of the Stern-Gerlach Experiment

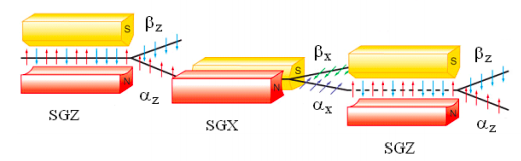
As will be demonstrated in this tutorial, the Stern-Gerlach experiment illustrates several key quantum concepts. The figure shown below is taken from Thomas Engel's text, Quantum Chemistry & Spectroscopy. The figure depicts the behavior of a beam of Na atoms as it interacts with a sequence of three Stern-Gerlach magnets.

We begin with a review of the quantum mechanics of electron spin.

Spin Eigenstates

Spin-up in the z-direction:

\[ \sigma_z = \begin{pmatrix} 1 \\ 0 \end{pmatrix} \nonumber \]

Spin-down in the z-direction:

\[ \beta_z = \begin{pmatrix} 0 \\ 1 \end{pmatrix} \nonumber \]

Spin-up in the x-direction:

\[ \sigma_x = \frac{1}{ \sqrt{2}} \begin{pmatrix} 1 \\ 1 \end{pmatrix} \nonumber \]

Spin-down in the x-direction:

\[ \beta_x = \frac{1}{ \sqrt{2}} \begin{pmatrix} 1 \\ -1 \end{pmatrix} \nonumber \]

Operators

The matrix operators associated with the two Stern-Gerlach magnets are shown below.

SGZ operator:

\[ \text{SGZ} = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} \nonumber \]

SGX operator:

\[ \text{SGX} = \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} \nonumber \]

The α_z and β_z spin states are eigenfunctions of the SGZ operator with eigenvalues +1 and -1, respectively:

\[ \begin{matrix} \text{SGZ} \sigma_z = \begin{pmatrix} 1 \\ 0 \end{pmatrix} & \sigma_z^T \text{SGZ} \alpha_z^T = 1 & \text{SGZ} \beta_z = \begin{pmatrix} 0 \\ -1 \end{pmatrix} & \beta_z^T \text{SGZ} \beta_z = -1 \end{matrix} \nonumber \]

The α_x and β_x spin states are eigenfunctions of the SGX operator with eigenvalues +1 and -1, respectively:

\[ \begin{matrix} \text{SGX} \sigma_x = \begin{pmatrix} 0.707 \\ 0.707 \end{pmatrix} & \sigma_x^T \text{SGX} \alpha_x^T = 1 & \text{SGZ} \beta_x = \begin{pmatrix} -0.707 \\ 0.707 \end{pmatrix} & \beta_z^T \text{SGX} \beta_x = -1 \end{matrix} \nonumber \]

Analysis

Silver atoms are deflected by an inhomogeneous magnetic field because of the two-valued magnetic moment associated with their unpaired 5s electron ([Kr]5s¹4d¹⁰). The beam of silver atoms entering the Stern-Gerlach magnet oriented in the z-direction (SGZ) on the left is unpolarized. This means it is a mixture of randomly spin-polarized Ag atoms. As such, it is impossible to write a quantum mechanical wave function for this initial state. The density operator (or matrix), which is a more general quantum mechanical construct, can be used to represent both pure states and mixtures, as shown below.

\[ \begin{matrix} \hat{ \rho} = | \Psi \rangle \langle \Psi | & \hat{ \rho} = \sum p)i | \Psi_i \rangle \langle \Psi_i | \end{matrix} \nonumber \]

In the equation on the right, pi is the fraction of the mixture in the state Ψ_i. The expectation value for a measurement on a pure or mixed state is written as follows in terms of the appropriate density operator.

\[ \langle A \rangle = Trace ( \hat{ \rho} \hat{A} ) \nonumber \]

An unpolarized beam can be written as a 50-50 mixture of any of the orthogonal spin eigenstates - α_z and β_z, or α_x and β_x, or α_y and β_y. The density operator for the unpolarized spin beam entering the first SGZ is calculated using α_z and β_z.

\[ \rho_{mix} = \frac{1}{2} \begin{pmatrix} 1 \\ 0 \end{pmatrix} \begin{pmatrix} 1 & 0 \end{pmatrix} + \frac{1}{2} \begin{pmatrix} 0 \\ 1 \end{pmatrix} \begin{pmatrix} 0 & 1 \end{pmatrix} = \begin{pmatrix} 0.5 & 0 \\ 0 & 0.5 \end{pmatrix} \nonumber \]

The expectation value for passage through the SGZ magnet is 0, indicating equal amounts of Ag atoms in the spin-up and spin-down exit channels.

\[ \text{tr}( \rho_{mix} \text{SGZ}) = 0 \nonumber \]

The α_z beam emerging from SGZ is directed to the SGX magnet and the αx beam emerging from it is directed to another SGZ magnet. Before the second SGZ it might be assumed that the Ag atoms in the beam are in the electronic spin state |α_z>|α_x>, in other words after the SGZ and SGX magnets the Ag 5s electrons have well-defined values for spin in both the z- and x-directions. The vector representing this state is written in tensor format.

\[ \begin{matrix} I = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} & \Psi^T \text{kronecker(SGZ, I)} \Psi = 1 & \text{kronecker(SGZ, I)} \Psi = \begin{pmatrix} 0.707 \\ 0.707 \\ 0 \\ 0 \end{pmatrix} \end{matrix} \nonumber \]

However, the actual experiment illustrated above shows that the expectation value is 0, with equal numbers of silver atoms emerging in α_z and β_z channels.

The correct quantum mechanical interpretation is that the SGZ and SGX operators do not commute, meaning that they cannot have simultaneous eigenstates.

\[ \text{SGX SGZ} - \text{SGZ SGX} = \begin{pmatrix} 0 & -2 \\ 2 & 0 \end{pmatrix} \nonumber \]

The Ag spin state entering the second SGZ magnet is α_x, an eigenstate of the SGX operator, not simultaneously an eigenstate of SGZ and SGX. It can be written as a superposition of α_z and β_z.

\[ \begin{matrix} \alpha_x = \frac{1}{ \sqrt{2}} ( \alpha_z + \beta_z) & \frac{1}{ \sqrt{2}} \left[ \begin{pmatrix} 1 \\ 0 \end{pmatrix} + \begin{pmatrix} 0 \\ 1 \end{pmatrix} \right] = \begin{pmatrix} 0.707 \\ 0.707 \end{pmatrix} \end{matrix} \nonumber \]

Quantu theory predicts that the exit channels of the second SGZ magnet will be equally populated with Ag atoms.