Skip to main content
Chemistry LibreTexts

11.11: Let's Teach High School Students Computer Algebra Methods

  1. Last updated
  2. Save as PDF
  • Page ID
    135020

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    The algebra problem shown below appears in my grandson's 9th grade math text. He is asked to solve for x and y using the "guess and check" method. It is early in the semester so I do not object, figuring he will be taught more reliable standard methods soon. The method I strongly recommend is to stress that if you have two unknowns, you need two equations, and that those equations should be stated explicitly up front. After that some standard method should be used to find the solution or solutions, by hand or using a calculator or a computer. In this case there are two solutions.

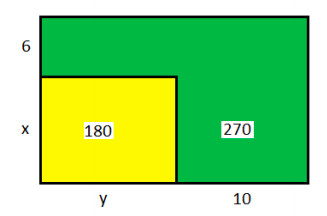
    Screen Shot 2019-01-30 at 1.18.15 PM.png

    In what follows two computer algebra methods using Mathcad are presented. The total area (yellow plus green) is 450, so my two equations are given below. This is the most important part in solving the problem - setting it up and it is what should be stressed in math education. Let the computer or calculator do the tedious stuff. The Mathcad syntax for the first method is as follows:

    \(\begin{bmatrix}
    (x+6) \cdot (y + 10) = 450\\
    x \cdot y = 180
    \end{bmatrix}\) solve, (x, y) \(\rightarrow\begin{pmatrix}
    12 & 15\\
    9 & 20
    \end{pmatrix}\)

    The second method involves eliminating y in the first equation by substitution using the second equation, solving for x and then using the second equation to get the appropriate values for y.

    x := (x + 6) \(\cdot\) (y + 10) = 450 substitute, y = \(\frac{180}{x} \rightarrow \frac{10 \cdot (x+6) \cdot (x+18)}{x} = 450\) solve, x \(\rightarrow \begin{pmatrix}
    9\\
    12
    \end{pmatrix}\)

    Write y in terms of x: y := \(\frac{180}{x}\) Display y values: y = \(\begin{pmatrix}
    20\\
    15
    \end{pmatrix}\)

    High school students are facile in using the computer for word processing, and the internet for resourcing term papers and social networking purposes. It's time they were taught how to use the computer to solve math and science problems.

    Solution templates can be provided to the students so that they can concentrate on setting up the problem, rather than the programming syntax.

    Template for first method: \(\begin{pmatrix}
    \square = \blacksquare\\
    \blacksquare = \blacksquare
    \end{pmatrix}\) solve, \(\begin{pmatrix}
    \blacksquare & \blacksquare
    \end{pmatrix} \rightarrow\)

    Template for second method: ■ := ■ = ■ substitute, ■ = ■ \(\rightarrow\) solve, ■ \(\rightarrow\)

    This page titled 11.11: Let's Teach High School Students Computer Algebra Methods is shared under a CC BY 4.0 license and was authored, remixed, and/or curated by Frank Rioux via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.