10.13: Variation Method for a Particle in a Box with an Internal Barrier

Last updated
Save as PDF

Page ID: 136125

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

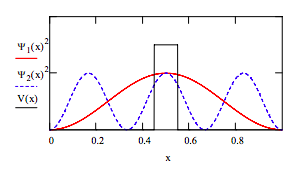
\( \psi _{1} (x) = \sqrt{2} \sin{ \pi x}\)

\( \psi _{2} (x) = \sqrt{2} \sin{3 \pi x}\)

\( V(x) = if [(x \geq .45) (x \leq .55), 3,0]\)

Plot trial wavefunctions and potential energy.

Screen Shot 2019-02-11 at 1.55.32 PM.png

Evaluate matrix elements for \(100 E_h\) internal barrier:

\( S_{11} = \int_{0}^{1} \psi _{1} (x)^{2} dx\) \( S_{11} = 1\)

\( S_{12} = \int_{0}^{1} \psi _{1} (x) \psi _{2} (x) dx\) \( S_{12} = 0\)

\( S_{22} = \int_{0}^{1} \psi _{2} (x)^{2} dx\) \( S_{22} = 1\)

\[ \begin{align} H_{11} &= \int_{0}^{1} \psi _{1} (x) (- \dfrac{1}{2}) \dfrac{d^{2}}{dx^{2}} \psi _{1} (x) dx + \int_{.45}^{.55} \psi _{1} (x)~100~ \psi _{1} (x) dx\\[4pt] & \approx 24.7711\end{align} \nonumber \]

\[\begin{align} H_{12} &= \int_{0}^{1} \psi _{1} (x) (- \dfrac{1}{2}) \dfrac{d^{2}}{dx^{2}} \psi _{2} (x) dx + \int_{.45}^{.55} \psi _{1} (x)~100~ \psi _{2} (x) dx \\[4pt] & \approx -19.1912\end{align} \nonumber \]

\[\begin{align} H_{22} &= \int_{0}^{1} \psi _{2} (x) (- \dfrac{1}{2}) \dfrac{d^{2}}{dx^{2}} \psi _{2} (x) dx + \int_{.45}^{.55} \psi _{2} (x)~100~ \psi _{2} (x) dx \\[4pt] &\approx 62.9972 \end{align} \nonumber \]

Solve the secular equations and normalization constraint for the energy and coefficients.

Seed values for energy and coefficient: E = 5 c₁ = .5 c₂ = .5

Given

\( (H_{11} - E S_{11})c_{1} + (H_{12} - E S_{12})c_{2} = 0\)

\( (H_{12} - E S_{12})c_{1} + (H_{22} - E S_{22})c_{2} = 0\)

\( c_{1}^{2} S_{11} + 2 c_{1} c_{2} S_{12} + c_{2}^{2} S_{22} = 1\)

\({\begin{pmatrix}
E \\
c_{1} \\
c_{2}
\end{pmatrix}} = Find(E, c_{1}, c_{2})\)

\({\begin{pmatrix}
E \\
c_{1} \\
c_{2}
\end{pmatrix}} = {\begin{pmatrix} 16.7989 \\
0.9235\\
0.3836
\end{pmatrix}}\)

Plot variational results:

\( \Phi (x) = c_{1} \Phi _{1} (x) + c_{2} \psi_{2} (x)\)

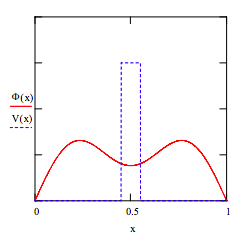
Screen Shot 2019-02-11 at 2.02.23 PM.png

Calculate the probability the particle is in the barrier:

\( \int_{0.45}^{0.55} \Phi (x)^{2} dx = 0.0605\)

Calculate potential and kinetic energy:

\( V = 100 \int_{0.45}^{0.55} \Phi (x)^{2} dx\) \( V = 6.0541\)

\( T = E - V\)

\( T = 10.7448\)