10.9: Momentum-Space Variation Method for the Quartic Oscillator
- Page ID
- 136121
For unit mass the quartic oscillator has the following energy operator in atomic units in coordinate space.
\[ H = - \frac{1}{2} \frac{d^{2}}{dx^{2}} \nonumber \]
Suggested trial wavefunction:
\[ \psi (x, \beta ) = ( \frac{2 \beta}{ \pi})^{ \frac{1}{4}} exp( - \beta x^{2}) \nonumber \]
Demonstrate that the wavefunction is normalized.
\[ \int_{- \infty}^{ \infty} \psi (x, \beta )^{2} dx~assume, \beta >0 \rightarrow 1 \nonumber \]
Fourier transform the coordinate wavefunction into the momentum representation.
\[ \Phi (p, \beta ) = \frac{1}{ \sqrt{2 \pi}} \int_{- \infty}^{ \infty} exp (-i p x) \psi (x, \beta ) dx |_{simplify}^{assume,~ \beta > 1} \rightarrow \frac{1}{2} \frac{2^{ \frac{3}{4}}}{ \pi ^{ \frac{1}{4}}} \frac{ e^{ \frac{-1}{4} \frac{p^{2}}{ \beta}}}{ \beta ^{ \frac{1}{4}}} \nonumber \]
Demonstrate that the momentum wavefunction is normalized.
\[ \int_{- \infty}^{ \infty} \overline{ \Phi (p, \beta )} \Phi (p, \beta ) dp assume,~ \beta > 0 \rightarrow 1 \nonumber \]
The quartic oscillator energy operator in momentum space:
\[ H = \frac{p^{2}}{2} \blacksquare + \frac{d^{4}}{dp^{4}} \blacksquare \nonumber \]
Evaluate the variational energy integral.
\[ E ( \beta ) = \int_{- \infty}^{ \infty} \overline{ \Phi(p, \beta )} \frac{p^2}{2} \Phi (p, \beta ) dp + \int_{- \infty}^{ \infty} \overline{ \Phi (p, \beta )} \frac{d^{4}}{dp^4} \Phi (p, \beta ) dp |_{simplify}^{assume,~ \beta > 0} \rightarrow \frac{1}{16} \frac{8 \beta ^{3} + 3}{ \beta ^{2}} \nonumber \]
Minimize the energy with respect to the variational parameter \( \beta\) and report its optimum value and the ground-state energy.
\( \beta = 1\) \( \beta = Minimize (E, \beta )\) \( \beta = 0.90856\) \( E ( \beta ) = 0.688142\)
Plot the coordinate and momentum wavefunctions and the potential energy on the same graph.
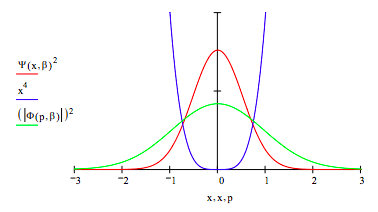
These results demonstrate the uncertainty principle. For the harmonic potential, x2/2, the coordinate and momentum wavefunctions are identical. Compared to the harmonic potential the quartic potential, x4, constrains the spatial wavefunction leading to less uncertainty in position. The uncertainty principle, therefore, requires an increase in the momentum uncertainty. This is clearly revealed in graph above.

