ab initio Basis Sets
- Page ID
- 54032
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Historically, the quantum calculations for molecules were performed as LCAO MO, i.e. Linear Combination of Atomic Orbitals - Molecular Orbitals. This means that molecular orbitals are formed as a linear combination of atomic orbitals:
\[ |\psi_i \rangle = \sum_i^n c_{ij} | \phi _i \rangle\]
where \(|\psi_i \rangle \) is the i-th molecular orbital, \(c_{ij}\) are the coefficients of linear combination, \(\phi_i\) is the \(j^{th}\) atomic orbital, and \(n\) is the number of atomic orbitals.
Strictly speaking, Atomic Orbitals (AO) are solutions of the Hartree-Fock equations for the atom, i.e., a wavefunctions for a single electron in the atom. Anything else is not really an atomic orbital. Some things are similar though, and there is a lot of confusion in the terminology used. Later on, the term atomic orbital was replaced by "basis function" or "contraction," when appropriate. Early, the Slater Type Orbitals (STO's) were used as basis functions due to their similarity to atomic orbitals of the hydrogen atom. They are described by the function depending on spherical coordinates:
\[ | \phi_i (\zeta,n,l,m; r, \theta, \phi) \rangle = N r^{n-1}e^{\zeta r} Y_l^m (\theta,\phi)\]
where \(N\) is a normalization constant, \(\zeta\) is called "exponent". The \(r\), \(\theta\), and \(\phi\) are spherical coordinates, and \(Y_l^m\) is the angular momentum part (function describing "shape"). The \(n\), \(l\), and \(m\) are quantum numbers: principal, angular momentum, and magnetic; respectively.
Unfortunately, functions of this kind are not suitable for fast calculations of necessary two-electron integrals. That is why, the Gaussian Type Orbitals (GTOs) were introduced. You can approximate the shape of the STO function by summing up a number of GTOs with different exponents and coefficients. Even if you use 4 or 5 GTO's to represent STO, you will still calculate your integrals much faster than if original STOs are used. The GTO (called also Cartesian Gaussian) is expressed as:
\[ G_{l, m, n}(x, y,z) = N e^{-\alpha r^2}x^ly^mz^n\]
- where \(N\) is a normalization constant,
- \(\alpha\) is called "exponent" and
- the \(x\), \(y\), and \(z\) are Cartesian coordinates.
The \(l\), \(m\), and \(n\) are not quantum numbers, but simply integral exponents at Cartesian coordinates:
\[r^2 = x^2 + y^2 + z^2\]
Calling Gaussians GTOs is probably a misnomer, since they are not really orbitals; they are simpler functions. In recent literature, they are frequently called Gaussian primitives. The main difference is that \(r^{n-1}\), the preexponential factor, is dropped, the \(r\) in the exponential function is squared, and angular momentum part is a simple function of Cartesian coordinates. The absence of \(r^{n-1}\) factor restricts single Gaussian primitive to approximating only 1s, 2p, 3d, 4f ... orbitals (with no nodes). It was done for practical reasons, namely, for fast integral calculations. However, combinations of Gaussians are able to approximate correct nodal properties of atomic orbitals by taking them with different signs (see below). Following Gaussian functions are possible:
- \( 1s = N e^{-\alpha r^2}\)
- \( 2p_x = N e^{-\alpha r^2}x\)
- \( 2p_y = N e^{-\alpha r^2}y\)
- \( 2p_z = N e^{-\alpha r^2}z\)
- \( 3d_{xx} = N e^{-\alpha r^2}x^2\)
- \( 3d_{xy} = N e^{-\alpha r^2}xy\)
- \( 3d_{xz} = N e^{-\alpha r^2}xz\)
- \( 3d_{yy} = N e^{-\alpha r^2}y^2\)
- \( 3d_{yz} = N e^{-\alpha r^2}yz\)
- \( 3d_{zz} = N e^{-\alpha r^2}z^2\)
- \( 4d_{xxx} = N e^{-\alpha r^2}x^3\)
- \( 4d_{xxy} = N e^{-\alpha r^2}x^2y\)
- \( 4d_{xyz} = N e^{-\alpha r^2}zxyz\)
etc.
Sometimes, the so-called scale factor, \(f\), is used to scale all exponents in the related Gaussians. In this case, the Gaussian function is written as:
\[ G_{l,m,n,f}(x, y,z) = N e^{-\alpha r^2}x^ly^mz^n\]
Be careful not to confuse it with "f" for the f-orbital. The sum of exponents at Cartesian coordinates,
\[L = l+m+n\]
is used analogously to the angular momentum quantum number for atoms, to mark functions as s-type (L=0), p-type (L=1), d-type (L=2), f-type (L=3), etc.
There is a problem with d-type and higher functions. There are only five linearly independent and orthogonal d orbitals, while there are 6 possible Cartesian Gaussians. If we use all six, we are also introducing a 3s type function since:
\[ 3d_{xx} + 3d_{yy} + 3d_{zz} = N ( x^2 + y^2 + z^2) e^{-\alpha r^2} = N r^2e^{-\alpha r^2} = 3s\]
More recently, this effect was studied for sulfur by (Sapio & Topiol, 1989).
Examination of f-type functions shows that there are 10 possible Cartesian Gaussians, which introduce 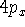 ,
, 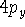 and
and 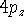 type contamination. However, there are only 7 linearly independent f-type functions. This is a major headache since some programs remove these spurious functions and some do not. Of course, the results obtained with all possible Cartesian Gaussians will be different from those obtained with a reduced set.
type contamination. However, there are only 7 linearly independent f-type functions. This is a major headache since some programs remove these spurious functions and some do not. Of course, the results obtained with all possible Cartesian Gaussians will be different from those obtained with a reduced set.
Contractions
Gaussian primitives are usually obtained from quantum calculations on atoms (i.e. Hartree-Fock or Hartree-Fock plus some correlated calculations, e.g. CI). Typically, the exponents are varied until the lowest total energy of the atom is achieved (Clementi et al., 1990). In some cases, the exponents are optimized independently. In others, the exponents are related to each other by some equation, and parameters in this equation are optimized (e.g. even-tempered or "geometrical" and well-tempered basis sets). The primitives so derived describe isolated atoms and cannot accurately describe deformations of atomic orbitals brought by the presence of other atoms in the molecule. Basis sets for molecular calculations are therefore frequently augmented with other functions which will be discussed later.
For molecular calculations, these Gaussian primitives have to be contracted, i.e., certain linear combinations of them will be used as basis functions. The term contraction means "a linear combination of Gaussian primitives to be used as basis function." Such a basis function will have its coefficients and exponents fixed. The contractions are sometimes called Contracted Gaussian Type Orbitals (CGTO). To clear things up, a simple example from Szabo and Ostlund, 1989. The coefficients and exponents of Gaussian expansion which minimizes energy of the hydrogen atom were derived by Huzinaga, 1965. Four s-type Gaussians were used to represent 1s orbital of hydrogen as:
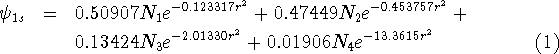
\(N_i\) is a normalization constant for a given primitive. In the case of Gaussians of type s it is equal to \((2\alpha/\pi)^{3/4}}.
These primitives may be grouped in 2 contractions. The first contraction contains only 1 primitive:
\[ | \phi_1 \rangle = N_1 e^{-0.123317 r^2}\]
Three primitives are present in the second contraction:
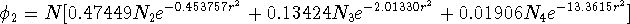
\(N\) is a normalization constant for the whole contraction.
In this case, 4 primitives were contracted to 2 basis functions. It is frequently denoted as (4s)  [2s] contraction (some use (4s)/[2s] notation). The coefficients in function
[2s] contraction (some use (4s)/[2s] notation). The coefficients in function 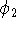 are then fixed in subsequent molecular calculations.
are then fixed in subsequent molecular calculations.
The way in which contractions are derived is not easy to summarize. Moreover, it depends upon the intended use for the basis functions. It is a good idea to always read the original paper which describes the way in which contractions have been done. Some basis sets are good for geometry and energies, some are aimed at properties (e.g. polarizability), some are optimized only with Hartree-Fock in mind, and some are tailored for correlated calculations. Finally, some are good for anions and other for cations and neutral molecules. For some calculations, a good representation of the inner (core) orbitals is necessary (e.g. for properties required to analyze NMR spectrum), while other require best possible representation of valence electrons. WHY ARE CONTRACTIONS DONE
Obviously, the best results could be obtained if all coefficients in Gaussian expansion were allowed to vary during molecular calculations. Moreover, the computational effort (i.e. "CPU time") for calculating integrals in the Hartree-Fock procedure depends upon the 4th power in the number of Gaussian primitives. However, all subsequent steps depend upon the number of basis functions (i.e. contractions). Also, the storage required for integrals (when Direct SCF is not used) is proportional to the number of basis functions (not primitives!). Frequently the disk storage and not the CPU time is a limiting factor. The CPU time requirements are more acute when post-Hartree- Fock (e.g. correlated methods) are used, since the dependence upon the number of basis functions here is more steep than the 4th power.
There are two basic forms of contractions, namely "segmented" and "general". The segmented contractions are disjointed, i.e., given primitive appears only in one contraction. The example given above (4s)  [2s] is a segmented contraction. Occasionally, one or two primitives may appear in more than one contraction, but this is an exception to the rule. The general contractions, on the contrary, allow each of the primitives to appear in each basis function (contraction). The segmented contractions are far more popular and will be described first. The reason for their popularity is not that they are better, but simply, that the most popular ab initio packages do not implement efficient integral calculations with general contractions. The computer code to perform integral calculations with general contractions is much more complex than that for the segmented case.
[2s] is a segmented contraction. Occasionally, one or two primitives may appear in more than one contraction, but this is an exception to the rule. The general contractions, on the contrary, allow each of the primitives to appear in each basis function (contraction). The segmented contractions are far more popular and will be described first. The reason for their popularity is not that they are better, but simply, that the most popular ab initio packages do not implement efficient integral calculations with general contractions. The computer code to perform integral calculations with general contractions is much more complex than that for the segmented case.
SEGMENTED CONTRACTIONS. TERMS AND NOTATION
The segmented basis sets are usually structured in such a way that the most diffuse primitives (primitives with the smallest exponent) are left uncontracted (i.e. one primitive per basis function). More compact primitives (i.e. those with larger exponents) are taken with their coefficients from atomic Hartree-Fock calculations and one or more contractions are formed. Then the contractions are renormalized. Sometimes different contractions share one or two functions (the most diffuse function(s) from the first contraction enter the next one).
Cartesian Gaussians are grouped in shells coresponding to the same value of angular momentum quantum number. Of course, these shells should not be confused with electron shells (i.e. electrons with the same principal quantum number: K  n=1, L
n=1, L  n=2, etc.). Quantum chemists must have run out of words on this one. And hence, we have s-shell, p-shell, d-shell, f-shell, g-shell, etc. The shell is a collection of Cartesian Gaussians that have the same L (see definition of Cartesian Gaussian above). Strictly speaking, the s-shell is a collection of s type Gaussians; p-shell is a collection of p-type Gaussians; d-shell is a collection of d-type Gaussians; and so on. Of course, combining primitives belonging to different shells within the same contraction does not make sense because primitives from different shells are orthogonal.
n=2, etc.). Quantum chemists must have run out of words on this one. And hence, we have s-shell, p-shell, d-shell, f-shell, g-shell, etc. The shell is a collection of Cartesian Gaussians that have the same L (see definition of Cartesian Gaussian above). Strictly speaking, the s-shell is a collection of s type Gaussians; p-shell is a collection of p-type Gaussians; d-shell is a collection of d-type Gaussians; and so on. Of course, combining primitives belonging to different shells within the same contraction does not make sense because primitives from different shells are orthogonal.
But even here there is a room for more confusion. Many basis sets use the same exponents for functions corresponding to the same principal quantum number, i.e., electronic shell. STO-3G is an example, as well as other basis sets from Pople's group. Atoms of the first and second row (i.e. Li - Ne, Na - Cl) have the same exponents for s- and p-type Gaussians formally associated with a given electron shell of the isolated atom. For the basis sets in which s- and p-type functions share the same exponents, the term SP-shell is used. Sometimes term L-shell is used by analogy to the 2nd electron shell. This approximation works very well in practice. Moreover, it is possible to write efficient code for calculating integrals for such cases. It is important to stress here that the distinction between inner orbitals and valence orbitals is kind of arbitrary and lingers from the past era of Slater orbitals. Contrac- tions consisting of primitives with large exponents are associated with inner atomic orbitals while more diffuse fuctions are allied with valence orbitals. Basis functions are not usually atomic orbitals, and in many cases, they do not even resemble orbitals of isolated atoms. In fact, examining coefficients of molecular orbitals frequently reveals that these "core" basis functions contribute substantially to the Highest Occupied Molecular Orbital (HOMO). It comes as a consequence of the fact that basis functions on a given center are usually not orthogonal to each other and "core" basis functions on different centers overlap to a great extent - situation not likely to occur with true atomic orbitals.
The early Gaussian contractions were obtained by a least square fit to Slater atomic orbitals. The number of contractions (not primitives!) used for representing a single Slater atomic orbital (i.e. zeta) was a measure of the goodness of the set. From this era we have terms like single zeta (SZ), double zeta (DZ), triple zeta (TZ), quadruple zeta (QZ), etc. In the minimal basis set (i.e. SZ) only one basis function (contraction) per Slater atomic orbital is used. DZ sets have two basis functions per orbital, etc. Since valence orbitals of atoms are more affected by forming a bond than the inner (core) orbitals, more basis functions are assigned frequently to describe valence orbitals. This prompted development of split-valence (SV) basis sets, i.e., basis sets in which more contractions are used to describe valence orbitals than core orbitals. That more basis functions are assigned to valence orbitals does not mean the valence orbitals incorporate more primitives. Frequently, the core orbitals are long contractions consisting of many primitive Gaussians to represent well the "cusp" of s type function at the position of the nucleus. The "zeta" terminology is often augmented with a number of polarization functions which will be described later. So, DZP means double-zeta plus polarization, TZP stands for triple-zeta plus polarization, etc. Sometimes the number of polarization functions is given, e.g. TZDP, TZ2P, TZ+2P stands for triple-zeta plus double polarization. Letter V denotes split valence basis sets, e.g., DZV represents basis set with only one contraction for inner orbitals, and two contractions for valence orbitals. The creativity here is enormous and spontaneous.
The minimal basis set is the smallest possible set, i.e., it contains only one function per occupied atomic orbital in the ground state. Actually, it always includes all orbitals from partially occupied subshells and valence p-type functions for elements from the first 2 groups of the periodic table. So for Li and Be atoms it has 2 s-type contractions and 1 p-type contraction. Minimal basis set for S atom has 3 s-type contractions and 2 p-type contractions. The most popular minimal basis sets are the STO-nG, where n denotes number of primitives in the contraction. These sets were obtained by least square fit of the combination of n Gaussian functions to a Slater type orbital of the same type with zeta = 1.0, For this set additional constraint is used, that exponents of corresponding Gaussian primitives are the same for basis functions describing orbitals with the same principal quantum number (e.g. the same primitives are used for 2s and 2p function). Then, these exponents are multipled by the square of zeta in the Slater orbital which described best the set of molecules. For details, see Szabo and Ostlund (1989) or original literature quoted on page 71 of Hehre et al. (1986). The STO-3G (i.e. 3 primitives per each function) is the most widely used set.
For other sets a more complicated notation needs to be used to specify the number of primitives and contractions explicitly. The parentheses () embrace the number of primitives that are given in the order of angular momentum quantum number. Square brackets [] are used to specify the number of resulting contractions. For example: (12s,9p,1d) means 12 primitives on s-shell, 9 primitives on p-shell, and 1 primitive on d-shell. This is sometimes abbreviated even further by skipping the shell symbols (12,9,1). The [5,4,1] means that s-shell has 5 contractions, p-shell has 4 contractions and d-shell has 1 contraction. To denote how contractions were performed, the following notation is frequently used: (12,9,1)  [5,4,1] or (12,9,1)/[5,4,1] or (12s,9p,1d)
[5,4,1] or (12,9,1)/[5,4,1] or (12s,9p,1d)  [5s,4p,1d]. This means that 12 s-type primitives were contracted to form 5 s-type contractions, 9 p-primitives were contracted to 4 basis functions and 1 d-primitive was used as a basis function by itself. Note of caution here. The statement "9 p-primitives were contracted to 4 basis functions" actually means that 12 basis functions were created. Each p-type basis functions has 3 variants:
[5s,4p,1d]. This means that 12 s-type primitives were contracted to form 5 s-type contractions, 9 p-primitives were contracted to 4 basis functions and 1 d-primitive was used as a basis function by itself. Note of caution here. The statement "9 p-primitives were contracted to 4 basis functions" actually means that 12 basis functions were created. Each p-type basis functions has 3 variants: 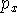 ,
, 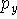 , and
, and 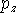 which differ in their Cartesian part (i.e., angular part). The same is true for d-, f-, and higher angular momentum functions.
which differ in their Cartesian part (i.e., angular part). The same is true for d-, f-, and higher angular momentum functions.
The notation above does not say how many primitives are used in each contraction. The more elaborate notation explicitly lists the number of primitives in each contraction. For example: (63111,4311,1) means that there are 5 s-type contractions consisting of 6, 3, 1, 1 and 1 primitives, repectively. The p-shell consists of 4 basis functions with 4, 3, 1 and 1 primitives, and d-shell has 1 uncontracted primitive. Sometimes slashes are used instead of commas: (63111/4311/1). This is sometimes "abbreviated" to (633x1,432x1,1). There is also another notation to denote contractions as L(i/j/k/l...) for each shell corresponding to angular momentum quantum number equal to L. For example, the (63111,4311,1) basis set is represented as: s(6/3/1/1/1), p(4/3/1/1), and d(1). Of course, variants of this notation are also used. You can find this set written as: (6s,3s,1s,1s,1s/4p,3p,1p,1p/1d) or (6,6,1,1,1/4,3,1,1/1) or [6s,3s,1s,1s,1s/4p,3p,1p,1p/1d] (sic!). I did not study the combinatorics of this, but quantum chemists might have exhausted all combinations of digits, brackets and commas. However, if you ask 10 quantum chemists which notation is considered standard, you will get 20 different answers.
Sometimes the same primitive is incorporated in two contractions (i.e. is "doubled"); e.g., the popular Chandler-McLean (12,9) sulphur basis set (McLean and Chandler, 1980) is contracted as [6,5] with the scheme (631111,42111). If you count primitives contained in contractions for the s-shell, you get 13 primitives instead of 12. This means that one primitive is shared (i.e. doubled) between two contractions, 6- and 3-contraction in this case. It would make little sense to share a primitive between 6- and 1- or 3- and 1-contrac- tion since such contraction whould yield the basis set of the same quality as "undoubled" one. In some cases the smallest exponent from the first contraction is repeated in the next contraction as the largest one. In the above case, the basis set formaly represents a general contraction, but since only one function is doubled, it is used frequently in programs that do not support general contractions.
By convention, the primitives are listed as exponents and coefficients starting from the highest exponent. In tables of exponents and coefficients the numbers are frequently represented in an interesting way, with powers of 10 in parentheses, e.g. 457.3695 is denoted as 4.573696(+2) and 0.01403732 as 1.403732(-2). Of course, it is obvious if you know it. The typical basis set specification (Gordon, 1980, modified) is given below as an example:
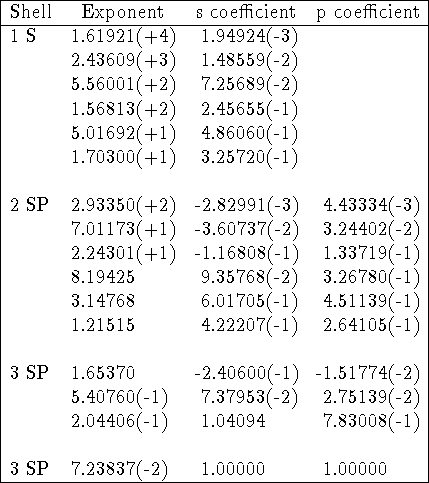
Table: 66-31G basis set for silicon.
In the example above, corresponding exponents for s- and p-type contractions are equal but coefficients in s- and p-type contractions are different. Gaussian primitives are normalized here since coefficients for basis functions consisting of one primitive (last row) are exactly 1.0. The basis set above represents the following contraction (16s,10p)  [4s,3p] or (6631,631).
[4s,3p] or (6631,631).
To add to the confusion, the coefficients are sometimes listed either as original coefficients in atomic orbitals or are renormalized for the given contraction. In some cases coefficients are premultiplied by a normalization constant for a Gaussian primitive, but in most cases it is assumed that 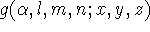 is already normalized (and this is the correct way!). You have to be prepared for surprises when entering explicit basis sets from the literature. Program manuals neglect basis sets description assuming it is common knowledge. When specifying structure of the basis sets for the entire molecule, slashes are used to separate information for different atoms (or rows, if basis sets for a given row have the same structure for all atoms). The information is given starting from the heaviest atoms. For example, the basis set for water would be given as (10s,5p,1d/5s,1p)
is already normalized (and this is the correct way!). You have to be prepared for surprises when entering explicit basis sets from the literature. Program manuals neglect basis sets description assuming it is common knowledge. When specifying structure of the basis sets for the entire molecule, slashes are used to separate information for different atoms (or rows, if basis sets for a given row have the same structure for all atoms). The information is given starting from the heaviest atoms. For example, the basis set for water would be given as (10s,5p,1d/5s,1p)  [4s,2p,1d/2s,1p] in which case the contractions for oxygen atoms are (10,5p,1d)
[4s,2p,1d/2s,1p] in which case the contractions for oxygen atoms are (10,5p,1d)  [4s,2p,1d] and for the hydrogen (5s,1p)
[4s,2p,1d] and for the hydrogen (5s,1p)  [2s,1p].
[2s,1p].
Pople's basis sets
A different convention was adopted by Pople and coworkers. The basis set structure is given for the whole molecule, rather than particular a atom. This notation emphasizes also a split valence (SV) nature of these sets. Symbols like n-ijG or n-ijkG can be encoded as: n - number of primitives for the inner shells; ij or ijk - number of primitives for contractions in the valence shell. The ij notations describes sets of valence double zeta quality and ijk sets of valence triple zeta quality. Generally, in basis sets derived by Pople's group, the s and p contractions belonging to the same "electron shell" (i.e. corresponding formally to the same principal quantum number n) are folded into a sp-shell. In this case, number of s-type and p-type primitives is the same, and they have identical exponents. However, the coefficients for s- and p-type contractions are different.
Now, some examples. The 4-31G basis set for hydrogen (hydrogen has only valence electrons!) is a contraction (31) or (4s)  [2s]; for first row atoms (8s,4p)
[2s]; for first row atoms (8s,4p)  [3s,2p] or (431,31); and for 2nd row atoms the contraction scheme is (12s,8p)
[3s,2p] or (431,31); and for 2nd row atoms the contraction scheme is (12s,8p)  [4s,3p] or (4431,431). For water molecule, these contractions could be encoded as (431,31/31). The 6-311G set represents the following contractions for water (6311,311)/(311) or (11s,5p/5s)
[4s,3p] or (4431,431). For water molecule, these contractions could be encoded as (431,31/31). The 6-311G set represents the following contractions for water (6311,311)/(311) or (11s,5p/5s)  [4s,3p/3s].
[4s,3p/3s].
The Pople's basis sets can also be augmented with d type polarization functions on heavy atoms only (n-ijG* or n-ijkG*) or on all atoms, with p-functions on hydrogens (n-ijG** or n-ijkG**). In methane, the 4-31G* encodes following split (431,31,1)/(31) or (8s,4p,1d/4s)  [3s,2p,1d/2s], while 6-311G** for HCN molecule would involve following contractions: (6311,311,1)/(311,1) or (11s,5p,1d/5s,1p)
[3s,2p,1d/2s], while 6-311G** for HCN molecule would involve following contractions: (6311,311,1)/(311,1) or (11s,5p,1d/5s,1p)  [4s,3p,1d/3s,1p]. Currently, the 6-311G keyword for second row atoms, as implemented in Gaussian90 program, does not actually correspond to the true 6-311G set. It is explicitly mentioned in Gaussian90 manual. For these atoms, 6-311G keyword defaults to MC basis sets (McLean and Chandler, 1980) of the type (12s,9p)
[4s,3p,1d/3s,1p]. Currently, the 6-311G keyword for second row atoms, as implemented in Gaussian90 program, does not actually correspond to the true 6-311G set. It is explicitly mentioned in Gaussian90 manual. For these atoms, 6-311G keyword defaults to MC basis sets (McLean and Chandler, 1980) of the type (12s,9p)  [6,5] with contraction scheme (631111,42111). Note, that one of the s-type functions is doubled. The basis sets for P, S and Cl correspond actually to the "anion" basis sets in the original paper since "these were deemed to give better results for neutral molecules as well."
[6,5] with contraction scheme (631111,42111). Note, that one of the s-type functions is doubled. The basis sets for P, S and Cl correspond actually to the "anion" basis sets in the original paper since "these were deemed to give better results for neutral molecules as well."
Sometimes, for atoms of the second row nm-ijG notation is used. For example, 66-31G means that there is:
- 1 function containing 6 primitives on the innermost s-shell;
- 1 set of functions belonging to the inner SP-shell (i.e. 2SP shell), each consisting of 6 Gaussian primitives (i.e. 1 s-type function and
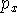 ,
, 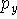 ,
, 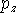 functions consisting of 6 primitives with the same exponents). Note though that coefficients in s and p type contractions are different,
functions consisting of 6 primitives with the same exponents). Note though that coefficients in s and p type contractions are different, - 2 sets of SP functions for valence SP shell (one set consisting of contractions with 3 primitives and the other with 1 primitive).
It is possible to write this as (16s,10p)  [4s,3p] or in more details as (6631,631) contraction scheme or alternatively as s(6/6/3/1), p(6/3/1).
[4s,3p] or in more details as (6631,631) contraction scheme or alternatively as s(6/6/3/1), p(6/3/1).
Polarization and diffuse functions
The original contractions derived from atomic Hartree-Fock calculations are frequently augmented with other functions. The most popular are the polarization and diffuse functions. The polarization functions are simply functions having higher values of L than those present in occupied atomic orbitals for the corresponding atom. At least for me, there is some ambiguity here, since for lithium, the p-type functions are not considered polarization functions, while for sulphur, the d-functions are considered polarization functions. In both cases these orbitals are not populated in the ground electronic state of the atom. The reason for including p-type functions in the Li and Be atoms, even in the minimal basis sets, is prac- tical, however. Without these functions, the results are extremely poor. The reason for not including d-type functions for sulphur should be the same as for other atoms, i.e., you can obtain reasonable results without them. I wish, I could believe that.
The exponents for polarization functions cannot be derived from Hartree-Fock calculations for the atom, since they are not populated. However, they can be estimated from correlated calculations involving atoms. In practice, however, these exponents are estimated "using well established rules of thumb or by explicit optimization" (Dunning, 1989).
The polarization functions are important for reproducing chemical bonding. They were frequently derived from optimizing exponents for a set of molecules. They should also be included in all correlated calculations. They are usually added as uncontracted Gaussians. It is important to remember that adding them is costly. Augmenting basis set with d type polarization functions adds 5 (or 6) basis function on each atom while adding f type functions adds 7 (or 10, if spurious combinations are not removed). This brings us to the problem of specifying the number of d, f, g, etc. polarization functions in a form of some compact notation. Unfortunately, there is no provision for this information in the notations described above. Pople's 6-31G* basis uses 6 d type functions as polarization functions, while 6-311G* uses 5 of them. The () notation is no better. If the paper does not say explicitly how many d or f functions are used, you are on your own. The only way to find out is to repeat the calcula- tions or contact the author. Many papers do not specify this important information. The Pople's group introduced yet another more general notation to encode type of polarization functions. The easiest way is to explain an example. The 6-31G** is synonymous to 6-31G(d,p); the 6-311G(3d2f,2p) represents 6-311G set augmented with 3 functions of type d and 2 functions of type f on heavy atoms, and 2 functions of type p on hydrogens or specifically (6311,311,111,11)/(311,11), i.e. (11s,4p,3d,2f/5s,2p)  [4s3p3d2f/3s2p] contraction. The 6 d-type polarization function is added to 6-31G set, while only 5 to 6-311G. For both 6-31G and 6-311G set, f-type functions are added in groups of 7. Polarization functions are, as a rule, used uncontracted. More information can be found in the following papers: (Dunning, 1989), (Francl et al., 1982), (Gutowski et al., 1987), (Jankowski, 1985), (Krishnan et al., 1980).
[4s3p3d2f/3s2p] contraction. The 6 d-type polarization function is added to 6-31G set, while only 5 to 6-311G. For both 6-31G and 6-311G set, f-type functions are added in groups of 7. Polarization functions are, as a rule, used uncontracted. More information can be found in the following papers: (Dunning, 1989), (Francl et al., 1982), (Gutowski et al., 1987), (Jankowski, 1985), (Krishnan et al., 1980).
The basis sets are also frequently augmented with the so-called diffuse functions. The name says it all. These Gaussians have very small exponents and decay slowly with distance from the nucleus. Diffuse Gaussians are usually of s and p type, however sometimes diffuse polarization functions are also used. Diffuse functions are necessary for correct description of anions and weak bonds (e.g. hydrogen bonds) and are frequently used for calculations of properties (e.g. dipole moments, polarizabilities, etc.). For the Pople's basis sets the following notaton is used: n-ij+G, or n-ijk+G when 1 diffuse s-type and p-type Gaussian with the same exponents are added to a standard basis set on heavy atoms. The n-ij++G, or n-ijk++G are obtained by adding 1 diffuse s-type and p-type Gaussian on heavy atoms and 1 diffuse s-type Gaussian on hydrogens. For example, the 6-31+G* represents (6311,311,1)/(31) or (11s,5p,1d/4s)  [4s,3p,1d/2s]. The 6-311+G(2d1f,2p1d) stands for (63111,3111,11,1)/(311,11,1) split, or (12s,6p,2d,1f)
[4s,3p,1d/2s]. The 6-311+G(2d1f,2p1d) stands for (63111,3111,11,1)/(311,11,1) split, or (12s,6p,2d,1f)  [5s,2p,1d]. For more information about diffuse functions see, for example (Clark et al., 1983), (Del Bene, 1989), and (Frisch et al., 1984).
[5s,2p,1d]. For more information about diffuse functions see, for example (Clark et al., 1983), (Del Bene, 1989), and (Frisch et al., 1984).
To calculate total number of primitives/basis functions in your molecule, you sum up the number of primitives/basis functions for each partaking atom. As an example, let us compute the number of functions for H2SO3 molecule assuming the use of Gaussian90 program. The 6-311++G(3df,2p) basis set is used as an example. In this case the reduced set of d and f Gaussians is used, i.e., 5 d-type functions and 7 f-type functions. It corresponds to the following contractions:
- S: (6311111,421111,111,1)
- (for sulphur, Gaussian90 defaults to McLean-Chandler basis set (631111,42111) for sulphur anion which is augmented with one diffuse s and one diffuse p function, and three d and one f polarization functions)
- O: (63111,3111,111,1)
- (this is 6-311G for oxygen augmented with one s- and one p-type diffuse function, and three d and one f polarization function)
- H: (3111,11)
- (this is 6-311G augmented with one diffuse s and two p-functions for polarization)
Number of basis functions:
- S:
- 7 s-type functions, 6
 3 p-type functions, 3
3 p-type functions, 3  5 d-type functions and 1
5 d-type functions and 1  7 f-type functions
7 f-type functions - O:
- 5 s-type functions, 4
 3 p-type functions, 3
3 p-type functions, 3  5 d-type functions and 1
5 d-type functions and 1  7 f-type functions
7 f-type functions - H:
- 4 functions of type s and 2
 3 functions of type p (there are 3 p function for each p type contraction, i.e.
3 functions of type p (there are 3 p function for each p type contraction, i.e. 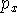 ,
, 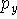 ,
, 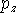 )
)
H2SO3 = (4 + 2  3)
3)  2 + (7 + 6
2 + (7 + 6  3 + 3
3 + 3  5 + 1
5 + 1  7) + (5 + 4
7) + (5 + 4  3 + 3
3 + 3  5 + 1
5 + 1  7)
7)  3 = 184
3 = 184
Total number of Gaussian primitives:
- S:
- 1
 (6+3+1+1+1+1+1) + 3
(6+3+1+1+1+1+1) + 3  (4+2+1+1+1+1) + 5
(4+2+1+1+1+1) + 5  (1+1+1) + 7
(1+1+1) + 7  1 = 66
1 = 66 - O:
- 1
 (6+3+1+1+1) + 3
(6+3+1+1+1) + 3  (3+1+1+1) + 5
(3+1+1+1) + 5  (1+1+1) + 7
(1+1+1) + 7  1 = 52
1 = 52 - H:
- 1
 (3+1+1+1) + 3
(3+1+1+1) + 3  (1+1) = 12
(1+1) = 12
H2SO3 = 2  12 + 66 + 3
12 + 66 + 3  52 = 246 primitives.
52 = 246 primitives.
GENERAL CONTRACTIONS. TERMS AND NOTATION
Raffenetti (1973) introduced term "general contraction" for basis sets in which the same Gaussian primitives can appear in several basis functions. In general contraction scheme, the basis functions are formed as different linear combinations of the same primitives. This is clearly in contrast with the segmented scheme described above. Please do not confuse general contrac- tions with a term "general basis set" used in some program manuals to denote "user defined segmented basis sets".
General contractions have many advantages from the theoretical point of view. The most important is that they might be chosen to approximate true atomic orbitals which makes interpretation of coefficients in molecular orbitals meaningful. Also for correlated calculations their performance is praised (Almlof and Taylor, 1987; Almlof et al., 1988; Dunning, 1989) Secondly, they can be chosen in a more standard way than segmented contractions, either as true atomic orbitals obtained from Hartree- Fock calculations for the atom with uncontracted primitives as basis functions, or as Atomic Natural Orbitals (ANO). For description of ANO's consult papers by Almlof and coworkers or read appropriate chapter in Szabo and Ostlund, (1989). The only problem with general contractions is that only a few programs support them. The code for integral package is much more complicated in this case, since it has to work on a block of integrals at each time, to compute the contribution from the given primitive set only once. Of course, you can always enter general contractions as "user defined segmented basis sets," by repeating the same primitives over and over again in different contractions. This will cost you, however, immensely in computer time at the integral computation stage. Remember, the time required for calculating integrals is proportional to the 4th power in the number of Gaussian primitives, and most programs assume that primitives entering different contractions are different.
As an example, the general contractions of (8s4p) set of primitives for oxygen by Huzinaga et al., 1971 (taken from: Raffenetti, 1973).
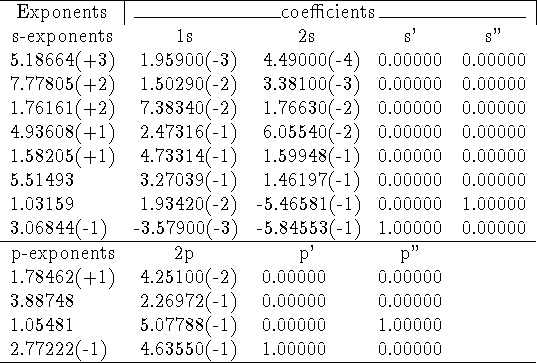
In the table above, integer numbers in parantheses denote powers of 10 multiplying number in front of them.
The set above can be described as (8s,4p)  [4s,3p] contraction. Clearly, the notation giving the number of primitives in each contraction as (abcd...) is not really useful here. It is especially true with newer sets implementing general contractions, where each primitive has all nonzero coefficients in practically every column.
[4s,3p] contraction. Clearly, the notation giving the number of primitives in each contraction as (abcd...) is not really useful here. It is especially true with newer sets implementing general contractions, where each primitive has all nonzero coefficients in practically every column.
EFFECTIVE CORE POTENTIALS (EFFECTIVE POTENTIALS)
It was known for a long time that core (inner) orbitals are in most cases not affected significantly by changes in chemical bonding. This prompted the development of Effective Core Potential (ECP) or Effective Potentials (EP) approaches, which allow treatment of inner shell electrons as if they were some averaged potential rather than actual particles. ECP's are not orbitals but modifications to a hamiltonian, and as such are very efficient computationally. Also, it is very easy to incorporate relativistic effects into ECP, while all-electron relativistic computations are very expensive. The relativistic effects are very important in describing heavier atoms, and luckily ECP's simplify calculations and at the same time make them more accurate with popular non-relativistic ab initio packages (provided that such packages have support for ECP's). The core potentials can only be specified for shells that are filled.
[ ANDREAS SAVIN correction: You state that core potentials can only be specified for filled shells. In fact, they can be also defined for open shell cores (see, for example, the pseudopotentials for the lanthanides, Dolg et al., Theor. Chim. Acta 75 (1989) 173 ). We would like to use this opportunity to point out that pseudopotentials and corresponding valence basis sets are available from us, not only for the lanthanides, but for all the elements up to Uranium. A comparison of our pseudopotentials with other ones shows their quality (see, e.g., Andrae et al., Theor. Chim. Acta 78 (1991) 247).]
For the rest of electrons (i.e. valence electrons), you have to provide basis functions. These are special basis sets optimized for the use with specific ECP's. These basis sets are usually listed in original papers together with corresponding ECP's. Some examples of papers describing ECP's: (Durand and Bartelat, 1975), (Hay and Wadt, 1985ab), (Hurley et al., 1986), (Pacios and Christensen, 1985), (Stevens ey al., 1984), (Wadt and Hay, 1985), (Walace et al., 1991). The ECP are tabulated in the literature as parameters of the following expansion:
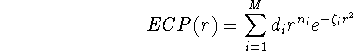
where M is the number of terms in the expansion, 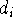 is a coefficient for each term, r denotes distance from nucleus,
is a coefficient for each term, r denotes distance from nucleus,  is a power of r for the i-th term, and
is a power of r for the i-th term, and 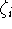 represents the exponent for the i-th term.
represents the exponent for the i-th term.
To specify ECP for a given atomic center, you need to include typically: the number of core electrons that are substituted by ECP, the largest angular momentum quantum number included in the potential (e.g., 1 for s only, 2 for s and p, 3 for s, p, and d; etc.), and number of terms in the "polynomial Gaussian expansion" shown above. For each term in this expansion you need to specify: coefficient ( 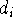 ), power of r (
), power of r (  ) and exponent in the Gaussian function (
) and exponent in the Gaussian function ( 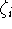 ). Also you need to enter basis set for valence electrons specific to this potential. As a result of applying the ECP's you drastically reduce number of needed basis functions, since only functions for valence electrons are required. In many cases, it would simply be impossible to perform some calculations on systems involving heavier elements without ECP's (try to calculate number of functions in TZ2P basis set for e.g. U, and you will know why).
). Also you need to enter basis set for valence electrons specific to this potential. As a result of applying the ECP's you drastically reduce number of needed basis functions, since only functions for valence electrons are required. In many cases, it would simply be impossible to perform some calculations on systems involving heavier elements without ECP's (try to calculate number of functions in TZ2P basis set for e.g. U, and you will know why).
REFERENCES
- R. Ahlrichs, P.R.Taylor, 1981, "The choice of Gaussian basis sets for molecular electronic structure calculations," J.Chim.Phys, 78, 315-324.
- J. Almlof, P.R. Taylor, 1987, "General contraction of Gaussian basis sets. I. Atomic natural orbitals for first- and second-row atoms," J. Chem. Phys. 86, 4070-4077.
- J. Almlof, T. Helgaker, P.R. Taylor, 1988, "Gaussian basis sets for high- quality ab initio calculations," J. Phys. Chem., 92, 3029-3033.
- J. Andzelm, M. Klobukowski, E. Radzio-Andzelm, Y. Saski, H. Tatewaki, 1984, "Gaussian Basis Sets for Molecular Calculations," (S. Huzinaga, Editor), Elsevier, Amsterdam.
- T. Clark, J. Chandrasekhar, G.W. Spitznagel, P.v.R. Schleyer, (1983), "Efficient diffuse function-augmented basis sets for Anion Calculations. III. The 3-21+G set for first-row elements, Li-F," J. Comput. Chem., 4, 294-301.
- E.Clementi, S.J.Chakravorty, G.Corongiu, V.Sonnad, 1990, "Independent Electron Models: Hartree-Fock for Many-Electron Atoms," pp. 47-140, in: "MOTECC-90 Modern Techniques in Computational Chemistry (E.Clementi, Ed.), Escom, Leiden 1990, ISBN-90-72199-07-3.
- J.E. Del Bene, 1989, "An ab initio molecular orbital study of the structures and energies of neutral and charged bimolecular complexes of
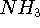 with hydrides
with hydrides 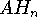 (A = N, O, F, P, S, and Cl)," J. Comput. Chem. 10, 603-615.
(A = N, O, F, P, S, and Cl)," J. Comput. Chem. 10, 603-615. - T.H. Dunning, P.J. Hay, 1977, "Gaussian basis sets for molecular calculations," in: "Modern Theoretical Chemistry," vol. 3. Ed. H.F. Schaefer III, pp. 1-28, Plenum Press, New York.
- T.H. Dunning, Jr., 1989, "Gaussian basis sets for use in correlated molecular calculations," J.Chem.Phys. 90, 1007-1023.
- P. Durand, J.-C. Barthelat, 1975, "A theoretical method to determine atomic pseudopotentials for electronic structure calculations of molecules and solids," Theor. Chim. Acta(Berl.) 38, 283-302.
- D. Feller, E.R. Davidson, 1986, "Basis set selection for molecular calculations," Chemical Reviews, 86, 681-696.
- D. Feller, E.R. Davidson, 1990, "Basis Sets for Ab Initio Molecular Orbital Calculations and Intermolecular Interactions," pp. 1-43, in: "Reviews in Computational Chemistry" (Editors:Kenny B. Lipkowitz and Donald B. Boyd), VCH, New York.
- M.M. Francl, J.S. Binkley, M.S. Gordon, D.J. DeFrees, J.A. Pople, 1982, "Self- consistent molecular orbital methods. XXIII. A polarization-type basis set for second-row element," J.Chem.Phys. 77, 3654-3665.
- M.J. Frisch, J.A. Pople, J.S. Binkley, 1984, "Self-consistent molecular orbital methods 25. Supplementary functions for Gaussian Basis Sets," J. Chem. Phys. 80, 3265-3269.
- M.S. Gordon, 1980, "The isomers of silacyclopropane," Chem. Phys. Lett., 76, 163-168.
- M. Gutowski, F.B. Van Duijneveldt, G. Chalasinski, L. Piela, 1987, "Proper correction for the basis set superposition error in SCF calculations of intermolecular calculations," Mol. Phys. 61, 233-247.
- P.J. Hay, W.R. Wadt, 1985a, "Ab Initio effective core potentials for molecular calculations. Potentials for transition metal atoms Sc to Hg," J. Chem. Phys. 82, 271-283.
- P.J. Hay, W.R. Wadt, 1985b, "Ab Initio effective core potentials for molecular calculations. Potentials for K to Au including outermost core orbitals," J. Chem. Phys. 82, 299-310.
- W.J. Hehre, L. Radom, P.v.R Schleyer, J.A. Pople, 1986, "Ab Initio Molecular Orbital Theory," Willey & Sons, New York.
- M.M. Hurley, L.F. Pacios, P.A. Christiansen, R.B. Ross, W.C. Ermler, 1986, "Ab initio relativistic effective potentials with spin-orbit operators. II. K through Kr," J. Chem. Phys. 84, 6840-6853.
- S. Huzinaga, 1965, "Gaussian-type functions for polyatomic systems," J. Chem. Phys., 42, 1293-1302.
- S. Huzinaga, D. McWilliams, B. Domsky, 1971, "Approximate Atomic Function," J. Chem. Phys. 54, 2283-2284.
- K. Jankowski, R. Becherer, P. Scharf, H. Schiffer, R. Ahlrichs, 1985, "The impact of higher polarization basis functions on molecular ab initio results," J. Chem. Phys. 82, 1413-1419.
- R. Krishnan, J.S. Binkley, R. Seeger, J.A. Pople, 1980, "Self-consistent orbital methods. XX. A basis set for correlated wave functions," J. Chem. Phys. 72, 650-654.
- A.D. McLean, G.S. Chandler, 1980, "Contracted Gaussian basis sets for molecular calculations. I. Second row atoms, Z=11-18," J. Chem. Phys., 72, 5639-5648.
- L.F. Pacios, P.A. Christiansen, 1985, "Ab initio relativistic effective potentials with spin-orbit operators. I. Li through Ar.
- R. Poirier, R. Kari, I.G. Csizmadia, 1985, "Handbook of Gaussian Basis Sets," Elsevier Science, New York.
- R.C. Raffenetti, 1973, "General contraction of Gaussian atomic orbitals: Core, valence, polarization and diffuse basis sets; Molecular integral evaluation," J. Chem. Phys, 58, 4452-4458.
- M. Sabio, S. Topiol, 1989, " 3s- versus 1s-type gaussuan primitives: Modification of the 3-21G(*) basis set for sulphur atom. J. Comput. Chem., 10, 660-672.
- W.J. Stevens, H. Bash, M. Krauss, 1984, J. Chem. Phys. 81, 6026-6033.
- A. Szabo, N.S. Ostlund, 1989, "Modern Quantum Chemistry: Introduction to Advanced Electronic Structure Theory". MacMillan Publishing Co., New York.
- W.R. Wadt, P.J. Hay, 1985, "Ab Initio effective core potentials for molecular calculations. Potentials for main group elements Na to Bi," J. Chem. Phys. 82, 284-298.
- N.M. Wallace, J.P. Blaudeau, R.M. Pitzer, 1991, "Optimized Gaussian Basis Sets for use with Relativistic Effective (core) Potentials: Li-Ar,"\ Int. J. Quantum Chem. (in press).
Contributors and Attributions
- Jan K. Labanowski, Ohio Supercomputer Center, 1224 Kinnear Rd., Columbus, | | OH 43212-1163, USA. E-mail: jkl@osc.edu, JKL@OHSTPY.BITNET

