6: Angular Momentum
- Page ID
- 8855
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Particle in a Ring
Consider a variant of the one-dimensional particle in a box problem in which the x-axis is bent into a ring of radius R. We can write the same Schrödinger equation
\[ \dfrac{-\hbar^2}{2m} \dfrac{d^2 \psi(x)}{dx^2} = E \psi(x) \label{1}\]
There are no boundary conditions in this case since the x-axis closes upon itself. A more appropriate independent variable for this problem is the angular position on the ring given by, \( \phi = x {/} R \) . The Schrödinger equation would then read
\[ -\dfrac{\hbar^2}{2mR^2} \dfrac{d^2 \psi (\phi)} {d (\phi)^2} = E \psi (\phi) \label{2}\]
The kinetic energy of a body rotating in the xy-plane can be expressed as
\[ E = \dfrac{L_z^2}{2I} \label{3}\]
where
\[I = mR^2\]
is the moment of inertia and \( L_z\), the z-component of angular momentum. (Since \( L = r \times p\), if r and p lie in the xy-plane, L points in the z-direction.) The structure of Equation \(\ref{2}\) suggests that this angular-momentum operator is given by
\[ \hat{L_z} = -{i} \hbar \dfrac{\partial}{\partial \phi} \label{4}\]
This result will follow from a more general derivation in the following Section. The Schrödinger equation (Equation \(\ref{2}\)) can now be written more compactly as
\[ \psi \prime \prime \ (\phi) + m^2 \psi (\phi) = 0 \label{5}\]
where
\[m^2 \equiv 2IE/ \hbar^2\label{6}\]
(Please do not confuse this variable m with the mass of the particle!) Possible solutions to (Equation \(\ref{5}\)) are
\[ \psi (\phi) = \text{const}\, e^{\pm{i}m\phi} \label{7}\]
For this wavefunction to be physically acceptable, it must be single-valued. Since \(\phi \) increased by any multiple of \(2\pi \) represents the same point on the ring, we must have
\[ \psi (\phi + 2\pi ) = \psi (\phi) \label{8}\]
and therefore
\[e^{{i}m (\phi + 2\pi)} = e^{{i}m \phi} \label{9}\]
This requires that
\[e^{2\pi {i}m} = 1 \label{10}\]
which is true only if \(m\) is an integer:
\[ m = 0, \pm 1, \pm 2... \label{11} \]
Using Equation \(\ref{6}\), this gives the quantized energy values
\[E_m = \dfrac{\hbar^2}{2I} m^2 \label{12}\]
In contrast to the particle in a box, the eigenfunctions corresponding to \(+m \) and \(-m \) (Equation \(\ref{7}\)) are linearly independent, so both must be accepted. Therefore all eigenvalues, except \(E_0 \), are two-fold (or doubly) degenerate. The eigenfunctions can all be written in the form const \( e^{{i}m \phi} \), with m allowed to take either positive and negative values (or 0), as in Equation \(\ref{10}\). The normalized eigenfunctions are
\[ {\psi _{m}} (\phi) = \dfrac{1}{\sqrt{2 \pi}} e^{im\phi} \label{13}\]
and can be verified to satisfy the normalization condition containing the complex conjugate
\[ \int\limits_{0}^{2\pi} {\psi_{m}^*} (\phi) {\psi _{m}} (\phi) d\phi = 1 \]
where we have noted that \( {\psi_{m}^*} (\phi) = (2\pi)^{-1/2} e^{-{i}m\phi} \). The mutual orthogonality of the functions (Equation \(\ref{13}\)) also follows easily, for
\[\int\limits_{0}^{2\pi} {\psi_{m^\prime}^*} {\psi _{m}} (\phi) d\phi = \dfrac{1}{2\pi} \int\limits_{0}^{2\pi} e^{{i}(m-m^\prime) \phi} d\phi \]
\[ = \dfrac{1}{2\pi} \int\limits_{0}^{2\pi} [cos(m-m^\prime)\phi + {i} sin(m-m^\prime)\phi] d\phi =0 \]
for \( m^\prime \neq m \).
The solutions in Equation \(\ref{12}\) are also eigenfunctions of the angular momentum operator (Equation \(\ref{4}\)), with
\[ \hat{L_z} \psi_{m} (\phi) = m\hbar \psi_{m} (\phi), m = 0, \pm 1, \pm 2...\]
This is a instance of a fundamental result in quantum mechanics, that any measured component of orbital angular momentum is restricted to integral multiples of \( \hbar \). The Bohr theory of the hydrogen atom, to be discussed in the next Chapter, can be derived from this principle alone.
Free Electron Model for Aromatic Molecules
The benzene molecule consists of a ring of six carbon atoms around which six delocalized pi-electrons can circulate. A variant of the FEM for rings predicts the ground-state electron configuration which we can write as \( 1\pi^{2} 2\pi^{4} \), as shown here:

The enhanced stability the benzene molecule can be attributed to the complete shells of \(\pi \)-electron orbitals, analogous to the way that noble gas electron configurations achieve their stability. Naphthalene, apart from the central C-C bond, can be modeled as a ring containing 10 electrons in the next closed-shell configuration\( 1\pi^{2} 2\pi^{4} 3\pi^{4} \). These molecules fulfill Hückel's "4N+2 rule" for aromatic stability. The molecules cyclobutadiene \( {(1\pi^{2} 2\pi^{2})} \) and cyclooctatetraene\( {(1\pi^{2} 2\pi^{4} 3\pi^{2})} \), even though they consist of rings with alternating single and double bonds, do not exhibit aromatic stability since they contain partially-filled orbitals.
The longest wavelength absorption in the benzene spectrum can be estimated according to this model as
\[ \dfrac{hc}{\lambda} = E_2 - E_1 = \dfrac{\hbar^2}{2mR^2} {(2^2 -1^2)} \]
The ring radius R can be approximated by the C-C distance in benzene, 1.39 Å. We predict \( \lambda \approx \) 210 nm, whereas the experimental absorption has \( \lambda_{max} \approx \) 268 nm.
Spherical Polar Coordinates
The motion of a free particle on the surface of a sphere will involve components of angular momentum in three-dimensional space. Spherical polar coordinates provide the most convenient description for this and related problems with spherical symmetry. The position of an arbitrary point r is described by three coordinates \( r , \theta, \phi \) as shown in Figure \(\PageIndex{2}\).
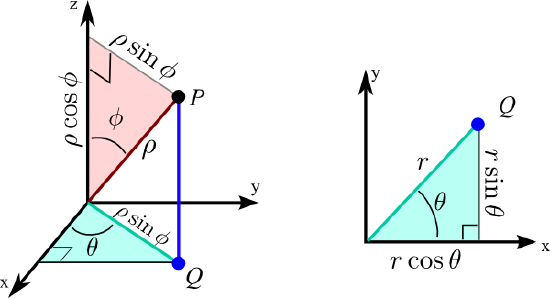
These are connected to Cartesian coordinates by the relations
\[ x = r \sin\theta \cos \phi \]
\[ y = r \sin \theta \sin \phi \]
\[ z = r \cos \theta \]
The radial variable r represents the distance from r to the origin, or the length of the vector r:
\[ r= \sqrt{x^2 +y^2 +z^2} \]
The coordinate \( \theta \) is the angle between the vector r and the z-axis, similar to latitude in geography, but with \( \theta= 0 \) and \( \theta = \pi \) corresponding to the North and South Poles, respectively. The angle \( \phi \) describes the rotation of r about the z-axis, running from 0 to \(2 \pi \), similar to geographic longitude. The volume element in spherical polar coordinates is given by
\[ d \tau = r^2 \sin \theta dr d \theta d\phi, \]
\[ r \in \{0, \infty \} , \theta \in \{0, \pi\}, \phi \in \{0, 2\pi \} \]
and represented graphically by the distorted cube in Figure \(\PageIndex{1}\).

Figure \(\PageIndex{3}\): Volume element in spherical polar coordinates. (CC BY; OpenStax).
We also require the Laplacian operator
\[ \nabla^{2} = \dfrac{1}{r^{2}} \dfrac{\partial}{\partial r} r^{2} \dfrac{\partial}{\partial r} + \dfrac{1}{r^2 sin \theta} \dfrac{\partial}{\partial \theta } sin \theta \dfrac{\partial}{\partial \theta } + \dfrac{1}{r^2 sin^2 \theta} \dfrac{\partial^2}{\partial \phi^2} \]
A detailed derivation is given in Supplement 6.
Rotation in Three Dimensions
A particle of mass M, free to move on the surface of a sphere of radius R, can be located by the two angular variables \( \theta, \phi \). The Schrödinger equation therefore has the form
\[ -\dfrac{\hbar^2}{2M} \nabla^{2} Y ({\theta , \phi}) = E Y ({\theta , \phi}) \]
with the wavefunction conventionally written as \(Y ({\theta , \phi}) \). These functions are known as spherical harmonics and have been used in applied mathematics long before quantum mechanics. Since \(r = R\), a constant, the first term in the Laplacian does not contribute. The Schrödinger equation reduces to
\[ \left\{ \dfrac{1}{sin \theta} \dfrac{\partial}{\partial \theta } sin \theta \dfrac{\partial}{\partial \theta } + \dfrac{1}{sin^2 \theta} \dfrac{\partial^2}{\partial \phi^2} + \lambda \right\} Y ({ \theta , \phi}) = 0 \]
where
\[ \lambda = \dfrac{2MR^2E}{\hbar^2} = \dfrac{2IE}{\hbar^2} \]
again introducing the moment of inertia \( I = MR^2 \). The variables \( \theta \) and \( \phi \) can be separated in Equation \(\ref{22}\) after multiplying through by \( sin^2 \theta \). If we write
\[ Y ({\theta , \phi }) = \Theta ({\theta }) \Phi ({\phi }) \]
and follow the procedure used for the three-dimensional box, we find that dependence on \(\phi \) alone occurs in the term
\[ \dfrac{\Phi^{\prime \prime} ({\phi)} }{\Phi ({\phi}) } = const \]
This is identical in form to Equation \(\ref{5}\), with the constant equal to \( -m^2 \), and we can write down the analogous solutions
\[ \Phi_{m}({\phi}) = \sqrt{\dfrac{1}{2 \pi}} e^{im \phi}, m=0, \pm 1, \pm 2 ... \]
Substituting Equation \(\ref{24}\) into Equation \(\ref{22}\) and cancelling the functions \( \Phi ({\phi }) \), we obtain an ordinary differential equation for \( \Theta ({\theta }) \)
\[ \left \{ \dfrac{1}{sin \theta} \dfrac{d}{d \theta} sin \theta \dfrac{d}{d \theta} - \dfrac{m^2}{sin^2 \theta} + \lambda \right \} \Theta ({\theta}) = 0 \]
Consulting our friendly neighborhood mathematician, we learn that the single-valued, finite solutions to (Equation \(\ref{27}\)) are known as associated Legendre functions. The parameters \( \lambda \) and \(m\) are restricted to the values
\[ \lambda = \ell ({ \ell + 1}) , \ell = 0, 1, 2 ... \]
while
\[ m = 0, \pm 1, \pm 2 ... \pm \ell ({2 \ell +1 values}) \]
Putting Equation \(\ref{28}\) into Equation \(\ref{23}\), the allowed energy levels for a particle on a sphere are found to be
\[ E_{\ell} = \dfrac{\hbar^2}{2I} \ell ({ \ell + 1}) \]
Since the energy is independent of the second quantum number m, the levels (Equation \(\ref{30}\)) are \( ({2 \ell+1}) \)-fold degenerate. The spherical harmonics constitute an orthonormal set satisfying the integral relations
\[ \int_0^{\pi} \int_0^{2 \pi} Y_{\ell^{\prime} m^{\prime}}^* ({ \theta , \phi }) Y_{\ell m} ({\theta , \phi}) sin \theta d \theta d \phi = \delta_{\ell \ell^{\prime}} \delta_{mm^{\prime}} \]
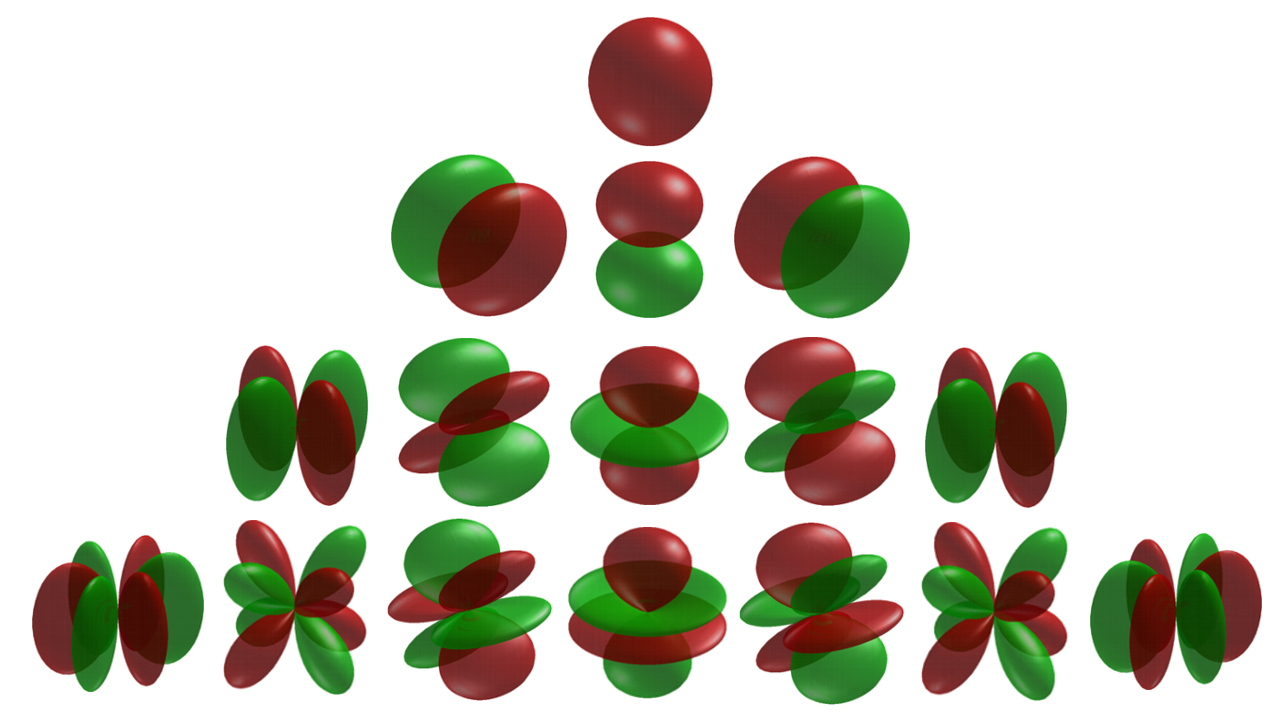
The following table lists the spherical harmonics through \( \ell \) = 2, which will be sufficient for our purposes.
\[ Spherical Harmonics Y_{\ell m} ({\theta , \phi}) \]
|
\[ Y_{00} = \left({\dfrac{1}{4 \pi}} \right)^{1/2} \] \[ Y_{10} = \left({\dfrac{3}{4 \pi}} \right)^{1/2} cos \theta \] \[ Y_{1 \pm 1} = \mp \left({\dfrac{3}{4 \pi}} \right)^{1/2} sin \theta e^{\pm i \phi} \] \[ Y_{20} = \left({\dfrac{5}{16 \pi}} \right)^{1/2} ({ 3 cos^2 \theta - 1}) \] \[ Y_{2 \pm 1} = \mp \left({\dfrac{15}{8 \pi}} \right)^{1/2} cos \theta sin \theta e^{\pm i \phi} \] \[ Y_{2 \pm 2} = \left({\dfrac{15}{32 \pi}} \right)^{1/2} sin^2 \theta e^{\pm 2i \phi} \] |
A graphical representation of these functions is given in Figure \(\PageIndex{4}\). Surfaces of constant absolute value are drawn, positive where green and negative where red.
Theory of Angular Momentum
Generalization of the energy-angular momentum relation in Equation \(\ref{3}\) to three dimensions gives
\[ E = \dfrac{L^2}{2I} \]
Thus from Equation \(\ref{21}\)-\(\ref{23}\) we can identify the operator for the square of total angular momentum
\[\hat{L^2} = -\hbar^2 \left\{ \dfrac{1}{sin \theta} \dfrac{\partial}{\partial \theta} sin \theta \dfrac{\partial}{\partial \theta} + \dfrac{1}{sin^2 \theta} \dfrac{\partial^{2}}{\partial \phi^{2}} \right\} \]
By Equations \(\ref{28}\) and \(\ref{29}\), the functions \( Y ({ \theta , \phi}) \) are simultaneous eigenfunctions of \( \hat{L^2} \) and \( \hat{L}_z \) such that
\[ \hat{L^2} Y_{\ell m} ({\theta , \phi}) = \ell ({\ell + 1}) \hbar^2 Y_{\ell m} ({\theta , \phi}) \]
and
\[ \hat{L}_z Y_{\ell m} ({\theta, \phi}) = m \hbar Y_{\ell m} ({\theta , \phi}) \]
But the \( Y_{\ell m} ({\theta , \phi}) \) are not eigenfunctions of either \( L_x \) and \(L_y \) (unless \(\ell \) = 0). Note that the magnitude of the total angular momentum \( \sqrt{\ell ({\ell +1}) } \hbar \) is greater than its maximum observable component in any direction, namely \(\ell \hbar \). The quantum-mechanical behavior of the angular momentum and its components can be represented by a vector model, illustrated in Figure 5. The angular momentum vector L, with magnitude \( \sqrt{\ell ({\ell +1}) } \hbar \), can be pictured as precessing about the z-axis, with its z-component \( L_z \) constant. The components \( L_x \) and \( L_y \) fluctuate in the course of precession, corresponding to the fact that the system is not in an eigenstate of either. There are 2\(\ell \) + 1 different allowed values for \( L_z \), with eigenvalues \( m \hbar ({ m = 0, \pm 1, \pm 2 ... \pm \ell }) \) equally spaced between \( + \ell \hbar \) and \( - \ell \hbar \).
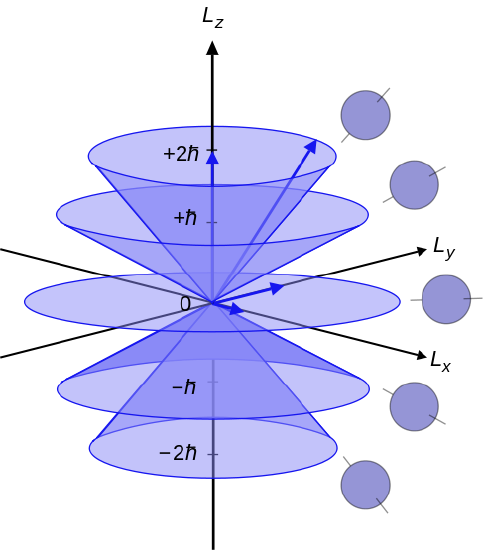
Figure \(\PageIndex{5}\): Vector model for angular momentum, showing the case \( \ell \)= 2. (Public Domain; Maschen).
This discreteness in the allowed directions of the angular momentum vector is called space quantization. The existence of simultaneous eigenstates of \( \hat{L^2} \) and any one component, conventionally \( \hat{L}_z \), is consistent with the commutation relations derived in Chap. 4:
\[ \left[ \hat{L}_x , \hat{L}_y \right] = i \hbar \hat{L}_z et cyc\]
and
\[ \left[ \hat{L^2} , \hat{L}_z \right] = 0 \]
Electron Spin
The electron, as well as certain other fundamental particles, possesses an intrinsic angular momentum or spin, in addition to its orbital angular momentum. These two types of angular momentum are analogous to the daily and annual motions, respectively, of the Earth around the Sun. To distinguish the spin angular momentum from the orbital, we designate the quantum numbers as s and \( m_s \), in place of \( \ell \) and m. For the electron, the quantum number s always has the value \( \dfrac{1}{2} \), while \(m_s \) can have one of two values,\( \pm \dfrac{1}{2} \). The electron is said to be an elementary particle of spin \( \dfrac{1}{2} \). The proton and neutron also have spin \( \dfrac{1}{2} \) and belong to the classification of particles called fermions, which are governed by the Pauli exclusion principle. Other particles, including the photon, have integer values of spin and are classified as bosons. These do not obey the Pauli principle, so that an arbitrary number can occupy the same quantum state. A complete theory of spin requires relativistic quantum mechanics. For our purposes, it is sufficient to recognize the two possible internal states of the electron, which can be called `spin up' and `spin down.' These are designated, respectively, by \( \alpha \) and \( \beta \) as factors in the electron wavefunction. Spins play an essential role in determining the possible electronic states of atoms and molecules.

