Chapter 2: Waves and Particles
- Page ID
- 8843
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Quantum mechanics is the theoretical framework which describes the behavior of matter on the atomic scale. It is the most successful quantitative theory in the history of science, having withstood thousands of experimental tests without a single verifiable exception. It has correctly predicted or explained phenomena in fields as diverse as chemistry, elementary-particle physics, solid-state electronics, molecular biology and cosmology. A host of modern technological marvels, including transistors, lasers, computers and nuclear reactors are offspring of the quantum theory. Possibly 30% of the US gross national product involves technology which is based on quantum mechanics. For all its relevance, the quantum world differs quite dramatically from the world of everyday experience. To understand the modern theory of matter, conceptual hurdles of both psychological and mathematical variety must be overcome. A paradox which stimulated the early development of the quantum theory concerned the indeterminate nature of light. Light usually behaves as a wave phenomenon but occasionally it betrays a particle-like aspect, a schizoid tendency known as the wave-particle duality. We consider first the wave theory of light.
The Double-Slit Experiment
Figure \(\PageIndex{1}\) shows a modernized version of the famous double-slit diffraction experiment first performed by Thomas Young in 1801. Light from a monochromatic (single wavelength) source passes through two narrow slits and is projected onto a screen. Each slit by itself would allow just a narrow band of light to illuminate the screen. But with both slits open, a beautiful interference pattern of alternating light and dark bands appears, with maximum intensity in the center. To understand what is happening, we review some key results about electromagnetic waves.

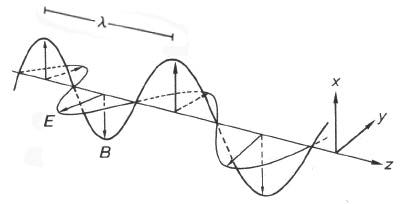
Maxwell's theory of electromagnetism was an elegant unification of the diverse phenomena of electricity, magnetism and radiation, including light. Electromagnetic radiation is carried by transverse waves of electric and magnetic fields, propagating in vacuum at a speed \( c≈3\times 10^8m/sec \), known as the "speed of light." As shown in Figure 2, the E and B fields oscillate sinusoidally, in synchrony with one another. The magnitudes of E and B are proportional (\(B=E/c\) in SI units). The distance between successive maxima (or minima) at a given instant of time is called the wavelength \(\lambda\). At every point in space, the fields also oscillate sinusoidally as functions of time. The number of oscillations per unit time is called the frequency \(\nu\). Since the field moves one wavelength in the time \(\lambda/c\), the wavelength, frequency and speed for any wave phenomenon are related by \[ \lambda\nu=c\label{1}\]
The energy density contained in an electromagnetic field, even a static one, is given by
\[\rho=\dfrac{1}{2}\left(\epsilon_{0}E^{2}+\dfrac{B^{2}}{\mu_{0}}\right)\label{3}\]
Note that both of the above energy quantities depend quadratically on the fields E and B. To discuss the diffraction experiments described above, it is useful to define the amplitude of an electromagnetic wave at each point in space and time r, t by the function
\[\Psi\left(\vec{r},t\right)=\sqrt{\epsilon_{0}}E\left(\vec{r},t\right)=\dfrac{B\left(\vec{r},t\right)}{\sqrt{\mu_{0}}}\label{4}\]
such that the intensity is given by
\[\rho\left(\vec{r},t\right)=[\Psi\left(\vec{r},t\right)]^2\label{5}\]
The function \(\Psi(\vec{r},t)\) will, in some later applications, have complex values. In such cases we generalize the definition of intensity to
\[\rho\left(\vec{r},t\right)=|\Psi\left(\vec{r},t\right)|^2=\Psi\left(\vec{r},t\right)^\ast\Psi\left(\vec{r},t\right)\label{6}\]
where \(\Psi\left(\vec{r},t\right)^\ast\) represents the complex conjugate of \(\Psi\left(\vec{r},t\right)\). In quantum mechanical applications, the function \(\Psi\) is known as the wavefunction.
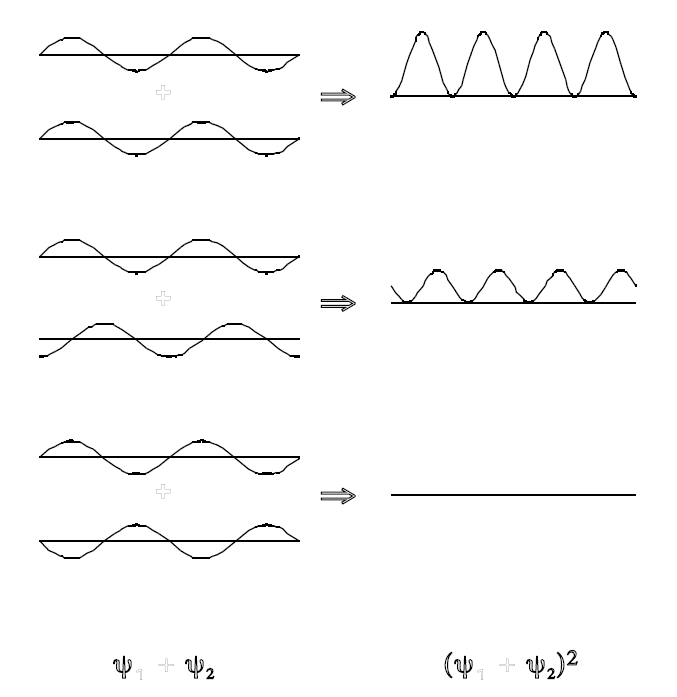
Figure \(\PageIndex{1}\): Interference of two equal sinusoidal waves. Top: constructive interference. Bottom: destructive interference. Center: intermediate case. The resulting intensities \(\rho=\Psi^2\) is shown on the right.
The electric and magnetic fields, hence the amplitude \(\Psi\), can have either positive and negative values at different points in space. In fact constructive and destructive interference arises from the superposition of waves, as illustrated in Figure \(\PageIndex{3}\). By Equation \(\ref{5}\), the intensity \(\rho\ge0\) everywhere. The light and dark bands on the screen are explained by constructive and destructive interference, respectively. The wavelike nature of light is convincingly demonstrated by the fact that the intensity with both slits open is not the sum of the individual intensities, ie, \(\rho\neq\rho_{1}+\rho_{2}\). Rather it is the wave amplitudes which add:
\[\Psi=\Psi_{1}+\Psi_{2}\label{7}\]
with the intensity given by the square of the amplitude:
\[\rho=\Psi^2=\Psi_{1}^2+\Psi_{2}^2+2\Psi_{1}\Psi_{2}\label{8}\]
The cross term \(2\Psi_{1}\Psi_{2}\) is responsible for the constructive and destructive interference. Where \(\Psi_{1}\) and \(\Psi_{2}\) have the same sign, constructive interference makes the total intensity greater than the the sum of \(\rho_{1}\) and \(\rho_{2}\). Where \(\Psi_{1}\) and \(\Psi_{2}\) have opposite signs, there is destructive interference. If, in fact, \(\Psi_{1}\) = \(-\Psi_{2}\) then the two waves cancel exactly, giving a dark fringe on the screen.
Wave-Particle Duality
The interference phenomena demonstrated by the work of Young, Fresnel and others in the early 19th Century, apparently settled the matter that light was a wave phenomenon, contrary to the views of Newton a century earlier--case closed! But nearly a century later, phenomena were discovered which could not be satisfactorily accounted for by the wave theory, specifically blackbody radiation and the photoelectric effect.
Deviating from the historical development, we will illustrate these effects by a modification of the double slit experiment. Let us equip the laser source with a dimmer switch capable of reducing the light intensity by several orders of magnitude, as shown in Figure \(\PageIndex{4}\). With each successive filter the diffraction pattern becomes dimmer and dimmer. Eventually we will begin to see localized scintillations at random positions on an otherwise dark screen. It is an almost inescapable conclusion that these scintillations are caused by photons, the bundles of light postulated by Planck and Einstein to explain blackbody radiation and the photoelectric effect.

But wonders do not cease even here. Even though the individual scintillations appear at random positions on the screen, their statistical behavior reproduces the original high-intensity diffraction pattern. Evidently the statistical behavior of the photons follows a predictable pattern, even though the behavior of individual photons is unpredictable. This implies that each individual photon, even though it behaves mostly like a particle, somehow carry with it a "knowledge" of the entire wavelike diffraction pattern. In some sense, a single photon must be able to go through both slits at the same time. This is what is known as the wave-particle duality for light: under appropriate circumstances light can behave as a wave or as a particle.
Planck's resolution of the problem of blackbody radiation and Einstein's explanation of the photoelectric effect can be summarized by a relation between the energy of a photon to its frequency:
\[E=h \nu \label{8b}\]
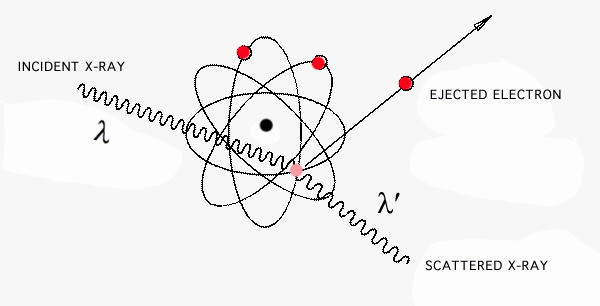
where \(h = 6.626\times 10^{-34} J sec\), known as Planck's constant. Much later, the Compton effect was discovered, wherein an x-ray or gamma ray photon ejects an electron from an atom, as shown in Figure \(\PageIndex{5}\). Assuming conservation of momentum in a photon-electron collision, the photon is found to carry a momentum p, given by
\[p=\dfrac{h}{\lambda} \label{9}\]
Equation \(\ref{8b}\) and \(\ref{9}\) constitute quantitative realizations of the wave-particle duality, each relating a particle-like property--energy or momentum--to a wavelike property--frequency or wavelength.
According to the special theory of relativity, the last two formulas are actually different facets of the same fundamental relationship. By Einstein's famous formula, the equivalence of mass and energy is given by
\[E=mc^2\label{10}\]
The photon's rest mass is zero, but in travelling at speed c, it acquires a finite mass. Equating Equation \(\ref{8}\)) and \(\ref{10}\) for the photon energy and taking the photon momentum to be \(p = mc\), we obtain
\[p = \dfrac{E}{c} = \dfrac{h\nu}{c} = \dfrac{h}{\lambda} \label{11}\]
Thus, the wavelength-frequency relation (Equation \(\ref{1}\)), implies the Compton-effect formula (Equation \(\ref{9}\)).
The best we can do is to describe the phenomena constituting the wave-particle duality. There is no widely accepted explanation in terms of everyday experience and common sense. Feynman referred to the "experiment with two holes" as the "central mystery of quantum mechanics." It should be mentioned that a number of models have been proposed over the years to rationalize these quantum mysteries. Bohm proposed that there might exist hidden variables which would make the behavior of each photon deterministic, ie, particle-like. Everett and Wheeler proposed the "many worlds interpretation of quantum mechanics" in which each random event causes the splitting of the entire universe into disconnected parallel universes in which each possibility becomes the reality. Needless to say, not many people are willing to accept such a metaphysically unwieldy view of reality. Most scientists are content to apply the highly successful computational mechanisms of quantum theory to their work, without worrying unduly about its philosophical underpinnings. Sort of like people who enjoy eating roast beef but would rather not think about where it comes from.
There was never any drawn-out controversy about whether electrons or any other constituents of matter were other than particle-like. Yet a variant of the double-slit experiment using electrons instead of light proves otherwise. The experiment is technically difficult but has been done. An electron gun, instead of a light source, produces a beam of electrons at a selected velocity, which is focused and guided by electric and magnetic fields. Then, everything that happens for photons has its analog for electrons. Individual electrons produce scintillations on a phosphor screen-this is how TV works. But electrons also exhibit diffraction effects, which indicates that they too have wavelike attributes. Diffraction experiments have been more recently carried out for particles as large as atoms and molecules, even for the C60 fullerene molecule.
De Broglie in 1924 first conjectured that matter might also exhibit a wave-particle duality. A wavelike aspect of the electron might, for example, be responsible for the discrete nature of Bohr orbits in the hydrogen atom. According to de Broglie's hypothesis, the "matter waves" associated with a particle have a wavelength given by
\[\lambda=h/p\label{12}\]
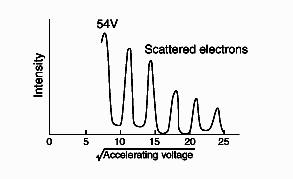
which is identical in form to Compton's result (Equation \ref{9}) (which, in fact, was discovered later). The correctness of de Broglie's conjecture was most dramatically confirmed by the observations of Davisson and Germer in 1927 of diffraction of monoenergetic beams of electrons by metal crystals, much like the diffraction of x-rays. And measurements showed that de Broglie's formula (Equation \(\ref{12}\)) did indeed give the correct wavelength (see Figure \(\PageIndex{6}\)).
The Schrödinger Equation
Schrödinger in 1926 first proposed an equation for de Broglie's matter waves. This equation cannot be derived from some other principle since it constitutes a fundamental law of nature. Its correctness can be judged only by its subsequent agreement with observed phenomena (a posteriori proof). Nonetheless, we will attempt a heuristic argument to make the result at least plausible. In classical electromagnetic theory, it follows from Maxwell's equations that each component of the electric and magnetic fields in vacuum is a solution of the wave equation
\[\nabla^2\Psi-\dfrac{1}{c^2}\dfrac{\partial ^2\Psi}{\partial t^2}=0\label{13}\]
where the Laplacian or "del-squared" operator is defined by
\[\nabla^2=\dfrac{\partial^2}{\partial x^2}+\dfrac{\partial^2}{\partial y^2}+\dfrac{\partial^2}{\partial z^2}\label{14}\]
We will attempt now to create an analogous equation for de Broglie's matter waves. Accordingly, let us consider a very general instance of wave motion propagating in the x-direction. At a given instant of time, the form of a wave might be represented by a function such as
\[\psi(x)=f\left(\dfrac {2\pi x}{ \lambda}\right)\label{15}\]
where \(f(\theta)\) represents a sinusoidal function such as \(\sin\theta\), \(\cos\theta\), \(e^{i\theta}\), \(e^{-i\theta}\) or some linear combination of these. The most suggestive form will turn out to be the complex exponential, which is related to the sine and cosine by Euler's formula
\[e^{i\theta}=\cos\theta + i \sin\theta\label{16}\]
Each of the above is a periodic function, its value repeating every time its argument increases by \(2\pi\). This happens whenever x increases by one wavelength \(\lambda\). At a fixed point in space, the time-dependence of the wave has an analogous structure:
\[T(t)=f(2\pi\nu t)\label{17}\]
where \(\nu\) gives the number of cycles of the wave per unit time. Taking into account both x- and t-dependence, we consider a wavefunction of the form
\[\Psi(x,t)=exp\left[2\pi i\left(\dfrac{x}{\lambda}-\nu t\right)\right]\label{18}\]
representing waves travelling from left to right. Now we make use of the Planck and de Broglie formulas (Equation \(\ref{8}\) and \(\ref{12}\), respectively) to replace \(\nu\) and \(\lambda\) by their particle analogs. This gives
\[\Psi(x,t)=exp[i(px-Et)/\hbar]\label{19}\]
where
\[\hbar\equiv\dfrac{h}{2\pi}\label{20}\]
Since Planck's constant occurs in most formulas with the denominator \(2\pi\), this symbol was introduced by Dirac. Now Equation \(\ref{17}\) represents in some way the wavelike nature of a particle with energy E and momentum p. The time derivative of Equation \ref{19} gives
\[\dfrac{\partial\Psi}{\partial t} = -(iE/\hbar)\times \exp \left[\dfrac{i(px-Et)}{\hbar} \right]\label{21}\]
Thus
\[i\hbar\dfrac{\partial\Psi}{\partial t} = E\Psi\label{22}\]
Analogously
\[-i\hbar\dfrac{\partial\Psi}{\partial x} = p\Psi\label{23}\]
and
\[-\hbar^2\dfrac{\partial^2\Psi}{\partial x^2} = p^2\Psi\label{24}\]
The energy and momentum for a nonrelativistic free particle are related by
\[E=\dfrac{1}{2}mv^2=\dfrac{p^2}{2m}\label{25}\]
Thus \(\Psi(x,t)\) satisfies the partial differential equation
\[i\hbar\dfrac{\partial\Psi}{\partial t}=-\dfrac{\hbar^2}{2m}\dfrac{\partial^2\Psi}{\partial x^2}\label{26}\]
For a particle with a potential energy \(V(x)\),
\[E=\dfrac{p^2}{2m}+V(x)\label{27}\]
we postulate that the equation for matter waves generalizes to
\[i\hbar\dfrac{\partial\Psi}{\partial t}=\left[-\dfrac{\hbar^2}{2m}\dfrac{\partial^2}{\partial x^2}+V(x)\right]\Psi\label{28}\]
For waves in three dimensions should then have
\[i\hbar\dfrac{\partial}{\partial t}\Psi(\vec{r},t)=\left[-\dfrac{\hbar^2}{2m}\nabla^2+V(\vec{r})\right]\Psi(\vec{r},t)\label{29}\]
Here the potential energy and the wavefunction depend on the three space coordinates x, y, z, which we write for brevity as r. This is the time-dependent Schrödinger equation for the amplitude \(\Psi(\vec{r}, t)\) of the matter waves associated with the particle. Its formulation in 1926 represents the starting point of modern quantum mechanics. (Heisenberg in 1925 proposed another version known as matrix mechanics.)
For conservative systems, in which the energy is a constant, we can separate out the time-dependent factor from (19) and write
\[\Psi(\vec{r},t)=\psi(\vec{r})e^{-iEt\div\hbar}\label{30}\]
where \(\psi(\vec{r})\) is a wavefunction dependent only on space coordinates. Putting Equation \ref{30} into Equation \ref{29} and cancelling the exponential factors, we obtain the time-independent Schrödinger equation:
\[\left[-\dfrac{\hbar^2}{2m}\nabla^2+V(\vec{r})\right]\psi(\vec{r})=E\psi(\vec{r})\label{31}\]
Most of our applications of quantum mechanics to chemistry will be based on this equation.
The bracketed object in Equation \(\ref{31}\) is called an operator. An operator is a generalization of the concept of a function. Whereas a function is a rule for turning one number into another, an operator is a rule for turning one function into another. The Laplacian (\(\nabla\)) is an example of an operator. We usually indicate that an object is an operator by placing a `hat' over it, eg, \(\hat{A}\). The action of an operator that turns the function f into the function g is represented by
\[\hat{A}f=g\label{32}\]
Equation \(\ref{23}\) implies that the operator for the x-component of momentum can be written
\[\hat{p}_{x}=-i\hbar\dfrac{\partial}{\partial x}\label{33}\]
and by analogy, we must have
\[\hat{p}_{y}=-i\hbar\dfrac{\partial}{\partial y}\]
and
\[\hat{p}_{z}=-i\hbar\dfrac{\partial}{\partial z}\label{34}\]
The energy, as in Equation \(\ref{27}\), expressed as a function of position and momentum is known in classical mechanics as the Hamiltonian. Generalizing to three dimensions,
\[\hat{H}=\dfrac{p^2}{2m}+V(\vec{r})=\dfrac{1}{2m}(p_{x}^2+p_{y}^2+p_{z}^2)+V(x,y,z)\label{35}\]
We construct thus the corresponding quantum-mechanical operator
\[\hat{H}=-\dfrac{\hbar^2}{2m}\left(\dfrac{\partial^2}{\partial x^2}+\dfrac{\partial^2}{\partial y^2}+\dfrac{\partial^2}{\partial z^2}\right)+V(x,y,z)=-\dfrac{\hbar^2}{2m}\nabla^2+V(\vec{r})\label{36}\]
The time-independent Schrödinger equation (Equation \(\ref{31}\)) can then be written symbolically as
\[\hat{H}\Psi=E\Psi\label{37}\]
This form is actually more generally to any quantum-mechanical problem, given the appropriate Hamiltonian and wavefunction. Most applications to chemistry involve systems containing many particles--electrons and nuclei. An operator equation of the form
\[\hat{A}\psi=const \psi\label{38}\]
is called an eigenvalue equation. Recall that, in general, an operator acting on a function gives another function (e.g., Equation \(\ref{32}\)). The special case (Equation \(\ref{38}\)) occurs when the second function is a multiple of the first. In this case, \(\psi\) is known as an eigenfunction and the constant is called an eigenvalue. (These terms are hybrids with German, the purely English equivalents being `characteristic function' and `characteristic value.') To every dynamical variable \(A\) in quantum mechanics, there corresponds an eigenvalue equation, usually written
\[\hat{A}\psi=a\psi \label{39}\]
The eigenvalues a represent the possible measured values of the variable \(A\). The Schrödinger Equation (\(\ref{37}\)) is the best known instance of an eigenvalue equation, with its eigenvalues corresponding to the allowed energy levels of the quantum system.
The Wavefunction
For a single-particle system, the wavefunction \(\Psi(\vec{r},t)\), or \(\psi(\vec{r})\) for the time-independent case, represents the amplitude of the still vaguely defined matter waves. The relationship between amplitude and intensity of electromagnetic waves we developed for Equation \(\ref{6}\) can be extended to matter waves.
The most commonly accepted interpretation of the wavefunction is due to Max Born (1926), according to which \(\rho(r)\), the square of the absolute value of \(\psi(r)\) is proportional to the probability density (probability per unit volume) that the particle will be found at the position r. Probability density is the three-dimensional analog of the diffraction pattern that appears on the two-dimensional screen in the double-slit diffraction experiment for electrons described in the preceding Section. In the latter case we had the relative probability a scintillation would appear at a given point on the screen. The function \(\rho(r)\) becomes equal, rather than just proportional to, the probability density when the wavefunction is normalized, that is,
\[\int|\psi(\vec{r})|^2d\tau=1\label{40}\]
This simply accounts for the fact that the total probability of finding the particle somewhere adds up to unity. The integration in Equation \(\ref{40}\) extends over all space and the symbol \(d\tau\) designates the appropriate volume element. For example, the volume differential in Cartesian coordinates, \(d\tau=dx\,dy\,dz\) is changed in spherical coordinates to \(d\tau=r^2sin\theta\, dr \,d\theta \, d\phi\). The physical significance of the wavefunctions makes certain demands on its mathematical behavior. The wavefunction must be a single-valued function of all its coordinates, since the probability density ought to be uniquely determined at each point in space.
Moreover, the wavefunction should be finite and continuous everywhere, since a physically-meaningful probability density must have the same attributes. The conditions that the wavefunction be single-valued, finite and continuous--in short, "well behaved"-- lead to restrictions on solutions of the Schrödinger equation such that only certain values of the energy and other dynamical variables are allowed. This is called quantization and is in the feature that gives quantum mechanics its name.
Contributors and Attributions
Seymour Blinder (Professor Emeritus of Chemistry and Physics at the University of Michigan, Ann Arbor)
- Kevin Olson, Hope College. Holland, MI.

