Chapter 1: Atoms and Photons: Origin of Quantum Theory
- Page ID
- 8842
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\(\newcommand{\ket}[1]{\left| #1 \right>} \)
\( \newcommand{\bra}[1]{\left< #1 \right|} \)
\( \newcommand{\braket}[2]{\left< #1 \vphantom{#2} \right| \left. #2 \vphantom{#1} \right>} \)
\( \newcommand{\qmvec}[1]{\mathbf{\vec{#1}}} \)
\( \newcommand{\op}[1]{\hat{\mathbf{#1}}}\)
\( \newcommand{\expect}[1]{\langle #1 \rangle}\)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Atomic and Subatomic Particles
The notion that the building blocks of matter are invisibly tiny particles called atoms is usually traced back to the Greek philosophers Leucippus of Miletus and Democritus of Abdera in the 5th Century BC. The English chemist John Dalton developed the atomic philosophy of the Greeks into a true scientific theory in the early years of the 19th Century. His treatise New System of Chemical Philosophy gave cogent phenomenological evidence for the existence of atoms and applied the atomic theory to chemistry, providing a physical picture of how elements combine to form compounds consistent with the laws of definite and multiple proportions. Table \(\PageIndex{1}\) summarizes some very early measurements (by Sir Humphrey Davy) on the relative proportions of nitrogen and oxygen in three gaseous compounds.
| Compound | Percent N | Percent O | Ratio |
|---|---|---|---|
| I | 29.50 | 70.50 | 0.418 |
| II | 44.05 | 55.95 | 0.787 |
| III | 63.30 | 36.70 | 1.725 |
We would now identify these compounds as NO2, NO and N2O, respectively. We see in data such as these a confirmation of Dalton's atomic theory: that compounds consist of atoms of their constituent elements combined in small whole number ratios. The mass ratios in Table \(\PageIndex{1}\) are, with modern accuracy, 0.438, 0.875 and 1.750.
After over 2000 years of speculation and reasoning from indirect evidence, it is now possible in a sense to actually see individual atoms, as shown for example in Figure \(\PageIndex{1}\). The word "atom" comes from the Greek atomos, meaning literally "indivisible." It became evident in the late 19th Century, however, that the atom was not truly the ultimate particle of matter. Michael Faraday's work had suggested the electrical nature of matter and the existence of subatomic particles. This became manifest with the discovery of radioactive decay by Henri Becquerel in 1896 the emission of alpha, beta and gamma particles from atoms. In 1897, J. J. Thompson identified the electron as a universal constituent of all atoms and showed that it carried a negative electrical charge, now designated -e.

To probe the interior of the atom, Ernest Rutherford in 1911 bombarded a thin sheet of gold with a stream of positively-charged alpha particles emitted by a radioactive source. Most of the high-energy alpha particles passed right through the gold foil, but a small number were strongly detected in a way that indicated the presence a small but massive positive charge in the center of the atom (Figure \(\PageIndex{2}\)). Rutherford proposed the nuclear model of the atom. As we now understand it, an electrically-neutral atom of atomic number Z consists of a nucleus of positive charge +Ze, containing almost the entire the mass of the atom, surrounded by Z electrons of very small mass, each carrying a charge -e. The simplest atom is hydrogen, with Z = 1, consisting of a single electron outside a single proton of charge +e.
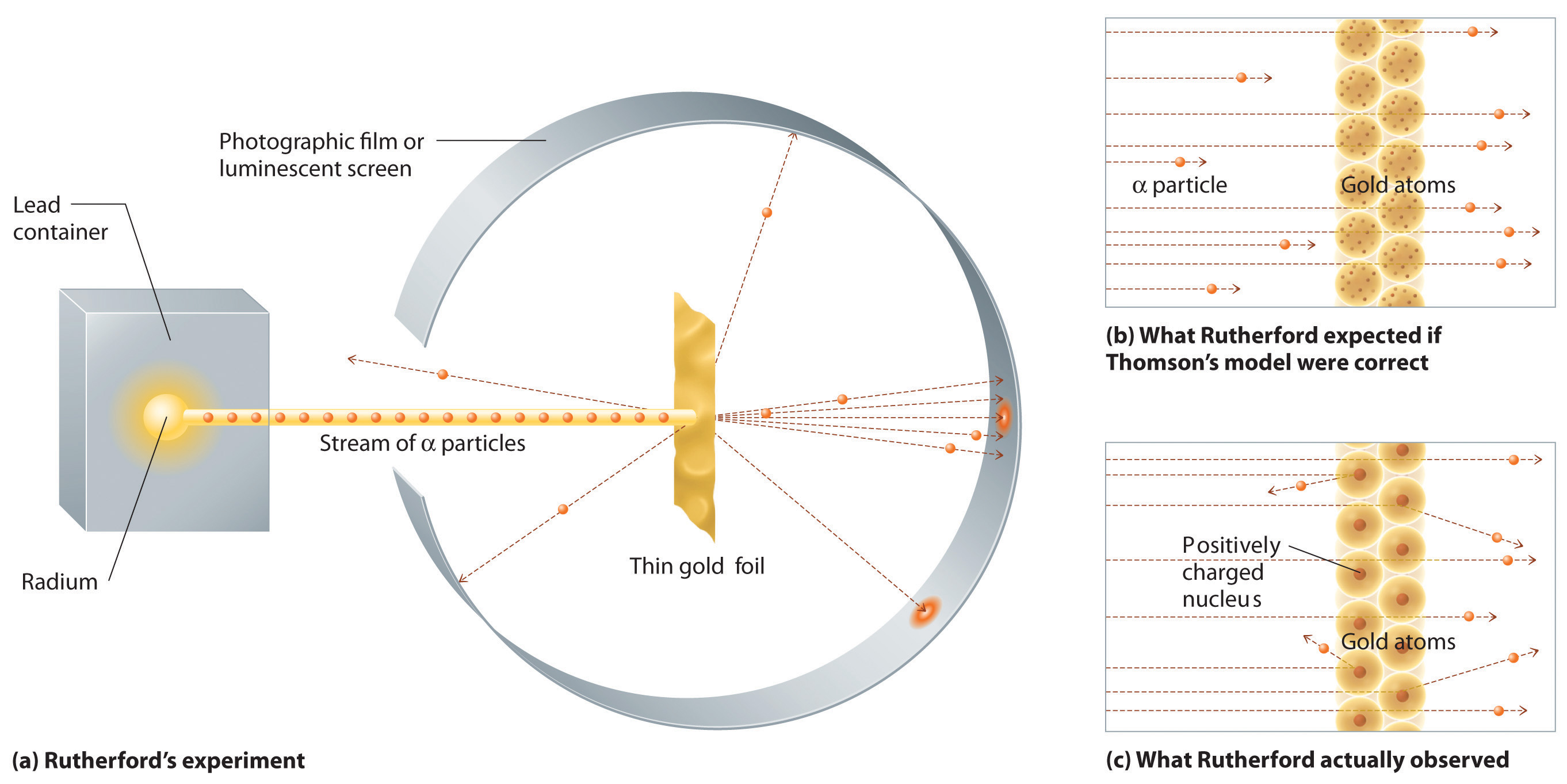
With the discovery of the neutron by Chadwick in 1932, the structure of the atomic nucleus was clarified. A nucleus of atomic number Z and mass number A was composed of Z protons and A-Z neutrons. Nuclei diameters are of the order of several times 10-15m. From the perspective of an atom, which is 105 times larger, a nucleus behaves, for most purposes, like a point charge +Ze.
During the 1960's, compelling evidence began to emerge that protons and neutrons themselves had composite structures, with major contributions by Murray Gell-Mann. According to the currently accepted "Standard Model," the protons and neutron are each made of three quarks, with compositions uud and udd, respectively. The up quark u has a charge of \( + \frac{2}{3}e \), while the down quark d has a charge of \( -\frac{1}{3}e \). Despite heroic experimental efforts, individual quarks have never been isolated, evidently placing them in the same category with magnetic monopoles. By contrast, the electron maintains its status as an indivisible elementary particle.
Electromagnetic Waves
Perhaps the greatest achievement of physics in the 19th century was James Clerk Maxwell's unification in 1864 of the phenomena of electricity, magnetism and optics. An (optional) summary of Maxwell's equations is given in Supplement 1A. Heinrich Hertz in 1887 was the first to demonstrate experimentally the production and detection of the electromagnetic waves predicted by Maxwell-specifically radio waves-by acceleration of electrical charges. As shown in Figure \(\PageIndex{3}\), electromagnetic waves consist of mutually perpendicular electric and magnetic fields, E and B respectively, oscillating in synchrony at high frequency and propagating in the direction of E x B.
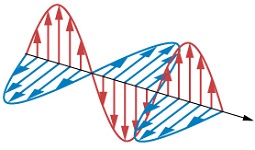
The wavelength \( \lambda \) is the distance between successive maxima of the electric (or magnetic) field. The frequency \( \nu \) represents the number of oscillations per second observed at a fixed point in space. The reciprocal of frequency \( \tau = \frac{1}{\nu} \) represents period of oscillation-the time it takes for one wavelength to pass a fixed point. The speed of propagation of the wave is therefore determined by \( \lambda = c \tau \) or in more familiar form
\[ \lambda \nu = c \label{1} \]
where \( c = 2.9979 \times 10^8m/sec\), usually called the speed of light, applies to all electromagnetic waves in vacuum. Frequencies are expressed in hertz (Hz), defined as the number of oscillations per second.
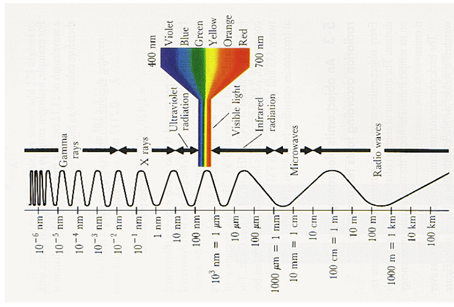
Electromagnetic radiation is now known to exist in an immense range of wavelengths including gamma rays, X-rays, ultraviolet, visible light, infrared, microwaves and radio waves, as shown in Figure \(\PageIndex{4}\).
Three Failures of Classical Physics
Isaac Newton's masterwork, Pincipia, published in 1687, can be considered to mark the beginning of modern physical science. Not only did Newton delineate the fundamental laws governing motion and gravitation but he established a general philosophical worldview which pervaded all scientific theories for two centuries afterwards. This system of thinking about the physical world is known as "Classical Physics." Its most notable feature is the primacy of cause and effect relationships. Given sufficient information about the present state of part of the Universe, it should be possible, at least in principle, to predict its future behavior (as well as its complete history.) This capability is known as determinism. For example, solar and lunar eclipses can be predicted centuries ahead, within an accuracy of several seconds. (But interestingly, we can't predict even a couple of days in advance if the weather will be clear enough to view the eclipse!) The other great pillar of classical physics is Maxwell's theory of electromagnetism.
The origin of quantum theory can be marked by three diverse phenomena involving electromagnetic radiation, which could not be adequately explained by the methods of classical physics. First among these was blackbody radiation, which led to the contribution of Max Planck in 1900. Next was the photoelectric effect, treated by Albert Einstein in 1905. Third was the origin of line spectra, the hero being Neils Bohr in 1913. A coherent formulation of quantum mechanics was eventually developed in 1925 and 1926, principally the work of Schrödinger, Heisenberg and Dirac. The remainder of this Chapter will describe the early contributions to the quantum theory by Planck, Einstein and Bohr.
Blackbody Radiation
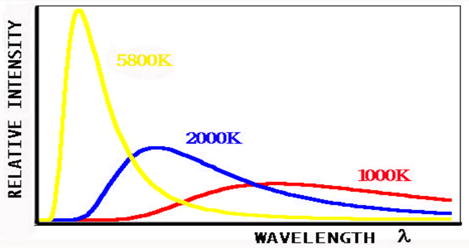
It is a matter of experience that a hot object can emit radiation. A piece of metal stuck into a flame can become "red hot." At higher temperatures, its glow can be described as "white hot." Under even more extreme thermal excitation it can emit predominantly blue light (completing a very patriotic sequence of colors!). Josiah Wedgwood, the famous pottery designer, noted as far back as 1782 that different materials become red hot at the same temperature. The quantitative relation between color and temperature is described by the blackbody radiation law. A blackbody is an idealized perfect absorber and emitter of all possible wavelengths \( \lambda\) of the radiation. Figure \(\PageIndex{5}\) shows experimental wavelength distributions of thermal radiation at several temperatures. Consistent with our experience, the maximum in the distribution, which determines the predominant color, increases with temperature. This relation is given by Wien's displacement law, which can be expressed
\[ T \lambda_{max} = 2.898 \times 10^6\, nm K\]
where the wavelength is expressed in nanometers (nm). At room temperature (300 K), the maximum occurs around 10\( \mu m\), in the infrared region. In Figure \(\PageIndex{5}\), the approximate values of \( \lambda_{max}\) are 2900 nm at 1000 K, 1450 nm at 2000 K and 500n m at 5800 K, the approximate surface temperature of the Sun. The Sun's \( \lambda_{max}\) is near the middle of the visible range (380-750nm) and is perceived by our eyes as white light.
The origin of blackbody radiation was a major challenge to 19th Century physics. Lord Rayleigh proposed that the electromagnetic field could be represented by a collection of oscillators of all possible frequencies. By simple geometry, the higher-frequency (lower wavelength) modes of oscillation are increasingly numerous since it it possible to fit their waves into an enclosure in a larger number of arrangements. In fact, the number of oscillators increases very rapidly as \( \lambda^{-4}\). Rayleigh assumed that every oscillator contributed equally to the radiation (the equipartition principle). This agrees fairly well with experiment at low frequencies. But if ultraviolet rays and higher frequencies were really produced in increasing number, we would get roasted like marshmallows by sitting in front of a fireplace! Fortunately, this doesn't happen, and the incorrect theory is said to suffer from an "ultraviolet catastrophe."
Max Planck in 1900 derived the correct form of the blackbody radiation law by introducing a bold postulate. He proposed that energies involved in absorption and emission of electromagnetic radiation did not belong to a continuum, as implied by Maxwell's theory, but were actually made up of discrete bundles which he called "quanta." Planck's idea is traditionally regarded as marking the birth of the quantum theory. A quantum associated with radiation of frequency \( \nu\) has the energy
\[ E = h \nu \label2\]
where the proportionality factor h = 6.626 x 10-34 J sec is known as Planck's constant. For our development of the quantum theory of atoms and molecules, we need only this simple result and do not have to follow the remainder of Planck's derivation. If you insist, however, the details are given in Supplement 1B.
The Photoelectric Effect
A familiar device in modern technology is the photocell or "electric eye," which runs a variety of useful gadgets, including automatic door openers. The principle involved in these devices is the photoelectric effect, which was first observed by Heinrich Hertz in the same laboratory in which he discovered electromagnetic waves. Visible or ultraviolet radiation impinging on clean metal surfaces can cause electrons to be ejected from the metal. Such an effect is not, in itself, inconsistent with classical theory since electromagnetic waves are known to carry energy and momentum. But the detailed behavior as a function of radiation frequency and intensity can not be explained classically.
The energy required to eject an electron from a metal is determined by its work function \( \Phi\). For example, sodium has \( \Phi = 1.82 eV\). The electron-volt is a convenient unit of energy on the atomic scale: 1 eV = 1.602 x 10-19J. This corresponds to the energy which an electron picks up when accelerated across a potential difference of 1 volt. The classical expectation would be that radiation of sufficient intensity should cause ejection of electrons from a metal surface, with their kinetic energies increasing with the radiation intensity. Moreover, a time delay would be expected between the absorption of radiation and the ejection of electrons. The experimental facts are quite different. It is found that no electrons are ejected, no matter how high the radiation intensity, unless the radiation frequency exceeds some threshold value \( \nu_{0}\) for each metal. For sodium \( \nu_{0}\) = 4.39 x 1014 Hz (corresponding to a wavelength of 683 nm), as shown in Figure \(\PageIndex{6}\). For frequencies \( \nu\) above the threshold, the ejected electrons acquire a kinetic energy given by
\[ \frac{1}{2}mv^{2} =h( \nu - \nu_{0}) =h \nu - \Phi \label3 \]
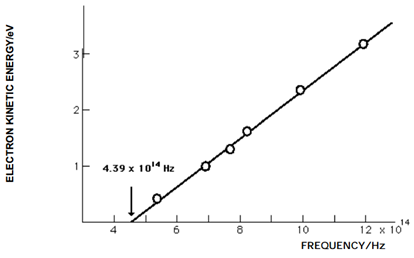
Evidently, the work function \( \Phi\) can be identified with \( h \nu_{0}\), equal to 3.65 x 10-19J=1.82 eV for sodium. The kinetic energy increases linearly with frequency above the threshold but is independent of the radiation intensity. Increased intensity does, however, increase the number of photoelectrons.
Einstein's explanation of the photoelectric effect in 1905 appears trivially simple once stated. He accepted Planck's hypothesis that a quantum of radiation carries an energy \( h \nu\). Thus, if an electron is bound in a metal with an energy \( \Phi\), a quantum of energy \( h \nu_{0}\) = \( \Phi\) will be sufficient to dislodge it. And any excess energy \( h( \nu - \nu_{0})\) will appear as kinetic energy of the ejected electron. Einstein believed that the radiation field actually did consist of quantized particles, which he named photons. Although Planck himself never believed that quanta were real, Einstein's success with the photoelectric effect greatly advanced the concept of energy quantization.
Line Spectra
Most of what is known about atomic (and molecular) structure and mechanics has been deduced from spectroscopy. Figure \(\PageIndex{7}\) shows two different types of spectra. A continuous spectrum can be produced by an incandescent solid or gas at high pressure. Blackbody radiation, for example, is a continuum. An emission spectrum can be produced by a gas at low pressure excited by heat or by collisions with electrons. An absorption spectrum results when light from a continuous source passes through a cooler gas, consisting of a series of dark lines characteristic of the composition of the gas. Frauenhofer between 1814 and 1823 discovered nearly 600 dark lines in the solar spectrum viewed at high resolution. It is now understood that these lines are caused by absorption by the outer layers of the Sun.
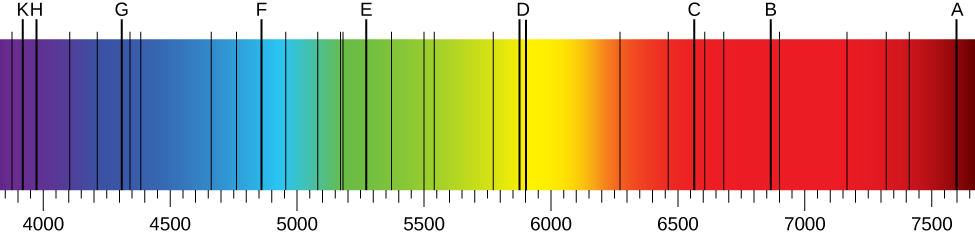


Gases heated to incandescence were found by Bunsen, Kirkhoff and others to emit light with a series of sharp wavelengths. The emitted light analyzed by a spectrometer (or even a simple prism) appears as a multitude of narrow bands of color. These so called line spectra are characteristic of the atomic composition of the gas. The line spectra of several elements are shown in Figure \(\PageIndex{8}\).

It is consistent with classical electromagnetic theory that motions of electrical charges within atoms can be associated with the absorption and emission of radiation. What is completely mysterious is how such radiation can occur for discrete frequencies, rather than as a continuum. The breakthrough that explained line spectra is credited to Neils Bohr in 1913. Building on the ideas of Planck and Einstein, Bohr postulated that the energy levels of atoms belong to a discrete set of values \( E_{n}\), rather than a continuum as in classical mechanics. When an atom makes a downward energy transition from a higher energy level \( E_{m}\) to a lower energy level \( E_{n}\), it caused the emission of a photon of energy
\[ h \nu =E_{m} - E_{n} \label{4}\]
This is what accounts for the discrete values of frequency \( \nu\) in emission spectra of atoms. Absorption spectra are correspondingly associated with the annihilation of a photon of the same energy and concomitant excitation of the atom from \( E_{n}\) to \( E_{m}\). Figure \(\PageIndex{9}\) is a schematic representation of the processes of absorption and emission of photons by atoms. Absorption and emission processes occur at the same set frequencies, as is shown by the two line spectra in Figure \(\PageIndex{7}\).

Rydberg (1890) found that all the lines of the atomic hydrogen spectrum could be fitted to a simple empirical formula
\[ \dfrac{1}{ \lambda} =R\left( \dfrac{1}{n_1^2} -\dfrac{1}{n_2^2}\right), n = 1,2,3..., n_2>n_1 \label{5} \]
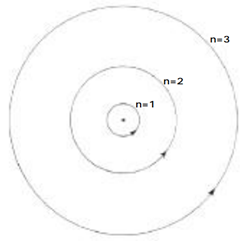
where R, known as the Rydberg constant, has the value 109,677 cm-1. This formula was found to be valid for hydrogen spectral lines in the infrared and ultraviolet regions, in addition to the four lines in the visible region. No analogously simple formula has been found for any atom other than hydrogen. Bohr proposed a model for the energy levels of a hydrogen atom which agreed with Rydberg's formula for radiative transition frequencies. Inspired by Rutherford's nuclear atom, Bohr suggested a planetary model for the hydrogen atom in which the electron goes around the proton in one of a set of allowed circular orbits, as shown in Fig 8. A more fundamental understanding of the discrete nature of orbits and energy levels had to await the discoveries of 1925-26, but Bohr's model provided an invaluable stepping-stone to the development of quantum mechanics. We will consider the hydrogen atom in greater detail in Chap. 7.

Contributors and Attributions
Seymour Blinder (Professor Emeritus of Chemistry and Physics at the University of Michigan, Ann Arbor)
- Cameron Holder, Hope College. Holland, MI.

