Enthalpy of Solution
- Page ID
- 1623
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)A solution is a homogeneous mixture of two or more substances and can either be in the gas phase, the liquid phase, the solid phase. The enthalpy change of solution refers to the amount of heat that is released or absorbed during the dissolving process (at constant pressure). This enthalpy of solution (\(ΔH_{solution}\)) can either be positive (endothermic) or negative (exothermic). When understanding the enthalpy of solution, it is easiest to think of a hypothetical three-step process happening between two substances. One substance is the solute, let’s call that A. The other substance is the solvent, let’s call that B.
Step 1: Breaking up the Solute
The first process that happens deals only with the solute, A, which requires breaking all intramolecular forces holding it together. This means the solute molecules separate from each other. The enthalpy of this process is called \(ΔH_1\). This since this is always an endothermic process (requiring energy to break interactions), then \(ΔH_1 > 0\).
\[ \ce{A (s) ->[\text{energy in}] A (g)} \nonumber \]
Step 2: Breaking up the Solvent
The second process is very similar to the first step. Much like how the solute, A, needed to break apart from itself, the solvent, B, also needs to overcome the intermolecular forces holding it together. This causes the solvent molecules separate from each other. The enthalpy of this process is called \(ΔH_2\). Like the first step, this reaction is always endothermic (\(ΔH_2 > 0\)) because energy is required to break the interaction between the B molecules.
\[ \ce{B (l) ->[\text{energy in}] B (g)} \nonumber \]
At this point, let us visualize what has happened so far. The solute, A, has broken from the intermolecular forces holding it together and the solvent, B, has broken from the intermolecular forces holding it together as well. It is at this time that the third process happens. We also have two values \(ΔH_1\) and \(ΔH_2\). that are both greater than zero (endothermic).
Step 3: Combining the Two Together
The third process is when substance A and substance B mix to for a solution. The separated solute molecules and the separated solvent molecules join together to form a solution. This solution will contain one mole of the solute A in an infinite amount of the solvent B.The enthalpy of combining these two substances to form the solution is \(ΔH_3\) and is an exothermic reaction (releasing heat since interactions are formed) with \(ΔH_3 < 0\).
\[ \ce{A (g) + B (g) ->[\text{energy out}] A(sol)} \nonumber \]
The enthalpy of solution can expressed as the sum of enthalpy changes for each step:
\[ΔH_{solution} = ΔH_1 + ΔH_2 + ΔH_3. \label{eq1}\]
So the enthalpy of solution can either be endothermic, exothermic or neither \(ΔH_{solution} = 0\)), depending on how much heat is required or release in each step. If \(ΔH_{solution} = 0\), then the solution is called an ideal solution and if \(ΔH_{solution} > 0\) or \(ΔH_{solution} < 0\), then these solutions are called non-ideal solutions.
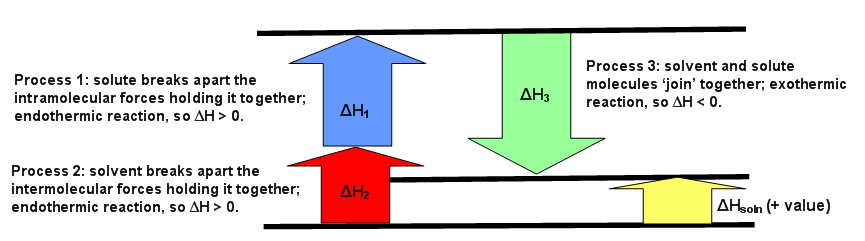
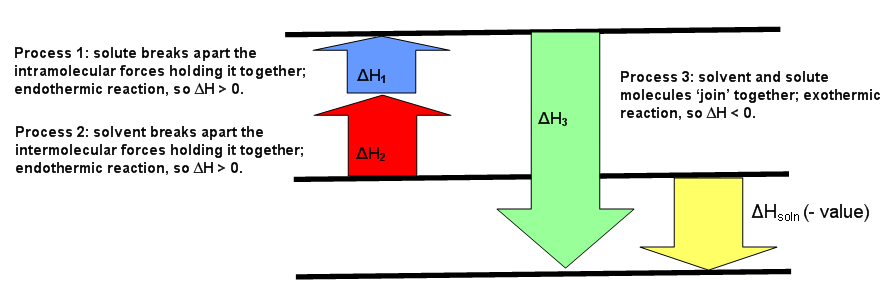
The diagrams below can be used as visuals to help facilitate the understanding of this concept. Figure \(\PageIndex{1}\) is for an endothermic reaction, where \(ΔH_{solution} > 0.\) Figure \(\PageIndex{2}\) is for an exothermic reaction, where \(ΔH_{solution} < 0\). Figure \(\PageIndex{3}\) is for an ideal solution, where \(ΔH_{solution} = 0\).
Ideal Solutions
The enthalpy of solution depends on the strengths of intermolecular forces of the solute and solvent and solvent (Equation \ref{eq1}). If the solution is ideal, and \(ΔH_{solution} = 0\), then
\[\begin{align*} ΔH_{solution} = ΔH_1 + ΔH_2 + ΔH_3 &= 0. \label{eq2} \\[4pt] ΔH_1 + ΔH_2 &= - ΔH_3 \end{align*}\]
This means the forces of attraction between like (the solute-solute and the solvent-solvent) and unlike (solute-solvent) molecules are the same (Figure \(\PageIndex{3}\)). If the solution is non-ideal, then either \(ΔH_1\) added to \(ΔH_2\) is greater than \(ΔH_3\) or \(ΔH_3\) is greater than the sum of \(ΔH_1\) and \(ΔH_2\). The first case means the forces of attraction of unlike molecules is greater than the forces of attraction between like molecules. The second case means the forces of attraction between like molecules is greater than the forces of attraction between unlike molecules (Figure \(\PageIndex{2}\)).
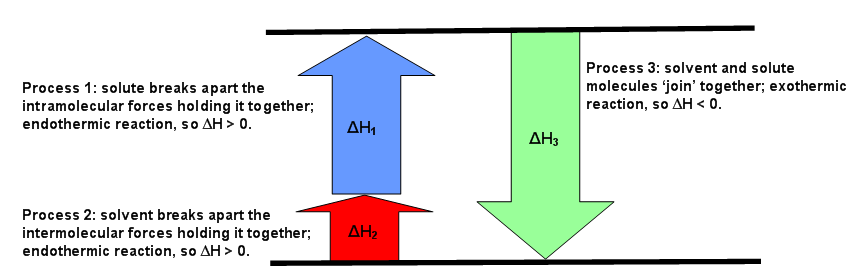
Table salt (\(\ce{NaCl}\)) dissolves readily in water. In solid (\(\ce{NaCl}\)), the positive sodium ions are attracted to the negative chloride ions. The same is true of the solvent, water; the partially positive hydrogen atoms are attracted to the partially negative oxygen atoms. While (\(\ce{NaCl}\)) dissolves in water, the positive sodium cations and chloride anions are stabilized by the water molecule electric dipoles. Thus, the intermolecular interactions (i.e., ionic bonds) between (\(\ce{NaCl}\)) are broken and the salt is dissolved. The overall chemical equation for this reaction is as follows:
\[\ce{NaCl (s) ->[H_2O] Na^+ (aq) + Cl^- (aq)}\]
Enthalpy of solution is only one part of the driving force in the formation of solutions; the other part is the entropy of solution.
References
- Petrucci, Harwood, Herring, Madura. General Chemistry: Principles & Modern Applications, Ninth Ed. Upper Saddle River, NJ: Pearson Education, Inc., 2007.
- McMurray, Fay. Chemistry, Third Ed. Upper Sadle River, NJ: Prentice-Hall, Inc., 2001.
Contributors and Attributions
- Zafir Javeed, Mark Tye (DVC)

