2.1.6: Stopped Flow
- Page ID
- 1432
The stopped-flow technique allows for the evaluation of solution-based kinetics on a milliseconds timescale with a very small volume of reactants used.
Introduction
Imagine you wanted to compute the initial rate of a reaction, one that, when the reactants combined changed color or fluoresced, however the reaction was far too fast to detect via the human eye alone. How would you go about determining the reaction rate? Could you use the continuous flow technique? But what if you only had a limited volume of the reactants at your disposal? The continuous flow technique requires that you have enough of the reactants to constantly flow through the spectrophotometer at a continuous rate. In cases like this, the Stopped Flow technique is probably more appropriate. Stopped-Flow allows for the rate of a solution-based reaction to be determined in milliseconds, and with a very small volume of reactants.
Mechanism
This technique involves two reactants held in separate reservoirs that are prevented from freely flowing by syringe pumps. The reaction is initiated by depressing the reactant syringes, and thus releasing the reactants into the connecting "mixing chamber" where the solutions are mixed. The reaction is monitored by observing the change in absorbance of the reaction solution as a function of time. As the reaction progresses it fills the “stop syringe” which then expands until it hits a block at the point when the reaction has reached a continuous flow rate, thereby stopping the flow and the reaction, and thus allowing the researcher to calculate the exact initial rate of reaction. See Figure 1 below:
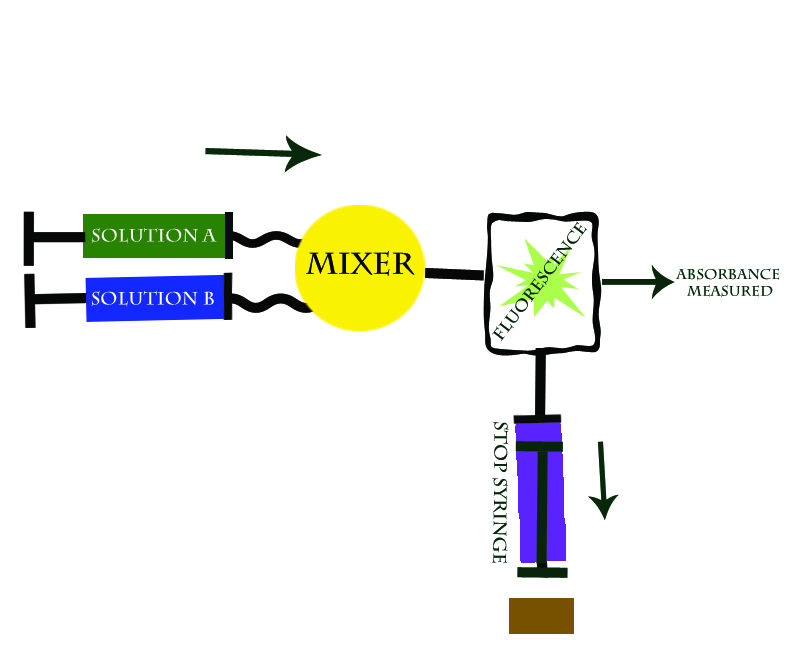
The Stopped Flow technique works because within milliseconds of combining the two reactants the absorbance can be read. In addition, the stop syringe assures for a steady rate of flow pas the spectophotometer so that reactants are being added to solution and forming products at a consistant rate.
Imagine a reaction that proceeds as follows:
\[A + B \rightarrow C + D \nonumber \]
Substance C is the product and Substance D is known to fluoresce. The optical path is 1 cm and the e value is 1 L/mol cm-1. Based on the following data gathered by the Stopped Flow method, determine the rate constant and the order of the reaction.
|
Time (seconds) |
Absorbance |
|
.001 |
.2 |
|
.002 |
.4 |
|
.003 |
.6 |
|
.004 |
.8 |
|
.005 |
1 |
|
.006 |
1.2 |
|
.007 |
1.4 |
|
.008 |
1.6 |
|
.009 |
1.8 |
(Hint: Make a graph and use that to find the order and the rate. If you need more help, these pages might help: Beer's Law and Reaction Rate)
Solution
This is a zero order reaction with a rate constant of 200 M/S.
We know that the absorbance is proportional to the change of the concentration of D over time because D fluoresces. However, from the reaction above, the concentration of C=D because the stoichiometry is 1:1.
Now lets start with the relationship between absorbance and concentration. From Beer's Law we know that absorbance is directly proportional to concentration, therefore we know, in this case, absorbance is equal to concentration because we divide by 1 and 1 (A = ε l c).
Now for the reaction rate and the reaction order. You can figure the order out by graphing the either concentration by time, ln(concentration) by time, or 1/concentration by time depending on the order of the reaction. If concentration by time is linear, then the reaction is zero order. If ln(concentration) by time is linear, then the reaction is first order. Finally, if 1/concentration by time is linear, then the reaction is 2nd order. Once you have determined that this reaction is zero order, you can find the slope of the line to solve for \(k\), and the rate of the reaction.
Resources
- Drobny, Engel, Philip Reid. Physical Chemistry for the Life Sciences. Pearson Education Inc., 2008. (344-345, 356-357).
- IUPAC. Compendium of Chemical Terminology, 2nd ed. (the "Gold Book"). Compiled by A. D. McNaught and A. Wilkinson. Blackwell Scientific Publications, Oxford (1997). XML on-line corrected version: goldbook.iupac.org (2006-) created by M. Nic, J. Jirat, B. Kosata; updates compiled by A. Jenkins. ISBN 0-9678550-9-8. doi:10.1351/goldbook.
- Lehrer, Sam. "Stopped Flow Kinnetics." Boston Biomedical Research Institute. BBRI, n.d. Web. 14 Mar 2011. http://www.bbri.org/index.php/stopped_flow_kin.html.
Contributors and Attributions
- Tammy Nguyen, Rachel Pruitt

